💯 博客内容：【数据结构】向上调整建堆和向下调整建堆的天壤之别以及堆排序算法

😀 作者：陈大大陈

🚀 个人简介：一个正在努力学技术的准前端，专注基础和实战分享，欢迎私信！

💖 欢迎大家：这里是CSDN，我总结知识和写笔记的地方，喜欢的话请三连，有问题请私信 😘 😘 😘

向上调整

向上调整建堆

向下调整

向下调整建堆

两种方法的天壤之别

总结一下

堆排序

向上调整

void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){	Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}

向上调整建堆

	for (int i = 1; i < n; i++){AdjustUp(a, i);}

向下调整

void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child+1< n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}

向下调整建堆

for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}

两种方法的天壤之别

这两个建堆方法看似相同，实际却有着天壤之别。

具体的数值我们可以计算一下。

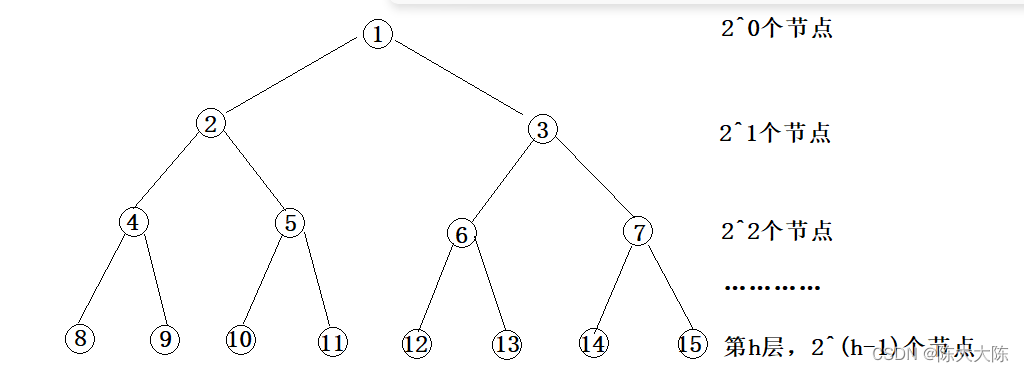
如图，二叉树的第h层有2^(h-1)个节点。

向下调整建堆最坏的情况就是每个节点都需要调整。

第一层有1个节点，最坏的情况是每个节点向下移动n-1层，次数就是1*(n-1)次。

第二层有2个节点，最坏的情况是每个节点向下移动n-2层，次数就是2*(n-2)次。

以此类推。。。

第n-2层有2^(n-3)个节点，最坏的情况是每个节点向下移动两层，次数就是2^(n-3)次.

第n-1层有2^(n-2)个节点，最坏的情况是每个节点向下移动一层，次数就是2^(n-2)次。

总共的计算次数就是f(h)=2^0*(n-1)+2^1*(n-2)+……+2^(h-3)*2+2*(n-2)*1次

这个数字我们可以用错位相减法计算出来。

最后得到的结果F(h）= 2^h -1 - h。

假设树的节点有N个。

那么根据公式，2 ^ h - 1= N。

把表达式往N上凑。

就得到F(N) = N - log(N+1)。

向下调整建堆的时间复杂度也就得出来了，log(N+1)的大小基本可忽略。

所以向下调整的时间复杂度是o(N)左右。

再来看向上调整建堆。

向上调整就没有这么优秀了。

假设树的高度是h,二叉树的最后一层就占了一半的节点。

我们仍旧按最坏的情况来算。

最后一层的每个节点都需要向上调整h-1次，光最后一层调整的次数就已经有2^(h-1)*(h-1)次了。

光看这一层可以看出差距。

上一条讲的向下调整的特点是节点多的层级调整的次数少，是少乘多。

而现在讲的向上调整恰恰相反。

节点多的层级调整的次数多，是多乘多，这就造成了时间复杂度的巨大差异。

同样来计算一下。

假设高度为h。

F(h)=2^1*1+2^2*2+……+2^(h-2)*h-2+2^(h-1)*(h-1)

同样使用错位相减，解得F(h) = 2^h * (h-2) + 2

因为 N = 2^h-1。

我们将F(h)换成关于N的式子，F(N) = (N+1) * (log(N+1) -2 ) + 2 。

同样是忽略掉不重要的数据，它的时间复杂度大概是O(N*logN)。它的量级比向下调整大了很多。

所以一般情况下，我们建堆一般是用向下调整。

总结一下

建堆——向下调整建堆——时间复杂度：O(N)

建堆——向上调整建堆——时间复杂度：O(N*logN)

时间复杂度上向下调整建堆优秀很多，我们建堆一般就使用它。

堆排序

void HeapSort(int* a, int n)
{、//向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}
//向下排序while (end>0){Swap(&a[0], &a[end]);AdjustDown(a,end, 0);--end;}
}