〇、推荐

无意中发现了一个巨牛的人工智能教程，忍不住分享一下给大家。教程不仅是零基础，通俗易懂，而且非常风趣幽默，像看小说一样！觉得太牛了，所以分享给大家。点这里可以跳转到教程。

一、简介

今天来学习下机器学习的敲门砖——感知机模型。网上查了很多中英文资料，得知感知机是在1957年由Frank Rosenblatt提出的，它被成为机器学习领域最为基础的模型。虽然是最为基础的，但是它在机器学习的领域中，有着举足轻重的地位，它是SVM（支持向量机）和NN（神经网络）学习的基础，可以说它是最古老的分类方法之一了。

虽然今天看来它的分类模型在大多数时候泛化能力不强，但是它的原理却值得好好研究。如果研究透了感知机模型，再学习支持向量机、神经网络，也是一个很好的起点。

感知机的思想很好理解，比如我们在一个屋子里有很多的男人和女人，感知机的模型就是尝试找到一条直线，能够把所有的男人和女人隔离开。放到三维或者更高维的空间，感知机的模型就是尝试找到一个超平面，能够把所有的二元类别隔离开。当然，如果我们找不到这么一条直线的话怎么办？找不到的话那就意味着类别线性不可分，也就意味着感知机模型不适合你的数据的分类。

所以，使用感知机一个最大的前提，就是数据是线性可分的，这严重限制了感知机的使用场景。它的分类竞争对手在面对不可分的情况时，比如支持向量机可以通过核技巧来让数据在高维可分，神经网络可以通过优化激活函数、增加隐藏层和支持多输出，来让数据可分。

感知机适用于具有线性可分的数据集的二分类问题，可以说是很局限了。它本质上是一个分离超平面。在向量维数（特征数）过高时，选择对偶形式算法。在向量个数（样本数）过多时，应选择原始算法。（什么是对偶形式算法，什么是原始算法，我会在后面讲）

二、模型

输入空间： X⊆Rn
输出空间 ：Y⊆−1,+1
假设空间 ：F⊆f|f(x)=ω⋅x+b
参数：ω∈Rn,b∈R
模型：f(x)=sign(ω⋅x+b)
符号函数为：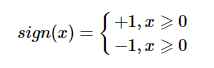
线性方程：ω⋅x+b 可以表示为特征空间 Rn中的一个分离超平面
损失函数是关于w,b的函数，将损失函数极小化(极小化即求极小值)的过程就是求w,b的过程，而损失函数的一个自然选择是误分类的总数(自然选择就是最接近人类思维方向逻辑推断)，但这样的话损失函数就不是w,b的连续可导函数。这儿为什么要求损失函数是关于w,b的连续可导函数，因为只有函数是连续可导的，我们才能方便的在该函数上确定极大值或极小值。

三、感知机算法的原始形式

1、理论

算法的输入为m个样本，每个样本对应于n维特征和一个二元类别输出1或者-1，如下：

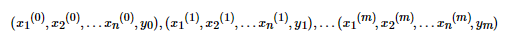
输出为分离超平面的模型系数θθ向量

算法的执行步骤如下：

1. 定义所有x0为1。选择θ向量的初值和 步长α的初值。可以将θ向量置为0向量，步长设置为1。要注意的是，由于感知机的解不唯一，使用的这两个初值会影响θ向量的最终迭代结果。
2. 在训练集里面选择一个误分类的点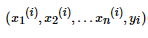, 用向量表示即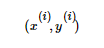，这个点应该满足：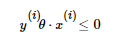
3. 对θ向量进行一次随机梯度下降的迭代：
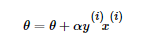
4. 检查训练集里是否还有误分类的点，如果没有，算法结束，此时的θ向量即为最终结果。如果有，继续第2步。

2、实现

from random import randint
import numpy as np
import matplotlib.pyplot as pltclass TrainDataLoader:def __init__(self):passdef GenerateRandomData(self, count, gradient, offset):x1 = np.linspace(1, 5, count)x2 = gradient*x1 + np.random.randint(-10,10,*x1.shape)+offsetdataset = []y = []for i in range(*x1.shape):dataset.append([x1[i], x2[i]])real_value = gradient*x1[i]+offsetif real_value > x2[i]:y.append(-1)else:y.append(1)return x1,x2,np.mat(y),np.mat(dataset)class SimplePerceptron:def __init__(self, train_data = [], real_result = [], eta = 1):self.w   =   np.zeros([1, len(train_data.T)], int)self.b   =   0self.eta =   etaself.train_data   = train_dataself.real_result  = real_resultdef nomalize(self, x):if x > 0 :return 1else :return -1def model(self, x):# Here are matrix dot multiply get one valuey = np.dot(x, self.w.T) + self.b# Use sign to nomalize the resultpredict_v = self.nomalize(y)return predict_v, ydef update(self, x, y):# w = w + n*y_i*x_iself.w = self.w + self.eta*y*x# b = b + n*y_iself.b = self.b + self.eta*ydef loss(slef, fx, y):return fx.astype(int)*ydef train(self, count):update_count = 0while count > 0:# count--count = count - 1if len(self.train_data) <= 0:print("exception exit")break# random select one train dataindex = randint(0,len(self.train_data)-1)x = self.train_data[index]y = self.real_result.T[index]# wx+bpredict_v, linear_y_v = self.model(x)# y_i*(wx+b) > 0, the classify is correct, else it's errorif self.loss(y, linear_y_v) > 0:continueupdate_count = update_count + 1self.update(x, y)print("update count: ", update_count)passdef verify(self, verify_data, verify_result):size = len(verify_data)failed_count = 0if size <= 0:passfor i in range(size):x = verify_data[i]y = verify_result.T[i]if self.loss(y, self.model(x)[1]) > 0:continuefailed_count = failed_count + 1success_rate = (1.0 - (float(failed_count)/size))*100print("Success Rate: ", success_rate, "%")print("All input: ", size, " failed_count: ", failed_count)def predict(self, predict_data):size = len(predict_data)result = []if size <= 0:passfor i in range(size):x = verify_data[i]y = verify_result.T[i]result.append(self.model(x)[0])return resultif __name__ == "__main__":# Init some parametersgradient = 2offset   = 10point_num = 1000train_num = 50000loader = TrainDataLoader()x, y, result, train_data =  loader.GenerateRandomData(point_num, gradient, offset)x_t, y_t, test_real_result, test_data =  loader.GenerateRandomData(100, gradient, offset)# First trainingperceptron = SimplePerceptron(train_data, result)perceptron.train(train_num)perceptron.verify(test_data, test_real_result)print("T1: w:", perceptron.w," b:", perceptron.b)# Draw the figure# 1. draw the (x,y) pointsplt.plot(x, y, "*", color='gray')plt.plot(x_t, y_t, "+")# 2. draw y=gradient*x+offset lineplt.plot(x,x.dot(gradient)+offset, color="red")# 3. draw the line w_1*x_1 + w_2*x_2 + b = 0plt.plot(x, -(x.dot(float(perceptron.w.T[0]))+float(perceptron.b))/float(perceptron.w.T[1]), color='green')plt.show()

3、效果

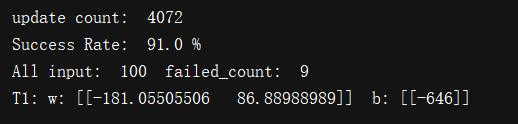
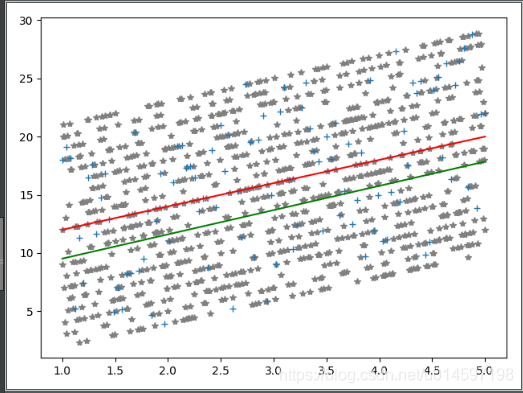
其中红色直线为实际的分类模型，绿色直线为通过训练数据训练后得到的模型，灰色’*’符号组成的点集为训练数据集，蓝色的’+’号组成的点集为验证数据集。

四、感知机算法的对偶形式

1、理论

对偶形式是对算法执行速度的优化。具体是怎么优化的呢？
通过上一节感知机模型的算法原始形式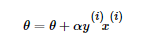可以看出，我们每次梯度的迭代都是选择的一个样本来更新θ向量，最终经过若干次的迭代得到最终的结果。对于从来都没有误分类过的样本，他被选择参与θ迭代的次数是0，对于被多次误分类而更新的样本j，它参与θ迭代的次数我们设置为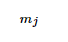。如果令θ向量初始值为0向量， 这样我们的θθ向量的表达式可以写为：

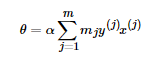
其中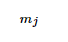为样本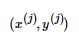在随机梯度下降到当前的这一步之前因误分类而更新的次数。

每一个样本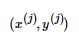的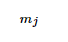的初始值为0，每当此样本在某一次梯度下降迭代中因误分类而更新时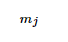，的值加1。

由于步长α为常量，我们令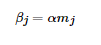,这样θ向量的表达式为:

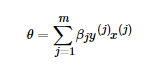
在每一步判断误分类条件的地方，我们用 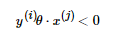的变种 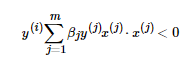来判断误分类。注意到这个判断误分类的形式里面是计算两个样本x(i)和x(j)x(i)和x(j)的内积，而且这个内积计算的结果在下面的迭代次数中可以重用。如果我们事先用矩阵运算计算出所有的样本之间的内积，那么在算法运行时， 仅仅一次的矩阵内积运算比多次的循环计算省时。 计算量最大的判断误分类这儿就省下了很多的时间，，这也是对偶形式的感知机模型比原始形式优的原因。

样本的内积矩阵称为Gram矩阵，它是一个对称矩阵，记为
这里给出感知机模型的算法对偶形式的内容。

算法的输入为m个样本，每个样本对应于n维特征和一个二元类别输出1或者-1，如下：

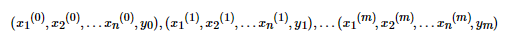
输出为分离超平面的模型系数θ向量

算法的执行步骤如下：

1. 定义所有x0为1，步长α初值，设置β的初值0。可以将α设置为1。要注意的是，由于感知机的解不唯一，使用的步长初值会影响θ向量的最终迭代结果。

2. 计算所有样本内积形成的Gram矩阵G。

3. 在训练集里面选择一个误分类的点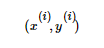，这个点应该满足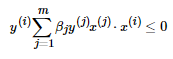： ， 在检查是否满足时可以通过查询Gram矩阵的gij 的值来快速计算是否小于0。

4. 对β向量的第i个分量进行一次更新：βi=βi+α

5. 检查训练集里是否还有误分类的点，如果没有，算法结束，此时的θθ向量最终结果为下式。如果有，继续第2步
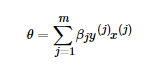   , 其中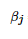 为β向量的第j个分量。

2、实现

# Init the parameter
from random import randint
import numpy as np
import matplotlib.pyplot as pltclass TrainDataLoader:def __init__(self):passdef GenerateRandomData(self, count, gradient, offset):x1 = np.linspace(1, 5, count)x2 = gradient*x1 + np.random.randint(-10,10,*x1.shape)+offsetdataset = []y = []for i in range(*x1.shape):dataset.append([x1[i], x2[i]])real_value = gradient*x1[i]+offsetif real_value > x2[i]:y.append(-1)else:y.append(1)return x1,x2,np.mat(y),np.mat(dataset)class SimplePerceptron:def __init__(self, train_data = [], real_result = [], eta = 1):self.alpha   =   np.zeros([train_data.shape[0], 1], int)self.w   =   np.zeros([1, train_data.shape[1]], int)self.b   =   0self.eta =   etaself.train_data   = train_dataself.real_result  = real_resultself.gram         = np.matmul(train_data[0:train_data.shape[0]], train_data[0:train_data.shape[0]].T)def nomalize(self, x):if x > 0 :return 1else :return -1def train_model(self, index):temp = 0y = self.real_result.T# Here are matrix dot multiply get one valuefor i in range(len(self.alpha)):alpha      = self.alpha[i]if alpha == 0:continuegram_value = self.gram[index].T[i]temp = temp + alpha*y[i]*gram_valuey = temp + self.b# Use sign to nomalize the resultpredict_v = self.nomalize(y)return predict_v, ydef verify_model(self, x):# Here are matrix dot multiply get one valuey = np.dot(x, self.w.T) + self.b# Use sign to nomalize the resultpredict_v = self.nomalize(y)return predict_v, ydef update(self, index, x, y):# alpha = alpha + 1self.alpha[index] = self.alpha[index] + 1# b = b + n*y_iself.b = self.b + self.eta*ydef loss(slef, fx, y):return fx.astype(int)*ydef train(self, count):update_count = 0train_data_num = self.train_data.shape[0]print("train_data:", self.train_data)print("Gram:",self.gram)while count > 0:# count--count = count - 1if train_data_num <= 0:print("exception exit")break# random select one train dataindex = randint(0, train_data_num-1)if index >= train_data_num:print("exceptrion get the index")break;x = self.train_data[index]y = self.real_result.T[index]# w = \sum_{i=1}^{N}\alpha_iy_iGram[i]# wx+bpredict_v, linear_y_v = self.train_model(index)# y_i*(wx+b) > 0, the classify is correct, else it's errorif self.loss(y, linear_y_v) > 0:continueupdate_count = update_count + 1self.update(index, x, y)for i in range(len(self.alpha)):x = self.train_data[i]y = self.real_result.T[i]self.w = self.w + float(self.alpha[i])*x*float(y)print("update count: ", update_count)passdef verify(self, verify_data, verify_result):size = len(verify_data)failed_count = 0if size <= 0:passfor i in range(size-1):x = verify_data[i]y = verify_result.T[i]if self.loss(y, self.verify_model(x)[1]) > 0:continuefailed_count = failed_count + 1success_rate = (1.0 - (float(failed_count)/size))*100print("Success Rate: ", success_rate, "%")print("All input: ", size, " failed_count: ", failed_count)def predict(self, predict_data):size = len(predict_data)result = []if size <= 0:passfor i in range(size):x = verify_data[i]y = verify_result.T[i]result.append(self.model(x)[0])return resultif __name__ == "__main__":# Init some parametersgradient = 2offset   = 10point_num = 1000train_num = 1000loader = TrainDataLoader()x, y, result, train_data =  loader.GenerateRandomData(point_num, gradient, offset)x_t, y_t, test_real_result, test_data =  loader.GenerateRandomData(100, gradient, offset)# train_data = np.mat([[3,3],[4,3],[1,1]])# First trainingperceptron = SimplePerceptron(train_data, result)perceptron.train(train_num)perceptron.verify(test_data, test_real_result)print("T1: w:", perceptron.w," b:", perceptron.b)# Draw the figure# 1. draw the (x,y) pointsplt.plot(x, y, "*", color='gray')plt.plot(x_t, y_t, "+")# 2. draw y=gradient*x+offset lineplt.plot(x,x.dot(gradient)+offset, color="red")# 3. draw the line w_1*x_1 + w_2*x_2 + b = 0plt.plot(x, -(x.dot(float(perceptron.w.T[0]))+float(perceptron.b))/float(perceptron.w.T[1]), color='green')plt.show()

3、效果

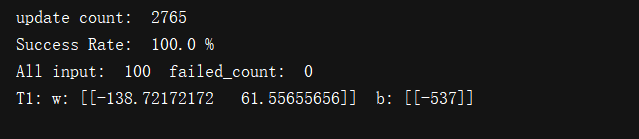
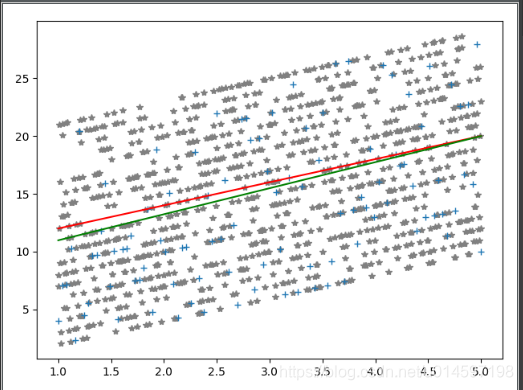
是以1000组数据训练，100组数据做验证的结果图，绿色直线为训练得到的模型。

在这次测验结果中，可以很清楚的看出，对偶形式要比原始形式得到的模型效果更好。

数学公式网站推荐

之所以推荐现成的数学公式网站，是因为CSDN在某些数学公式上支持性做的还不够完善，也希望CSDN把这里的空缺弥补上。
在线【LaTex】数学公式编辑器：http://latex.91maths.com/
本文的绝大部分公式都是在此网址上编辑的。