1080. 根到叶路径上的不足节点

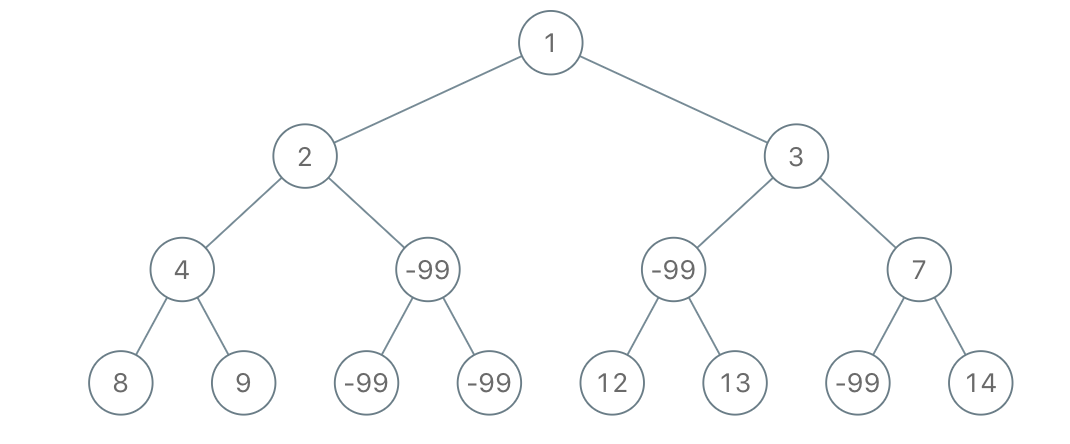
输入：root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
输出：[1,2,3,4,null,null,7,8,9,null,14]

输入：root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
输出：[5,4,8,11,null,17,4,7,null,null,null,5]

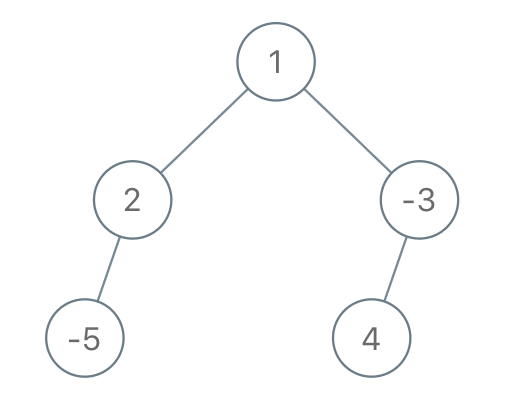
输入：root = [1,2,-3,-5,null,4,null], limit = -1
输出：[1,null,-3,4]

递归

https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/solution/python3-di-gui-xiang-jie-1080-gen-dao-xi-cc4a/

递归的过程包含两部分，一部分是向下走的“递下去”的过程，另一部分是从终点想回走的“归上来”的过程。

在你的递归函数中：

调用下一个递归函数之前，都是在为“递下去”做准备，即在“递下去”之前执行；

而在调用递归函数之后，此时操作的所有代码均为“归上来”之后执行。

以上两点是递归最重要的两部分，只有理解了这两部分，在写代码的时候才能想清楚，才能知道某些操作应该放到什么位置。

备注：递归只有在处理（递下去）的问题时，才可以转化为迭代。处理（归上来）问题时，是无法转化为迭代的。

思路

理解了上面的递归，再来看这个题目就会容易很多了。

首先我们可以开一个Map，记录每个节点对应的经过该节点的所有路径和中的最大值。

因为我们是从上面根节点出发，所以传递路径和的过程应该放在“递下去”的过程中。

而如果我们只是向下传递路径和，那么只有叶子结点才是这条路径上的路径和，而其他非叶子节点都是不完整的路径和。

所以，我们还需要在递归执行到底下，准备返回时，将叶子节点的值传上来，使得每个非叶子节点的路径和得以完整。这时候我们再去选一个左右节点传上来的路径和的最大值即可。

当然，上一段的将叶子节点的值传上来这一操作是放在归上来的位置，这显而易见。

当我们归上来到该节点时，那么就证明递归已经从下面上来了，准备继续向上走了。那此时该节点左右子树的所有值都是已经计算完成的。这时候就可以根据题意判断删除「不足节点」了。

总结一下，在一个递归函数中，顺序如下：

1. 向下传递该节点的值（前缀和思想）；
2. 执行递归函数；
3. 向上传递叶子节点的路径和，并取左右子树中路径和最大的那个；
4. 根据题意判断删除「不足节点」；

class Solution {Map<TreeNode, Integer> vals;int limit;public TreeNode sufficientSubset(TreeNode root, int limit) {this.limit = limit;TreeNode dummy = new TreeNode(0, root, null);// 记录每个节点对应的经过该节点的所有路径和中的最大值vals = new HashMap<>();dfs(dummy);return dummy.left;}public int dfs(TreeNode node){// 判断边界if(node == null) return Integer.MIN_VALUE;// 向下递归“递下去”，将自身值传递下去vals.put(node, vals.getOrDefault(node, 0) + node.val);if(node.left != null)vals.put(node.left, vals.getOrDefault(node.left, 0) + vals.get(node));if(node.right != null)vals.put(node.right, vals.getOrDefault(node.right, 0) + vals.get(node));// 只要当前节点不是叶子节点，vals[node]就是一个不完全的路径和// 需要从递归“归上来”的值中去选最大的if(node.left != null || node.right != null)vals.put(node, Math.max(dfs(node.left), dfs(node.right)));// 走到这里证明已经从下面归上来走到这里了，下面的所有值都已计算完成// 删除该删除的子节点即可if(node.left != null && vals.get(node.left) < limit)node.left = null;if(node.right != null && vals.get(node.right) < limit)node.right = null;return vals.get(node);}
}

简洁DFS

class Solution {public TreeNode sufficientSubset(TreeNode root, int limit) {limit -= root.val;if(root.left == root.right) // root是叶子// 如果 limit > 0 说明从根到叶子的路径和小于 limit，删除叶子，否则不删除return limit > 0 ? null : root;if(root.left != null) root.left = sufficientSubset(root.left, limit);if(root.right != null) root.right = sufficientSubset(root.right, limit);// 如果儿子都被删除，就删 root，否则不删 rootreturn root.left == null && root.right == null ? null : root;}
}