最小生成树

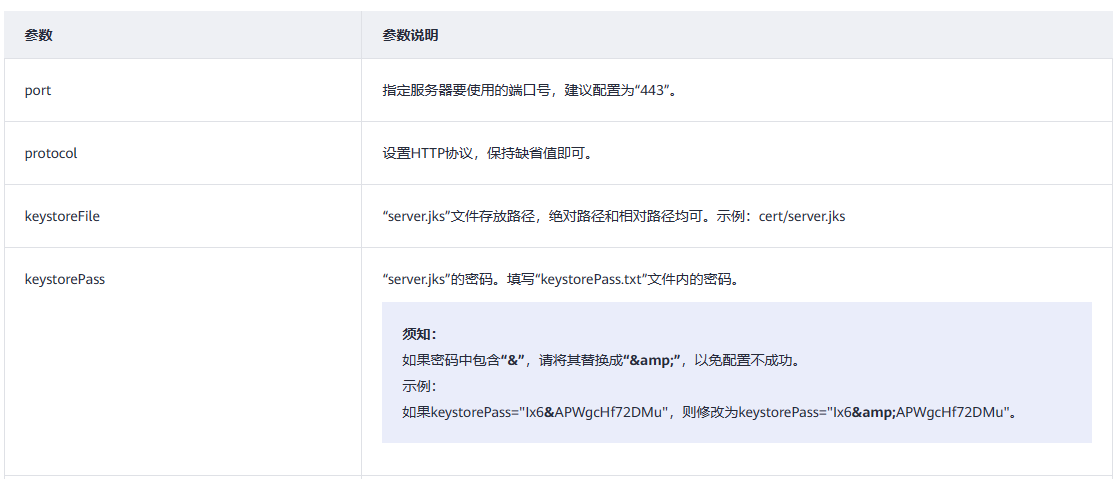
1:什么是最小生成树?

最小生成树是一个无向连通图的生成树，它的所有边的权值之和最小。也就是说，最小生成树是一棵权值最小的连通子图，其中包含了原图中的所有节点，但只保留了一部分边。最小生成树通常用于在一个图中寻找一个最小的连通子图，以便在资源有限的情况下，尽可能地覆盖原图中的所有节点。最小生成树可以用多种算法来求解，其中最常用的算法是Kruskal算法和Prim算法。

2:Kruskal算法和Prim算法

Kruskal算法：

Kruskal算法是一种基于贪心算法的最小生成树算法。它的实现方式是将所有边按照权值从小到大排序，然后依次加入生成树中，如果加入某条边后会形成环，则不加入该边。这个过程中，使用并查集来维护连通性。

Kruskal算法的时间复杂度为O(ElogE)，其中E为边的数量。Kruskal算法适用于稀疏图，即边的数量相对于节点数量较少的图。

Prim算法：

Prim算法也是一种基于贪心算法的最小生成树算法。它的实现方式是从一个节点开始，依次加入与该节点相邻的边中权值最小的边，然后再从已加入的节点中选择一个与未加入节点相邻的权值最小的边加入生成树中。这个过程中，使用优先队列来维护边的权值。

Prim算法的时间复杂度为O(ElogV)，其中E为边的数量，V为节点数量。Prim算法适用于稠密图，即边的数量相对于节点数量较多的图。

总之，Kruskal算法适用于稀疏图，Prim算法适用于稠密图。两种算法的时间复杂度都较为优秀，都可以在较短的时间内求解出最小生成树。

7-22 畅通工程之最低成本建设问题(Prim)

某地区经过对城镇交通状况的调查，得到现有城镇间快速道路的统计数据，并提出“畅通工程”的目标：使整个地区任何两个城镇间都可以实现快速交通（但不一定有直接的快速道路相连，只要互相间接通过快速路可达即可）。现得到城镇道路统计表，表中列出了有可能建设成快速路的若干条道路的成本，求畅通工程需要的最低成本。

输入格式:

输入的第一行给出城镇数目N (1<N≤1000)和候选道路数目M≤3N；随后的M行，每行给出3个正整数，分别是该条道路直接连通的两个城镇的编号（从1编号到N）以及该道路改建的预算成本。

输出格式:

输出畅通工程需要的最低成本。如果输入数据不足以保证畅通，则输出“Impossible”。

输入样例1:

输出样例1:

输入样例2:

输出样例2:

Impossible

#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
int  G[1002][1002];
int *d;  //用来记录顶点与城镇间的最小花费
bool *visit;
int inf = 0xfffffff;
int ans, n,m;void Init()
{d = new int[n + 1];visit = new bool[n + 1];fill(d, d + n + 1,inf);fill(visit, visit + n + 1, false);  fill(G[0], G[0] + 1002 * 1002, inf);int u, v, w, x;while (m--){scanf("%d%d%d", &u, &v, &w);G[u][v] = w; G[v][u] = w;}
}int mintree() //默认从第一个城镇开始，函数返回最小生成树边权之和
{d[1] = 0;  //第一个城镇到自身的最小花费为0；ans = 0;for (int i = 1; i <= n; i++){int u = -1, min = inf;for (int j = 1; j <= n; j++){if (visit[j] == false && d[j] < min){u = j;min = d[j];} //用来判断未访问点中 d[]最小的；}if (u == -1)return -1;  //如果u值为-1，则表示两地点间不连通；visit[u] = true;ans += d[u];  //进行最小边权值相加for (int v = 1; v <= n; v++){if (visit[v] == false && G[u][v] != inf && G[u][v] < d[v]){d[v] = G[u][v];}  //比较目前城市到目标城市的距离和起始点到目标城市的距离}}return ans;
}void answer(int ans)
{delete[]visit;delete[]d;if (ans == -1)printf("Impossible\n");elseprintf("%d\n", ans);
}int main()
{cin >> n >> m;Init();answer(mintree());return 0;
}

最小生成树优化(Kruskal并查集实现)

挖沟 (nowcoder.com)

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
class Node
{
public:int A, B, len;Node(int a, int b, int c){A = a;B = b;len = c;}
};
int fa[maxn], N, M, K, A, B, C, ans;
vector<Node>v;
int find(int x)
{return x == fa[x] ? x : fa[x] = find(fa[x]);
}
bool cmd(Node& A, Node& B)
{return A.len < B.len;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> N >> M;for (int i = 1; i <= N; i++)fa[i] = i;for(int i = 0; i < M; i++){cin >> A >> B >> C;v.emplace_back(A, B, C);}sort(v.begin(), v.end(),cmd);int sum = N;for (int i = 0; i < M; i++){int x = find(fa[v[i].A]);int y = find(fa[v[i].B]);if (x == y)continue;//自己指向自己不用计算并且已经入图的点也无需计算fa[x] = y;ans += v[i].len;sum--;if(1 == sum)break;}return cout << ans, 0;
}

道路建设 (nowcoder.com)Kruskal算法实现

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 110;
int N, M , K, sum, fa[maxn],A,B,len,ans;    
int find(int x){return fa[x] == x ? x : fa[x] = find(fa[x]);}
struct Node
{int A , B ,len;Node(int a,int b,int c){A = a,B = b,len = c;}
};
bool cmd(Node A,Node B)
{return A.len < B.len;
}
vector<Node>v;
signed main()
{cin >> sum >> N >> M;for(int i = 1;i <= M;i++)fa[i] = i;for(int i = 1;i <= N;i++){cin >> A >> B >> len;v.emplace_back(A,B,len);}sort(v.begin(),v.end(),cmd);int K = N;for(int i = 0;i < N;i++){int x = find(fa[v[i].A]);int y = find(fa[v[i].B]);if(x == y)continue;fa[x] = y;ans += v[i].len;K--;if(K == 1)break;}ans <= sum ? cout << "Yes" : cout << "No" ;return 0;
}

Forsaken喜欢独一无二的树 (nowcoder.com)

重构最小生成树(Kruskal)

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 2e5 + 10;
int N, M, K, sum, fa[maxn], A, B, len, ans;
struct Node {int A, B, len; Node(int a, int b, int c) { A = a, B = b; len = c; }
};int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }bool cmd(Node A, Node B) { return A.len < B.len; }vector<Node>v;void Kruskal(){sort(v.begin(), v.end(), cmd);for (int i = 0; i < M; ){//对于M条选择进行枚举int j;for (j = i; v[i].len == v[j].len; j++){//最小生成树每一步都取最优解,如果出现多种最小生成树的情况,那么一定是有N条边权是相同的,将其全部记录下来if (find(v[j].A) != find(v[j].B))//前提条件:A B点为被纳入最小生成树中ans += v[j].len;}for (; i < j; i++){int fx = find(v[i].A), fy = find(v[i].B);if (fx != fy) fa[fx] = fy, ans -= v[i].len;//保留一条最优的生成树路径}}cout << ans;}signed main(){cin >> N >> M;for (int i = 1; i <= N; i++)fa[i] = i;for (int i = 1; i <= M; i++){cin >> A >> B >> len;v.emplace_back(A, B, len);}Kruskal();return 0;}

[SCOI2012]滑雪与时间胶囊 (nowcoder.com)

#include<bits/stdc++.h>
using namespace std;
const long long inf = 1e18;
const int N = 1e6 + 5;
const double eps = 1e-10;
const int mod = 1e9 + 7;
typedef long long ll;
struct Edge {int v, nextz;ll cost;
}edge[N << 1];
int tot, head[N];
void addedge(int u, int v, ll w) {edge[tot].v = v;edge[tot].cost = w;edge[tot].nextz = head[u];head[u] = tot++;
}
struct qnode {int v, h;ll dis;qnode(int _v = 0,int  _h = 0, ll _dis = 0): v(_v), h(_h), dis(_dis){}bool operator < (const qnode &s) const {return h == s.h ? dis > s.dis : h < s.h;}
};int val[N], cnt, n, m;;
bool vis[N];
ll dist[N], ans;
void prim() {for(int i = 1; i <= n; i++) dist[i] = inf;priority_queue<qnode> q;q.push(qnode(1, val[1], 0));dist[1] = 0;while(!q.empty()) {qnode tmp = q.top();q.pop();int u = tmp.v;if(vis[u]) continue;vis[u] = 1;cnt++, ans += dist[u];for(int i = head[u]; ~i; i = edge[i].nextz) {int v = edge[i].v;ll cost = edge[i].cost;if(!vis[v] && dist[v] > cost) {dist[v] = cost;q.push(qnode(v, val[v], dist[v]));}}}
}
int main() {cin.tie(0)->sync_with_stdio(false);memset(head, -1, sizeof(head));cin >> n >> m;            for(int i = 1; i <= n; i++) cin >> val[i];while(m--) {int u, v;ll w;cin >> u >> v >> w;if(val[u] >= val[v]) addedge(u, v, w);if(val[v] >= val[u]) addedge(v, u, w);}prim();cout << cnt << ' ' << ans << "\n";return 0;
}