平均值概述
平均数反映了一组数据的一般水平,最常见的平均数是算术平均数,除了算数平均数外,还有几何平均数,调和平均数,加权平均数等。
算术平均值(Arithmetic Mean)
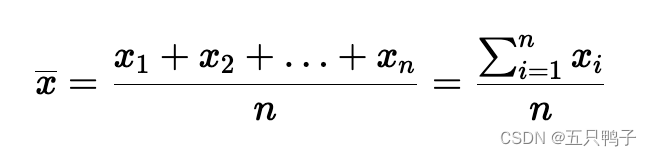
-
公式解读:表示为所有项之和再除以总数。
-
应用场景:算术平均值是我们生活中最常见的平均值,比较适用于符合正态分布的一组数,比如班级的平均年龄,平均分等。不太适用于有极端值的一组数,例如平均收入。
加权平均值(Weighted Mean)

- 公式解读:表示为每项 Xi 乘以它的权重 Wi 之和 除以所有的权重之和
- 应用场景:适用于计算一组权重不同的数中的平均值,例如学生的GPA,每门课的学分(权重)都不一样。
几何平均值(Geometric Mean)
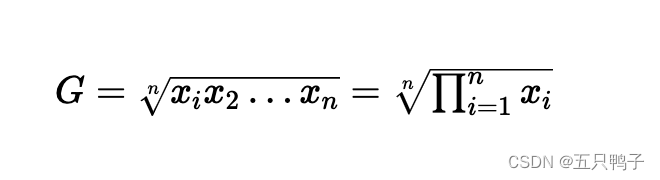
- 注意点:几何平均值只针对于正数,也就是说Xn 都必须是正数
- 公式解读:每项的连乘积开项数次方根
- 应用场景:几何平均值多用于计算速率,例如平均增长率,平均利率等
调和平均值(Harmonic Mean)
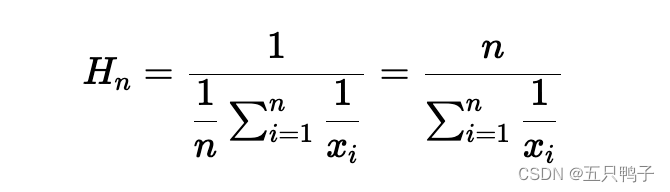
- 注意点:
- 容易受极端值的影响,受极小值的影响比极大值的影响要大。
- 所有项中的值都不能为0,只要有一个为0,分母就为0了,就没有意义了。
- 公式解读:调和平均数又称为倒数平均值,是总体各统计变量倒数的算术平均数的倒数
- 应用场景:调和平均数应用场景较少,通常应用在分段求平均数的场景中,比如阶梯电价等。
各个平均数大小对比
算数平均值 ≥ 几何平均值 ≥ 调和平均值