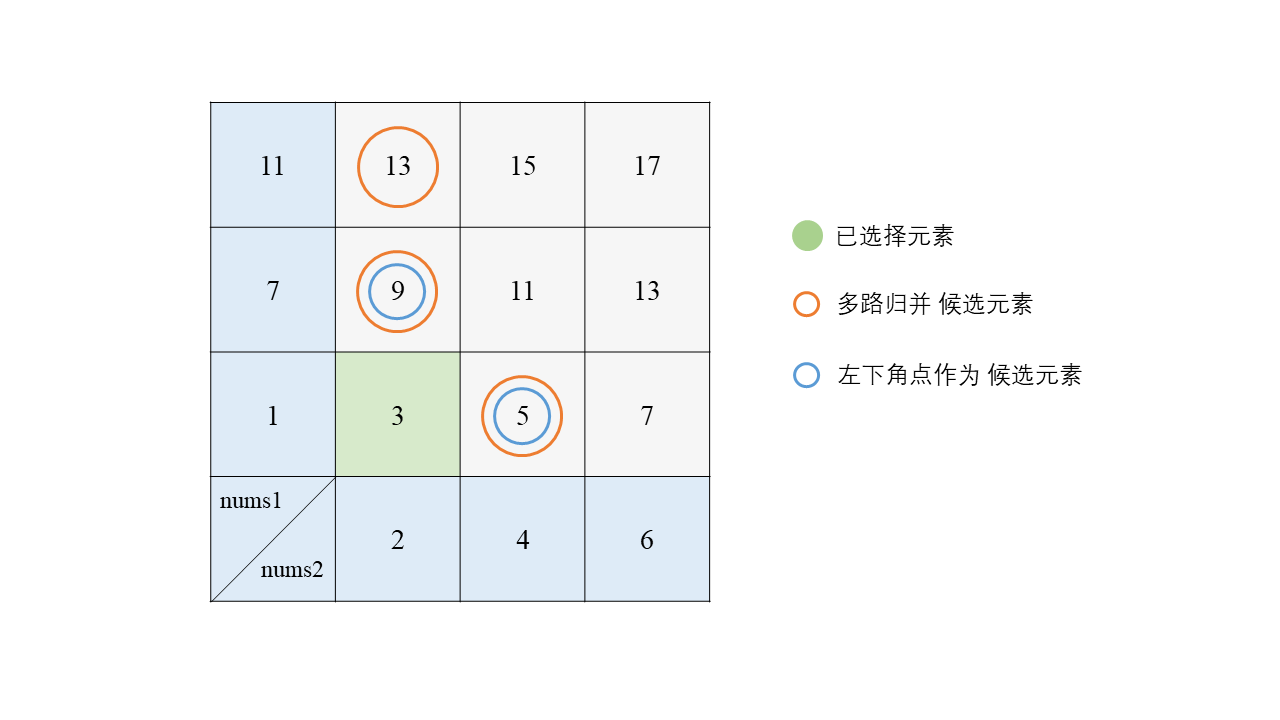
查找和最小的k对数

思路：
该题一开始想用双指针来做，哪个指针与下一个数之前的gap越小，则移动哪个指针。这对k比较小的情况能够求解，但是k比较大时，需要回退至之前的元素，而双指针却做不到，得用一个数据结构来存储之前的状态。于是我们想到用堆来求解。
解法：堆

1. 构建小顶堆，初始元素为nums1[0]+nums2[0]。
2. 弹出堆顶元素nums1[i]+nums2[j]（当前最小元素），若存在下一元素(j+1<len(nums2)，则添加nums1[i]+nums2[j+1]，若不存在，则继续弹出，
3. 若j==0，则表明当前i状态下最小元素和已弹出，则进入下一状态，nums1[i+1]+nums2[0]入堆，这时可能仍然有nums1[i]+nums2[j]，j!=0在堆中，后续可能弹出（解决之前双指针面临的回退问题）。
4. 后续重复步骤2、3，直至堆为空或结果列表等于k。
   总结：
   解决此类topK的问题，一般都可以尝试用堆来解决。

class Solution:def kSmallestPairs(self, nums1, nums2, k):h = []from heapq import heappop,heappushdef push(i, j):if i < len(nums1) and j < len(nums2):heappush(h, [nums1[i] + nums2[j], i, j])push(0, 0)pairs = []while h and len(pairs) < k:_, i, j = heappop(h)pairs.append([nums1[i], nums2[j]])push(i, j + 1)if j == 0:push(i + 1, 0)return pairs

棒球比赛

解法：模拟
这题比较简单，按照题意构造一个栈，因为我们只处理涉及栈顶或倒数第二个元素的操作。

class Solution:def calPoints(self, ops: List[str]) -> int:score = 0result = []for op in ops:if op == "C":score -= result[-1]result.pop()elif op == "D":score += result[-1]* 2result.append(result[-1]* 2)elif op == "+":score += result[-1] + result[-2]result.append(result[-1] + result[-2])else:score += int(op)result.append(int(op))return score