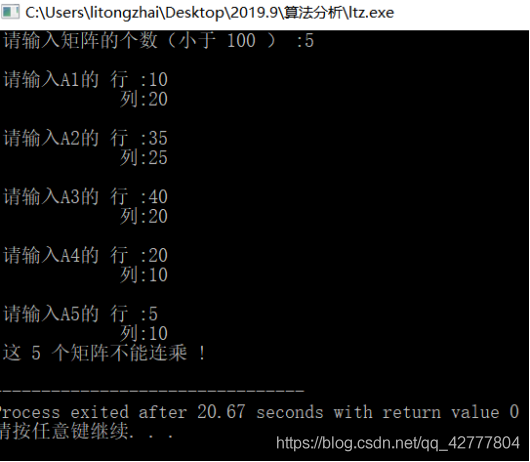
n个矩阵连乘的问题

给定n个矩阵{A1，A2，……，An},其中Ai与Ai+1是可乘的，i=1，2，……，n-1。

例如：

计算三个矩阵连乘{A1，A2，A3}；维数分别为10100 , 1005 , 5*50

按此顺序计算需要的次数((A1*A2)*A3):10X100X5+10X5X50=7500次

按此顺序计算需要的次数(A1*(A2*A3)):10X5X50+10X100X50=75000次

所以要解决的问题是：如何确定矩阵连乘积A1A2，……An的计算次序，使得按此计算次序计算矩阵连乘积需要的数乘次数达到最小化。

问题分析与描述：

两个矩阵r1r2和r2r3的矩阵相乘需r1r2r3次乘法，那么n个矩阵相乘就得到很多种不同的计算方法其中乘法最少的所花费的时间肯定最少。

那什么方法才能最快呢？

我们先了解加括号：
我们在每一个矩阵外面加一个括号，这样结果是不变的。但是当在两个矩阵外加一个括号运算方法被改变了((A1A2)A3)这两个(A1(A2A3))就是这样
然后最广到n的情况怎么不同的括号结果也就不一样了最后我们求取最快的结果即可

现在我们把这个矩阵这道题改变成加括号如何加括号才能使得最后的结果是最快的

算法设计与思路

我们将这个相乘的问题改变为加括号后我们来分析：
以6个矩阵为例：
在这里插入图片描述

这是四个矩阵和他们的维数我们先自顶向上想求取最后结果：
M1-4可以（A1）M1-3 or （A1A2）（A3A4）或者M1-3*A4
这三种情况然后M值按以下的这颗树这样向下分
我们将这个画成一棵树即为
在这里插入图片描述
最终我们在二叉树左右节点的位置求出最后小值就可得到最后答案M1-4

这里我们可以发现是需要计算很多重复值如何减少这些浪费的时间呢？

我们可以创建一个二维数组记录每一个保存的数据
用i表示行j表示列的话 Mi-j表示i到j中最小的计算次数。
当i=j时为0我们可以创建以下的二维数组m
在这里插入图片描述

最终的答案即为m[1][4]
我们在表示每次插入的括号如
在这里插入图片描述

再次建立一个二维数组com起始为0
则我们看到com【0】【2】=1我们就认为在第一个元素后加入括号A1M23
com【0】【3】=3我们在第三个矩阵后加入括号M13A44；

伪代码：

course（int i，j）
{int u,k,t;
if(m[i][j]>=0
return m[i][j];
if(i==j) return 0;
if(i=j-1){
com[i][j+1]=i;
m[i][j]=r[i]*r[i+1]*r[i+2];
return m[i][j];}
u=course(i,i)+course(i+1,j)+r[i*r[k+1*r[j+1];
com[i][j]=i;
for(k=i+1 ;k<j;k=k+1){
t=course(i,i)+course(i+1,j)+r[i*r[k+1*r[j+1];
if(t<u){
u=t;
com[i][j]=k;
}
}
m[i][j]=u;
return u;
}

c程序

#include<stdio.h>
int m[6][6];
int com[6][6];
int r[7]={30,35,15,5,10,20,25};
int course(int i,int j){printf("i=%dj=%d\n",i,j);int u,s;if(m[i][j]>=0){return m[i][j];}if(i==j){m[i][j]=0;return 0;}if(i==j-1){m[i][j]=r[i]*r[i+1]*r[i+2];com[i][j]=i+1;return r[i]*r[i+1]*r[i+2];}printf("i=%d\n",i);u=course(i,i)+course(i+1,j)+r[i]*r[i+1]*r[j+1];com[i][j]=i+1;for(int k=i+1;k<j;k++){s=course(i,k)+course(k+1,j)+r[i]*r[k+1]*r[j+1];printf("i=%dj=%dk=%d\t%d\n",i,j,k,s);if(u>s){u=s;com[i][j]=k+1;}}m[i][j]=u;return u;
}
int main(){int n=6;for(int i=0;i<6;i++){for(int j=0;j<6;j++){m[i][j]=-1;com[i][j]=0;}}printf("最后答案%d\n",course(0,n-1));for(int i=0;i<6;i++){printf("\n");for(int j=0;j<6;j++){printf("m[%d][%d]%d\t",i,j,m[i][j]);}}for(int i=0;i<6;i++){printf("\n");for(int j=0;j<6;j++){printf("com[%d][%d]%d\t",i,j,com[i][j]);}}
}