目录
1 主要内容
广义benders分解法流程图:
优化目标:
约束条件:
2 部分代码
3 程序结果
4 下载链接
1 主要内容
该程序复现文章《综合能源系统协同运行策略与规划研究》第四章内容基于广义Benders分解法的综合能源系统优化规划,代码主要构建了以最小化包括初始投资和运行成本的总成本为优化目标的综合能源系统优化规划模型。模型上层是综合能源系统中相关设备的初始投资成本,下层以第三章所提出的综合能源优化运行问题为子问题,综合考虑风机、光伏随机性以及普遍存在的负荷预测误差等因素,通过广义Benders分解法进行求解。最后通过实际案例仿真分析,验证本文所提优化规划方法论可以实现综合能源系统在规划期内经济性最优,有力支撑了实际综合能源系统建设规划的策略依据。

广义benders分解法流程图:

优化目标:


约束条件:

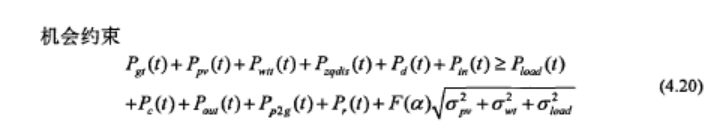
2 部分代码
%% 气网 m=14;n=16; % 节点与支路个数 isb=1; pr=0.0001; BH=1.2;%压缩机常数 ZH=1.2;%压缩机常数 B1=[1 2 0.2526 1 % 4列分别为首节点i、末节点j、Kij和支路编号1 3 0.2410 22 3 0.2990 32 4 0.2924 43 6 0.2777 54 5 0.2777 6 % *5 8 0.2365 76 7 0.1662 8 % *7 10 0.1662 98 9 0.2365 10 % *9 12 0.1634 1110 11 0.1493 12 % *11 13 0.1493 1312 13 0.1598 1412 14 0.1665 1513 14 0.1534 16]; % 支路矩阵 B2=[1 0 1 0 1200; % 5列分别为节点编号、节点类型、压缩机比例、节点负荷和节点压力2 1 1 20 7003 1 1 20 6804 1 1 40 5205 1 1 60 8706 1 1 0 5007 1 1 20 9008 1 1 30 7209 1 1 0 100010 0 1 0 70011 1 1 0 110012 1 1 40 68013 1 1 20 72014 1 1 80 650]; % 节点矩阵 类型为1的节点压力为自定义初值 类型为0的节点压力保持 B2(:,4)=abs(B2(:,4)); B1(:,3)=4.*B1(:,3); %不收敛情况 %B2(:,5)=[1109.67741935484,993.548387096774,1022.58064516129,790.322580645161,587.096774193548,1022.58064516129,906.451612903226,616.129032258065,761.290322580645,848.387096774194,935.483870967742,1022.58064516129,1022.58064516129,1080.64516129032]; A0 = zeros(m,n); % 构建关联矩阵A0 (m x n) for i=1:16for j=1:14if B1(i,1)==jA0(j,i) = -1;endif B1(i,2)==jA0(j,i) = 1;end end end % for i = 1:m % for j=1:n % COUNT1=[]; % if B1(j,1)==i % COUNT1=[COUNT1 B1(j,4)]; % end % A0(i,COUNT1) = 1; % end % for j=1:n % COUNT2=[]; % if B1(j,2)==i % COUNT2=[COUNT2 B1(j,4)]; % end % A0(i,COUNT2) = -1; % end % end A0; % 显示A0 A1 = A0(2:m,:); % 构建缩减关联矩阵A1 A1; % 显示A1 for i=1:n % 计算流量if B2(B1(i,1),5)^2 > B2(B1(i,2),5)^2S(i)=1;elseS(i)=-1;endDetaP(i) = B2(B1(i,1),5)^2 - B2(B1(i,2),5)^2;f(i) = B1(i,3)*S(i)*sqrt(S(i)*DetaP(i)); end P = B2(2:m,5); for i=1:m-1PAI(i)=P(i)^2; end PAI = PAI'; % 显示PAI f = f'; % 把流量f转化为列向量 L = B2(2:m,4); % 负荷列向量L F = A1*f-L; kk=1;
3 程序结果
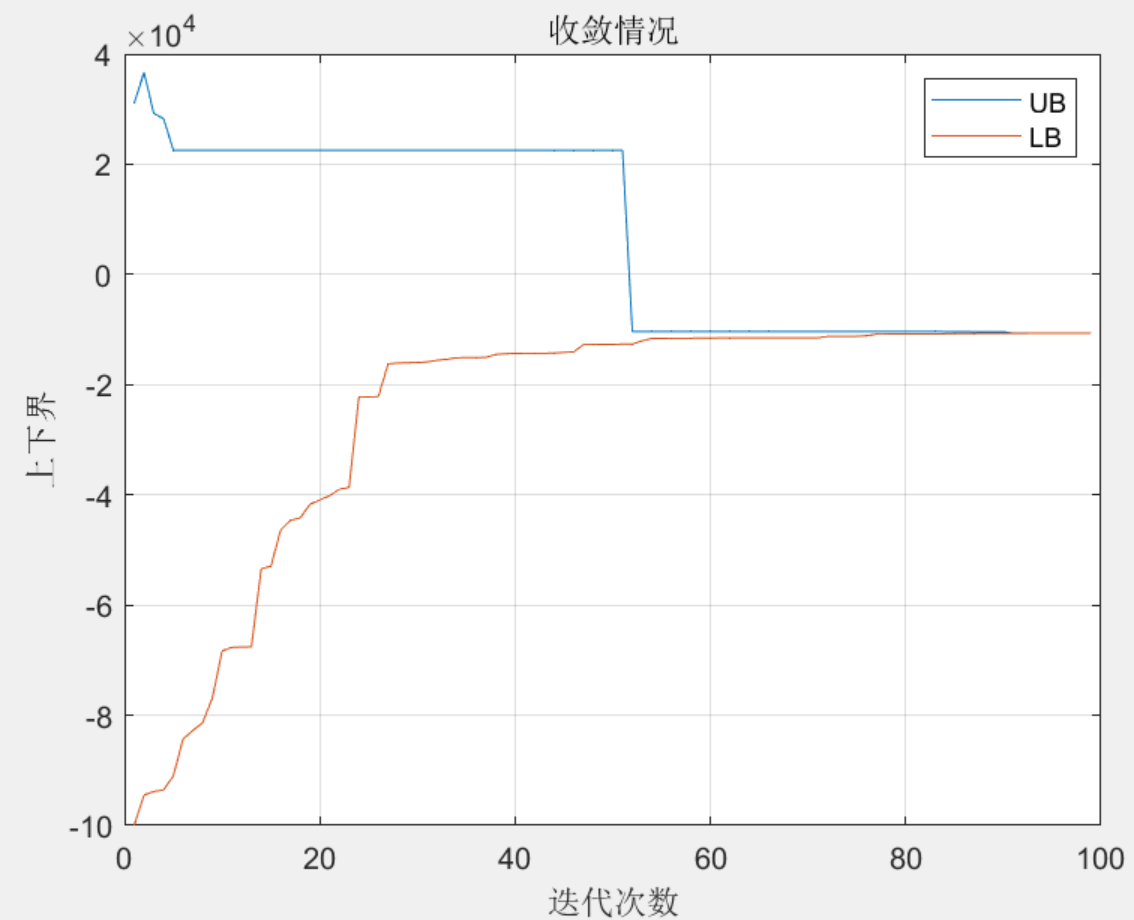
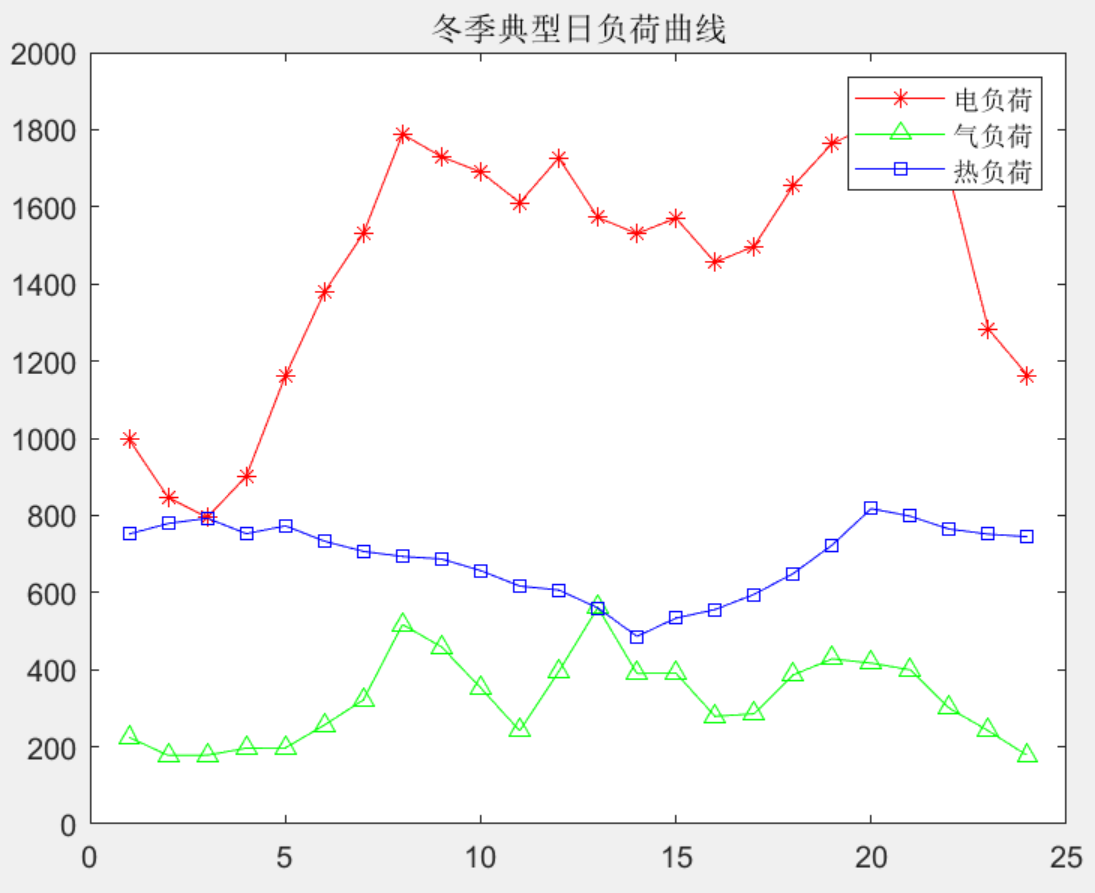
原文结果图:
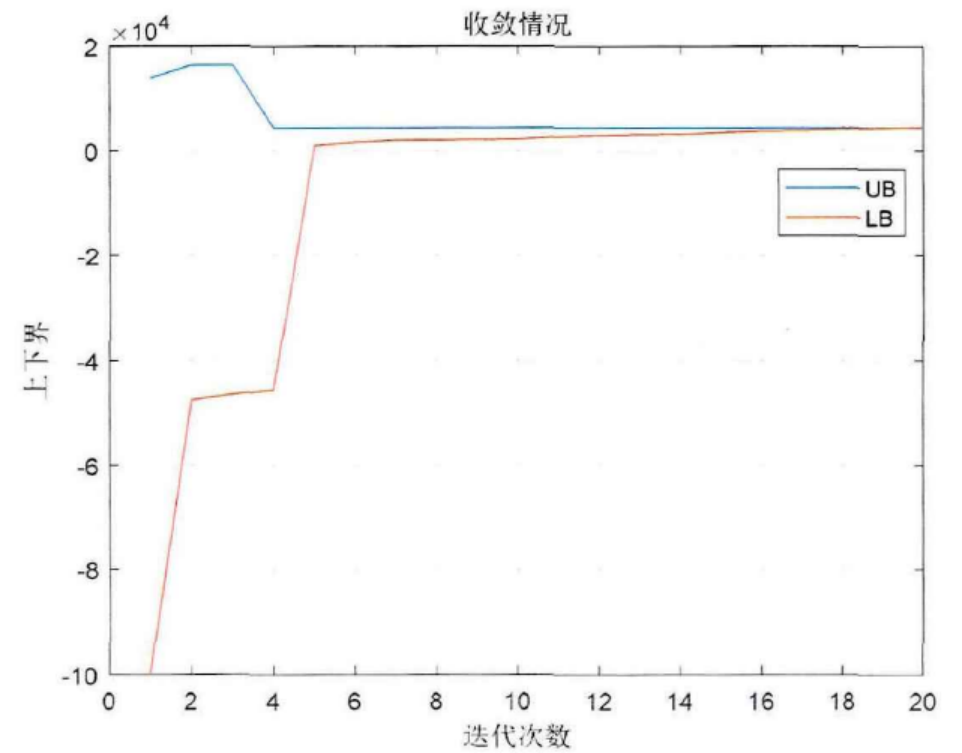
从结果对比看,本程序收敛性能达到预期!
4 下载链接
点击直达!