下图转自“英式没品笑话百科”的新浪微博 —— 所以无论有没有遇到难题,其实都不用担心。
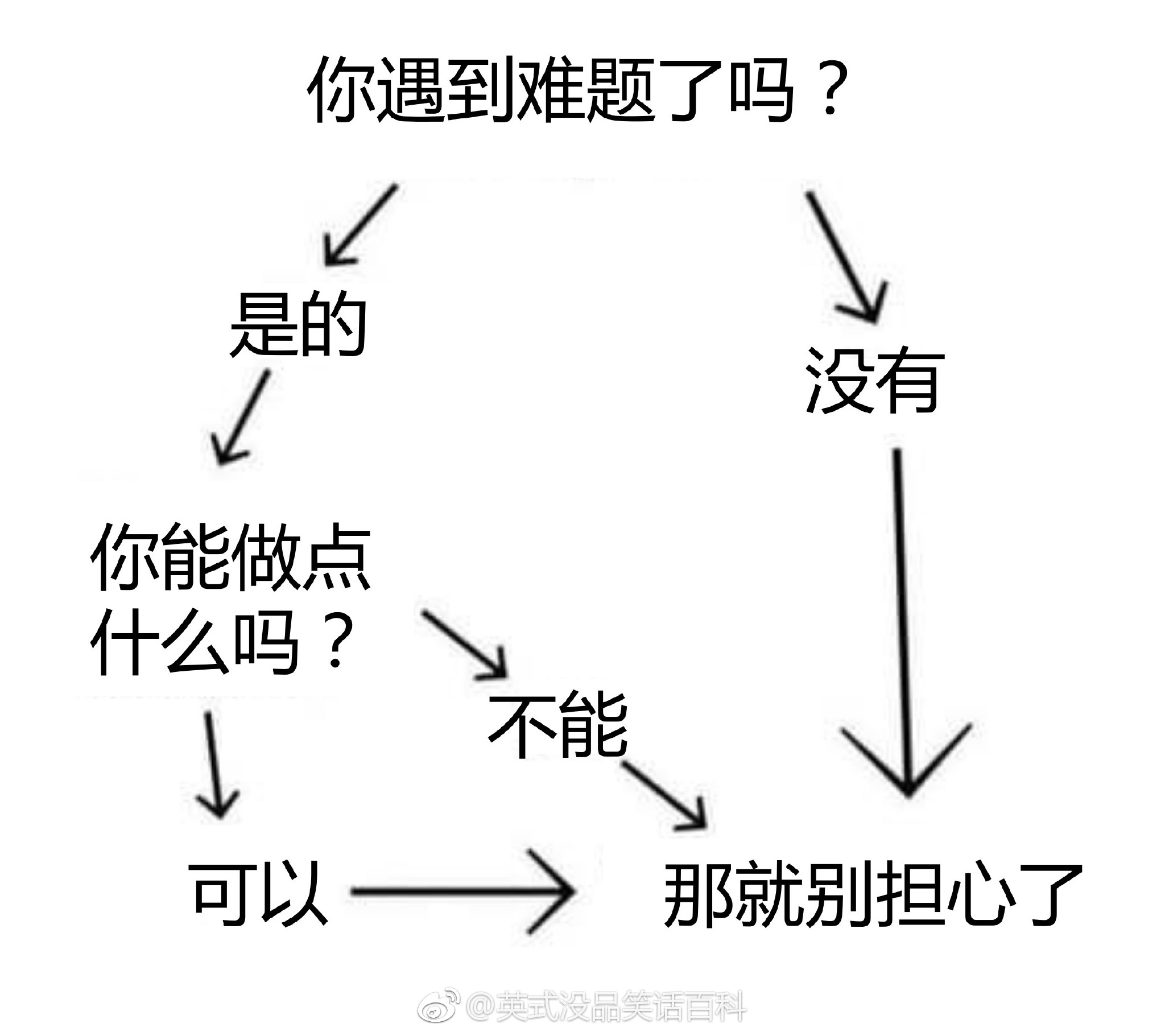
博主将这种逻辑推演称为“逻辑自洽”,即从某个命题出发的所有推理路径都会将结论引导到同一个最终命题(开玩笑的,千万别以为这是真正的逻辑自洽的定义……)。现给定一个更为复杂的逻辑推理图,本题就请你检查从一个给定命题到另一个命题的推理是否是“逻辑自洽”的,以及存在多少种不同的推理路径。例如上图,从“你遇到难题了吗?”到“那就别担心了”就是一种“逻辑自洽”的推理,一共有 3 条不同的推理路径。
输入格式:
输入首先在一行中给出两个正整数 N(1<N≤500)和 M,分别为命题个数和推理个数。这里我们假设命题从 1 到 N 编号。
接下来 M 行,每行给出一对命题之间的推理关系,即两个命题的编号 S1 S2,表示可以从 S1 推出 S2。题目保证任意两命题之间只存在最多一种推理关系,且任一命题不能循环自证(即从该命题出发推出该命题自己)。
最后一行给出待检验的两个命题的编号 A B。
输出格式:
在一行中首先输出从 A 到 B 有多少种不同的推理路径,然后输出 Yes 如果推理是“逻辑自洽”的,或 No 如果不是。
题目保证输出数据不超过 109。
输入样例 1:
7 8
7 6
7 4
6 5
4 1
5 2
5 3
2 1
3 1
7 1
输出样例 1:
3 Yes
输入样例 2:
7 8
7 6
7 4
6 5
4 1
5 2
5 3
6 1
3 1
7 1
输出样例 2:
3 No
代码长度限制
16 KB
时间限制
400 ms
内存限制
DFS
30行代码(运行超时23分)最后一个过不了
#include<bits/stdc++.h>
using namespace std;
const int maxn = 500 + 10;
int N, M, K, A, B, D, NUM;
vector<vector<int>>v(maxn);
bool ok = true;
int DFS(int start, int enl)
{if (start == enl) return NUM++;for (auto i : v[start]){if(v[i].size() == 0 && i != enl)ok = false;DFS(i, enl); }
}int main()
{cin >> N >> M;//N个命题M个推理while (M--){cin >> A >> B;v[A].emplace_back(B);}cin >> K >> D;DFS(K, D);if(!NUM)ok = false;ok ? cout << NUM << ' ' << "Yes" : cout << NUM << ' ' << "No";return 0;
}画一个图分析一下
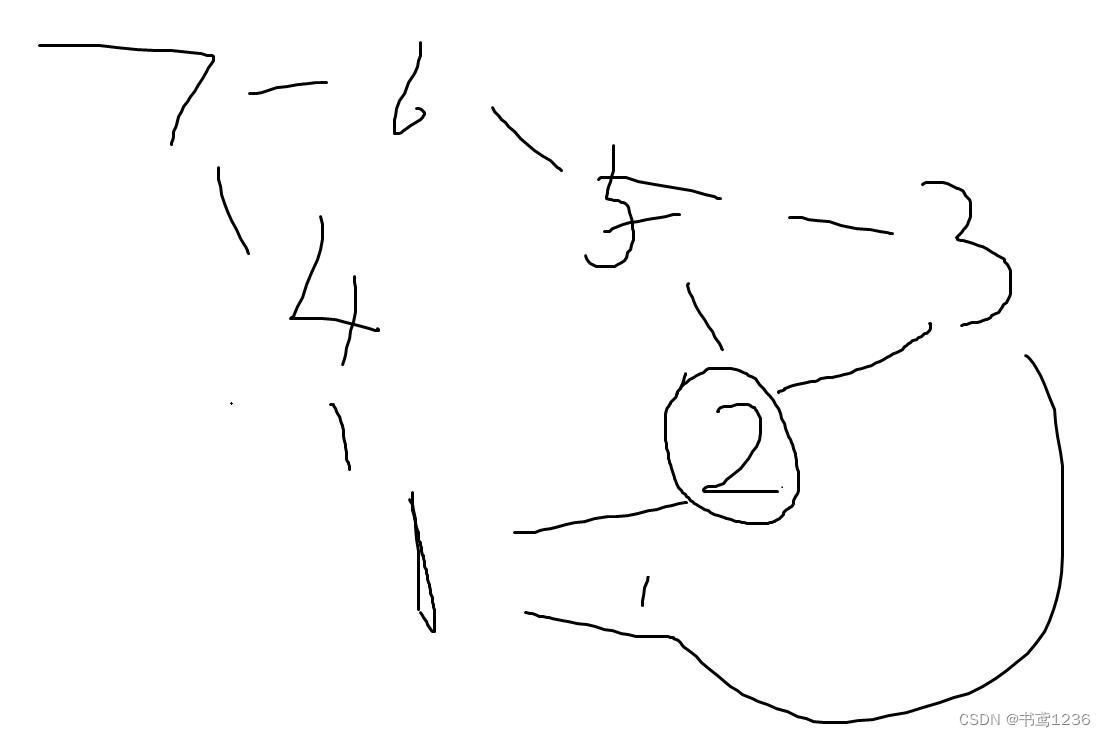
如果多连几条线例如:6->5 6->2 ………… 以及当N == 500时,每一条线都连接499个点,直接暴搜会出现一个点重复被访问了多次的情况确实浪费时间,优化也从这方面下手
根据样例:反过来看到1的点无非2 3 4那么可以认为2和3,4到1的路径有1条
5可以到2 3,对于5而言因为我们已知2和3只有1条路径可以到1,所以5到1的路径就应该是Road[2]+Road[3] = 2,递推得Road[7] = Road[4] + Road[6] = Road[4] + Road[5] = 3
因此我们不妨引入一个数组Road记录各点出发到达终点有多少条路径,当我们重复访问到已被记录的点时就省去了再跑一遍的时间,直接反馈答案。
AC代码如下(18ms)
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
const int maxn = 500 + 10;
int N, M, K, A, B, D, NUM, Road[maxn];
vector<vector<int>>v(maxn);
bool ok = true;
int DFS(int start, int enl)
{if (start == enl)return 1;if (Road[start])return Road[start];for (auto i : v[start]){if (v[i].size() == 0 && i != enl)ok = false;Road[start] += DFS(i, enl);}return Road[start];
}int main()
{IOS cin >> N >> M;//N个命题M个推理while (M--){cin >> A >> B;v[A].emplace_back(B);}cin >> K >> D;DFS(K, D);if (!Road[K])ok = false;ok ? cout << Road[K] << ' ' << "Yes" : cout << Road[K] << ' ' << "No";return 0;
}

