滤波总结+应用举例1(kalman滤波、序贯滤波、UD分解滤波、遗忘滤波、信息滤波、自适应滤波)（内含matlab代码）

news/2024/11/8 2:50:17/

最近在研究滤波的相关知识，在此写个总结，以免自己遗忘。
卡尔曼滤波其实是一种估计方法，在已知前一时刻的状态量和当前时刻的量测情况下，估计当前状态量。
1、首先介绍常规kalman filter（含详细代码及标注）
举一个例子便于更详细地说明：
假设有一巡航导弹飞向目标，在目标处设有监视雷达，雷达对导弹距离进行量测。已知：导弹距目标初始距离为100km，速度约为280m/s，基本匀速飞行，但受空气扰动，扰动加速度为零均值白噪声，方差强度为q=0.1m2/s3,；雷达观测频率为2Hz，观测误差为零均值白噪声，均方差为50m。
这一问题的离散状态空间模型可写成：
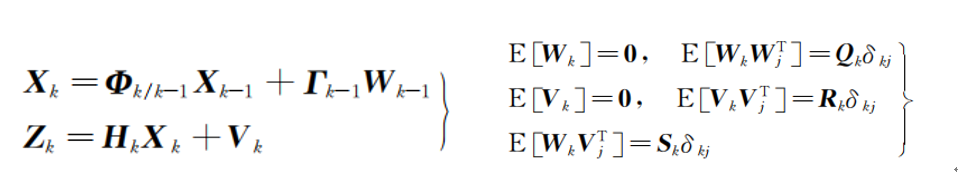
在这里插入图片描述

该式子表明，过程噪声和量测噪声都是零均值的白噪声且相互无关。
在这里插入图片描述
状态方程：
此处，设状态标量x1导弹距目标距离，x2导弹速度，易知：
x1(k)=x1(k-1)-x2(k-1)×Ts; x2(k)=x2(k-1)+w2扰动
Ts=1/f=1/2=0.5s，Qk=q×Ts=0.05m2/s2;
由此可以得出，phi=[1,-0.5;0,1]; gamma=[0;1]
量测方程：
量测方程通常都是以离散的形式给出的，不需要进行离散化。
量测变量只有一个，z表示雷达观测到的导弹距目标距离。
z(k)=x1(k)+v(k)；v(k)是肯定存在的，表示雷达观测的误差，如果不存在就不需要经过估计了。
H=[1;0];Rk=50^2 (注意这里单位要化一致)

看代码：

clear;clc;clear all;
%% 初始化参数
T =2000;                   % 仿真时长
qt = 0.1;                   % 过程噪声 ，单位m^2/s^3
Rk = 50^2;                    % 量测噪声,单位m^2
T_mea = 0.5;               % 量测采样时间
Qk = qt*T_mea;                %单位m^2/s^2
W = sqrt(Qk)*randn(1,T);
V = sqrt(Rk)*randn(1,T); 
% 系统矩阵
Phi = [1 -0.5;0 1];            % 状态矩阵
I = eye(2);
H = [1,0];                 % 量测矩阵
Gamma = [0;1];
% 初始化
nS = 2; nZ = 1;
count = 1;                 % 用于计数
xState = zeros(nS,T);
zMea = zeros(nZ,T);
xState(:,1) = [100000;280];xState1(:,1) = [100000;280];
zMea(:,1) = H*xState(:,1);
%% 02 用模型模拟真实状态
for t = 2:TxState(:,t) = Phi*xState(:,t-1) + Gamma*W(:,t);zMea(:,t) = H*xState(:,t) + V(t);
endxKF = zeros(nS,T);xKF1 = zeros(nS,T);
xKF_pre = zeros(nS,T);xKF_pre1 = zeros(nS,T);
xKF(:,1) = xState(:,1); xKF1(:,1) = xState(:,1);
P0 = diag([1,1])^2; P1 = diag([1,1])^2;
%% 03 卡尔曼滤波
for t = 2:T% 状态一步预测xKF_pre(:,t) = Phi*xKF(:,t-1);          %预测距离% 状态一步预测均方误差P_pre = Phi*P0*Phi' + Gamma*Qk*Gamma';   %预测距离均方误差% 滤波增益K = P_pre*H'*pinv(H*P_pre*H'+Rk);        % 状态估计xKF(:,t) = xKF_pre(:,t) + K*(zMea(:,t)-H*xKF_pre(:,t));%距离估计% 状态估计均方误差P0 = (I-K*H)*P_pre;%距离估计均方误差
end

2、序贯滤波
上面求滤波增益过程中存在矩阵求逆过程，当量测维数较大时，计算过于复杂，序贯滤波是一种将高维数量测更新降低为多个低维数量测更新的方法。
在这里插入图片描述
序贯滤波相较于常规kalman的不同之处在于量测更新，它将量测更新分解为N个子量测更新，k时刻的所有子量测更新等效于是在初值x p条件下进行的N次递推最小二乘估计，最后结果最为输出。
在这里插入图片描述
在这里插入图片描述
看代码：

clc;clear;clear all;
d0=100000;
v0=280;
q0=0.1;
f0=5;
r01=50;
r02=1;
%数据处理
length1=ceil(f0*d0/v0)+f0*50;%估计数据的数量
t=zeros(1,length1);%时间
s=zeros(1,length1);%导弹运动的距离
dl=zeros(1,length1);dl(1)=d0;%雷达观测距离
v=zeros(1,length1);v(1)=v0;%导弹速度
Ts=1/f0;%采样时间间隔
for i=1:length1t(i)=(i-1)*Ts;
end
for j=2:length1s(j)=s(j-1)+v(j-1)*Ts;v(j)=v(j-1)+sqrt(q0*Ts)*randn(1);dl(j)=d0-s(j)+sqrt(r01^2)*randn(1);%量测距离if d0-s(j)<0breakend
end
t=t(1,1:j);s=s(1,1:j);dl=dl(1,1:j);v=v(1,1:j);%更新数据
vl=v+sqrt(r02^2)*randn(1);%雷达观测速度
%序贯滤波
Xx2=zeros(2,j);Px21=zeros(j,1);Px22=zeros(j,1);%存储滤波得到的数据
Xx2(:,1)=[0 280]';Px21(1)=2500;Px22(1)=100;%初值
phix=[1 0.2;0 1];gammax=[0 1]';Qx=q0*Ts;  Rx=diag([r01^2 r02^2]);Hx=[1 0;0 1];
for m=2:jXx1=Xx2(:,m-1);Px1=[Px21(m-1) 0;0 Px22(m-1)];Zkx=[100000-dl(m-1);vl(m-1)];[Xx,Px]=xuguan(phix,gammax,Qx,Rx,Hx,Xx1,Px1,Zkx);Xx2(1,m)=Xx(1);Xx2(2,m)=Xx(2);Px21(m)=Px(1,1);Px22(m)=Px(2,2);
end
function [ Xk, Pk ] = xuguan( phi,gamma,Q,R0,H0, X1,P1,Zk0)
l=length(X1);   
n=length(Zk0);
Xk1=phi*X1;%状态一步预测
Pk1=phi*P1*phi'+gamma*Q*gamma';%状态一步预测均方误差
for k=1:nR=R0(k,k);Zk=Zk0(k);H=H0(k,:);Kk=Pk1*H'*((H*Pk1*H'+R)^-1);%滤波增益Xk=Xk1+Kk*(Zk-H*Xk1);%状态估计Pk=(eye(l)-Kk*H)*Pk1;%状态估计均方误差Xk1=Xk;Pk1=Pk;
end
end

3、UD分解滤波
UD分解滤波是平方根滤波的一种，即在求解过程中将P表示成UD分解形式，可以提高计算精度，不过现在已经不怎么用这种方法了。
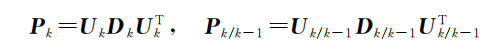
在这里插入图片描述
基本思路如下：
在这里插入图片描述
看代码：

clear;clc;clear all;
%% 初始化参数
T =2000;                   % 仿真时长
qt = 0.1;                   % 过程噪声 ，单位m^2/s^3
Rk = 50^2;                    % 量测噪声,单位m^2
T_mea = 0.5;               % 量测采样时间
Qk = qt*T_mea;                %单位m^2/s^2
W = sqrt(Qk)*randn(1,T);
V = sqrt(Rk)*randn(1,T); 
% 系统矩阵
Phi = [1 -0.5;0 1];            % 状态矩阵
I = eye(2);
H = [1,0];                 % 量测矩阵
Gamma = [0;1];
% 初始化
nS = 2; nZ = 1;
count = 1;                 % 用于计数
xState = zeros(nS,T);
zMea = zeros(nZ,T);
xState(:,1) = [100000;280];xState1(:,1) = [100000;280];
zMea(:,1) = H*xState(:,1);
%% 02 用模型模拟真实状态
for t = 2:TxState(:,t) = Phi*xState(:,t-1) + Gamma*W(:,t);zMea(:,t) = H*xState(:,t) + V(t);
end
xKF = zeros(nS,T);xKF1 = zeros(nS,T);
xKF_pre = zeros(nS,T);xKF_pre1 = zeros(nS,T);
xKF(:,1) = xState(:,1); xKF1(:,1) = xState(:,1);
P0 = diag([1,1])^2; P1 = diag([1,1])^2;
%% 03 UD分解滤波
Q=Qk;R=Rk;
[U,D]=myudut(P1);%%对初值P1进行分解
U1=U;U2=U;D1=D;D2=D;
for t = 2:TxKF_pre1(:,t) = Phi*xKF1(:,t-1);[U1,D1]=UDKF(U1,D1,Phi,Gamma,diag(Q),H(1,:),R(1,1),'T');P1_pre=U1*[D1(1,1),0;0,D1(2,1)]*U1';%时间更新;K1=P1*H'*pinv(R);xKF1(:,t) = xKF_pre1(:,t) + K1*(zMea(:,t)-H*xKF_pre1(:,t));%距离估计[U2,D2]=UDKF(U2,D2,Phi,Gamma,diag(Q),H(1,:),R(1,1),'M');P1=U2*[D2(1,1),0;0,D2(2,1)]*U2';%量测更新;
end
%% errUD=P1-U*diag(D)*U';
function [U,D]=UDKF(U,D,Phi,Gamma,Q,H,R,TM)  %UD分解滤波
n=length(U); 
if ~ isempty(strfind(upper(TM),'T')) %isempty（A）为空，返回1；upper变为大写
C=[Phi*U,Gamma]; D1=[D;Q];  %D,Q为向量,D1是取D和Q对角元
A=0;
for j=n:-1:1  %时间更新D(j)=(C(j,:).*C(j,:))*D1;for i=1:(j-1)U(i,j)=(C(i,:).*C(j,:))*D1/D(j);C(i,:)=C(i,:)-U(i,j)*C(j,:);A=A+1;endA=A+1;
endend
if ~ isempty(strfind(upper(TM),'M'))f=(H*U)';g=D.*f; afa=f'*g+R;B=0;for j=n:-1:1  %量测更新afa0=afa-f(j)*g(j);lambda=-f(j)/afa0;D(j)=afa0/afa*D(j);afa=afa0;for i=1:(j-1)s=(i+1):(j-1);U(i,j)=U(i,j)+lambda*(g(i)+U(i,s)*g(s));B=B+1;endB=B+1;end
end
end
%UD分解
function[U,D]=myudut(P0)
n=length(P0);
U=eye(n);D=zeros(n,1);trPn=trace(P0)/n*1e-40;
for j=n:-1:1k=(j+1):n;D(j)=P0(j,j)-(U(j,k).^2)*D(k);if D(j)<=trPn,continue;endfor i=(j-1):-1:1U(i,j)=(P0(i,j)-(U(i,k).*U(j,k))*D(k))/D(j);end
end
end

4、遗忘滤波
经过长时间滤波后，滤波的增益计算回路一般会逐渐收敛，滤波增益K减小，使得滤波器的惯性不断增大，新的量测量对状态估计器的作用逐渐衰减。这时候，如果实际系统建模存在误差，滤波器容易出现虚的过度收敛现象。为了避免这种情况，在滤波过程中刻意改变过程噪声Qk和量测噪声Rk的权重，起到减小历史信息权重的作用。
在这里插入图片描述
s是略大于1的实数比例因子
看代码：

clear;clc;clear all;
%% 初始化参数
T = 600; N = 600;               % 仿真时长
qt = 0.1;                   % 过程噪声 ，单位m^2/s^3
Rk = 50^2;                    % 量测噪声,单位m^2
T_mea = 0.5;               % 量测采样时间
Qk = qt*T_mea;                %单位m^2/s^2
W =randn(1,T);
V =randn(1,T); 
s=1.05;   %设置遗忘滤波比例因子
% for k=1:T
% W(k)=sqrt(Qk)*W(k);  %设置遗忘滤波中过程噪声
% V(k)=sqrt(s^(T-k+1)*Rk)*V(k);  %设置遗忘滤波中量测噪声
% end
W=sqrt(Qk)*W;  %设置遗过程噪声
V=sqrt(Rk)*V;  %设置量测噪声
% 系统矩阵
phi = [1 -0.5;0 1];            % 状态矩阵
I = eye(2);
H = [1,0];                 % 量测矩阵
gamma = [0;1];
%% 初始化与分段状态方程书写
x = zeros(2, N);         %产生2*N的零矩阵
x0 = zeros(2, N);   %真实状态
z = zeros(1, N);
x(:,1) = [100000; 280];    %导弹实际数据，
x0(:,1) = [100000; 280];   %初值
z(:,1) = H*x(:,1) + V(:,1);     %量测系统离散化赋初值
% 状态方程分段编写
for i=2:100x0(:,i) = phi*x0(:,i-1) + gamma*W(i-1);
end
for i=100:200x0(:,i)=phi*x0(:,i-1)+gamma*W(i-1)+[0;-1]*1;
end
for i=200:Nx0(:,i) = phi*x0(:,i-1) + gamma*W(i-1);  
end
for i=2:Nx(:,i) = phi*x(:,i-1) + gamma*W(i-1);   z(i) = H*x0(:,i) + V(i);  %雷达量测方程不变
end
%% 状态估计               %卡尔曼滤波的初值和均方误差阵可以随便设值，均方误差阵是对称阵
X = zeros(2,N);  %卡尔曼滤波状态
X1= zeros(2,N);  %遗忘滤波状态
P = zeros(2,2,N);        %P是2*2*N的矩阵
X(:,1) = [100000; 280];   %雷达估计数据
X1(:,1) = [100000; 280];
P(:,:,1) = [1 0;0 1];
P1(:,:,1) = [1 0;0 1];
%% 卡尔曼滤波模型  估计都是按公式迭代的
for i=2:NX(:,i)=phi*X(:,i-1);P(:,:,i)=phi*P(:,:,i-1)*phi'+gamma*Qk*gamma';K=P(:,:,i)*H'/((H*P(:,:,i)*H'+Rk));  X(:,i)=X(:,i)+K*(z(i)-H*X(:,i));P(:,:,i)=(I-K*H)*P(:,:,i);
end
%% 遗忘滤波
for i=2:NX1(:,i)=phi*X1(:,i-1);P1(:,:,i)=phi*P1(:,:,i-1)*phi'+gamma*s^(N-i)*Qk*gamma';K1=P1(:,:,i)*H'/((H*P(:,:,i)*H'+s^(N-i)*Rk)); X1(:,i)=X1(:,i)+K1*(z(i)-H*X1(:,i));P1(:,:,i)=(I-K1*H)*P1(:,:,i);
end

5、信息滤波
在这里插入图片描述
简单来说，信息滤波就是将常规kalman式子全部用 I 表示。
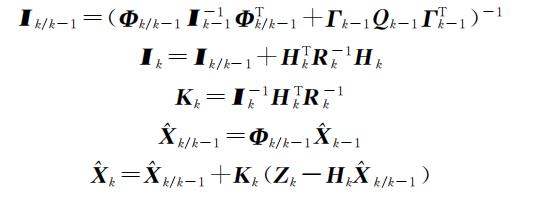
在这里插入图片描述
看代码：

clc;clear;clear all;
d0=100000;
v0=280;
q0=0.1;
f0=5;
r01=50;
r02=1;
%数据处理
length1=ceil(f0*d0/v0)+f0*50;%估计数据的数量
t=zeros(1,length1);%时间
s=zeros(1,length1);%导弹运动的距离
dl=zeros(1,length1);dl(1)=d0;%雷达观测距离
v=zeros(1,length1);v(1)=v0;%导弹速度
Ts=1/f0;%采样时间间隔
for i=1:length1t(i)=(i-1)*Ts;
end
for j=2:length1s(j)=s(j-1)+v(j-1)*Ts;v(j)=v(j-1)+sqrt(q0*Ts)*randn(1);dl(j)=d0-s(j)+sqrt(r01^2)*randn(1);%量测距离if d0-s(j)<0breakend
end
t=t(1,1:j);s=s(1,1:j);dl=dl(1,1:j);v=v(1,1:j);%更新数据
vl=v+sqrt(r02^2)*randn(1);%雷达观测速度
%信息滤波
XI2=zeros(2,j);PI21=zeros(j,1);PI22=zeros(j,1);%存储滤波得到的数据
XI2(:,1)=[0 280]';PI21(1)=2500;PI22(1)=100;%初值
phiI=[1 0.2;0 1];gammaI=[0 1]';QI=q0*Ts;RI=diag([r01^2 r02^2]);HI=[1 0;0 1];
for m=2:jXI1=XI2(:,m-1);PI1=[PI21(m-1) 0;0 PI22(m-1)];ZIx=[100000-dl(m-1);vl(m-1)];[XI,PI]=Information(phiI,gammaI,QI,RI,HI,XI1,PI1,ZIx);XI2(1,m)=XI(1);XI2(2,m)=XI(2);PI21(m)=PI(1,1);PI22(m)=PI(2,2);
end
function [ Xk, Pk ] = Information( phi,gamma,Q,R,H, X1,P1,Zk)l=length(X1); 
I=inv(P1);
S1=I*X1;
Mk1=inv(phi')*I*inv(phi);%1
Nk1=Mk1*gamma*inv(gamma'*Mk1*gamma+inv(Q))*gamma';%2
Ik1=(eye(l)-Nk1)*Mk1;%3
Ik=Ik1+H'*inv(R)*H;%4
Sk1=(eye(l)-Nk1)*inv(phi')*S1;%5
Sk=Sk1+H'*inv(R)*Zk;%6
Xk=inv(Ik)*Sk;
Pk=inv(Ik);end

6、自适应滤波
题目大意同上面，但这里假设零均值 测量噪声的方差是未知时变的，第一种情况， 1-100s 方差为 100m2,100s 之后为10000m2，并 且在 150s 时雷达出现一次量测故障使雷达输出 为 0；

自适应滤波算法可以通过量测输出在线实时地估计系统的噪声参数，可以进行故障检测和强跟踪。
在这里插入图片描述
针对上面问题，代码如下：

clear;clc;clear all;
N=600;%仿真次数
Ts=0.5;%采样时间
%% 系统方程的离散化
%% 连续系统模型（连续时间线性随机系统）
F = [0 -1;0 0];   %连续系统中状态一步转移矩阵
G = [0; 1];       %连续系统中系统噪声分配矩阵
q=0.05;           %系统噪声方差强度
%% 离散系统模型（连续时间线性随机系统的等效离散化形式）
I = eye(2);       %二阶单位矩阵
phi = I + F*Ts;   %离散系统状态转移矩阵
gamma = G*Ts;     %离散系统噪声分配阵
Q = q/Ts;         %状态转移协方差 
%% 量测方程的离散化
%% 量测系统离散化模型
H=[1 0];          %量测矩阵
R(1)=100;
R1(1)=10000;
%% 噪声方程
W=sqrt(Q)*randn(1,N);   %系统噪声方程，randn(1,N)是产生一个1*N的标准正态分布的随机矩阵
V=randn(1,N);
V(1)=sqrt(R(1))*V(1);
%% 初始化与
x = zeros(2, N);         %产生2*N的零矩阵
z = zeros(1, N);
x(:,1) = [100000; 280];    %导弹实际数据，：  
z(1) = H*x(:,1) + V(1);     %量测系统离散化方程
for i=2:100R(i)=100;
end
for i=100: NR(i)=10000;
end
for i=2:NV(i) =sqrt(R(i))*V(i);   %量测噪声方程
endfor i=2:149x(:,i) = phi*x(:,i-1) + gamma*W(i-1);   z(i) = H*x(:,i) + V(i);
end
for i=150x(:,i) = phi*x(:,i-1) + gamma*W(i-1);   z(i) = 0;
end
for i=151:Nx(:,i) = phi*x(:,i-1) + gamma*W(i-1);   z(i) = H*x(:,i) + V(i);
end
%% 状态估计              
X = zeros(2,N); 
X1= zeros(2,N);
Z = zeros(1,N);
c = zeros(1,N);
C = zeros(1,N);
P = zeros(2,2,N);        %P是2*2*N的矩阵
b=0.99;  %设置减消因子 常用0.9~0.999
c(1)= 1;  %
X(:,1) = [100000; 280];   %雷达估计数据
X1(:,1) = [100000; 280];
P(:,:,1) = [1 0;0 1];%% kalman滤波方程（离散时间系统的kalman滤波方程）
for i=2:NX(:,i)=phi*X(:,i-1);P(:,:,i)=phi*P(:,:,i-1)*phi'+gamma*Q*gamma';K=P(:,:,i)*H'/(H*P(:,:,i)*H'+R(i));  X(:,i)=X(:,i)+K*(z(i)-H*X(:,i));P(:,:,i)=(I-K*H)*P(:,:,i);
end%% 自适应滤波方程
for i=2:NX1(:,i)=phi*X1(:,i-1);P(:,:,i)=phi*P(:,:,i-1)*phi'+gamma*Q*gamma';Z(i)=z(i)-H*X1(:,i);c(i) = c(i-1)/(c(i-1)+b);R1(i)=(1-c(i))*R(i-1)+c(i)*(Z(i)*Z(i)'-H*P(:,:,i)*H');C(i)=(1-c(i))*C(i-1)+c(i)*Z(i)*Z(i)';if(trace(C(i))<10*trace((H*(phi*P(:,:,i-1)*phi'+gamma*Q*gamma')*H'+R1(i))))K=P(:,:,i)*H'/(H*P(:,:,i)*H'+R1(i)); X1(:,i)=X1(:,i)+K*(z(i)-H*X1(:,i));P(:,:,i)=(I-K*H)*P(:,:,i);end
end

感谢各位看官!撒花！


http://www.ppmy.cn/news/806729.html

相关文章

UUID?

UUID?

通用唯一识别码&#xff08;英语&#xff1a;Universally Unique Identifier&#xff0c;缩写&#xff1a;UUID&#xff09;是用于计算机体系中以识别信息的一个128位标识符。 UUID按照标准方法生成时&#xff0c;在实际应用中具有唯一性&#xff0c;且不依赖中央机构的注册和分…
阅读更多...
vue+Element 设置头部固定，并解决遮罩层显示问题

vue+Element 设置头部固定，并解决遮罩层显示问题

通过整体框架代码可以看到&#xff0c;其实element-ui已经实现了头部固定 找到这个fixedHeader&#xff0c;发现直接在全局设置文件里 这里如果设置为false&#xff0c;就表示头部不固定&#xff1b;改为true&#xff0c;则表示头部固定。 上述更改完后&#xff0c;就可以实…
阅读更多...
UD三分区补充教程1——激活不同分区对于UD三分区bios启动和uefi启动兼容性影响的讨论

UD三分区补充教程1——激活不同分区对于UD三分区bios启动和uefi启动兼容性影响的讨论

2015年08月01日 UD三分区补充教程1——激活不同分区对于UD三分区bios启动和uefi启动兼容性影响的讨论 UD三分区UD区ntfs数据区fat格式的高端efi 目前在测试UD三分区的过程中&#xff0c;特别是简化型三分区&#xff08;UD区只放grldr&#xff0c;其它全放efi区&#xff09;&…
阅读更多...
捷联惯导系统学习6.4(UD分解滤波 )

捷联惯导系统学习6.4(UD分解滤波 )

UD(unit upper traingular& diagonal factorization)分解滤波 UD(unit upper traingular& diagonal factorization)分解 P : n 阶 正 定 的 对 称 矩 阵 P:n阶正定的对称矩阵 P:n阶正定的对称矩阵 对矩阵P进行上三角-对角分解: U : 上 三 角 阵 U:上三角阵 U:上三角…
阅读更多...
分别使用U+、B+、UD制作WinPE启动盘

分别使用U+、B+、UD制作WinPE启动盘

同步在个人博客&#xff1a;https://www.zhyong.cn/posts/bb8d/ 最近看了女娲工坊的关于系统启动相关的视频&#xff0c;以及U盘启动制作的三种方式并进行了实践&#xff0c;学到了很多&#xff0c;在此记录。 什么是WinPE Windows预安装环境&#xff08;Microsoft Windows P…
阅读更多...
SAP QM 取消UD方法

SAP QM 取消UD方法

一、业务场景 1、 适用业务 通常检验批作完检验结果录入后,最后一步就是做UD判断,这一步的内容主要包括两方面:选定UD代码,表示检验将作如何的判定,如A表示接受,R表示拒绝,A1表示让步接受…&#xff1b;另外就是做库存转移&#xff0c;就是将检验状态的库存移为非限制状态的库…
阅读更多...
DPU是什么？

DPU是什么？

一、什么是DPU DPU(Data Processing Unit)数据中心处理器&#xff0c;采用软件定义技术路线支撑基础设施层资源虚拟化&#xff0c;支持存储、安全、服务质量管理等基础设施服务。   2020年,NVIDA公司将DPU定位为继CPU和GPU之后的“第三颗主力芯片”。DPU的出现&#xff0c;是…
阅读更多...
SAP UD取消处理合订本

SAP UD取消处理合订本

文章目录 一、QM检验批UD之后&#xff0c;还有后悔药吗&#xff1f;二、取消UD方法三、SAP Notes 74638—取消检验批UD判定四、SAP Notes 175842—取消检验批的库存过账 一、QM检验批UD之后&#xff0c;还有后悔药吗&#xff1f; 在QM UD之前发现错误&#xff0c;只要用MBST冲…
阅读更多...
最新文章

Copyright @ 2022~2023