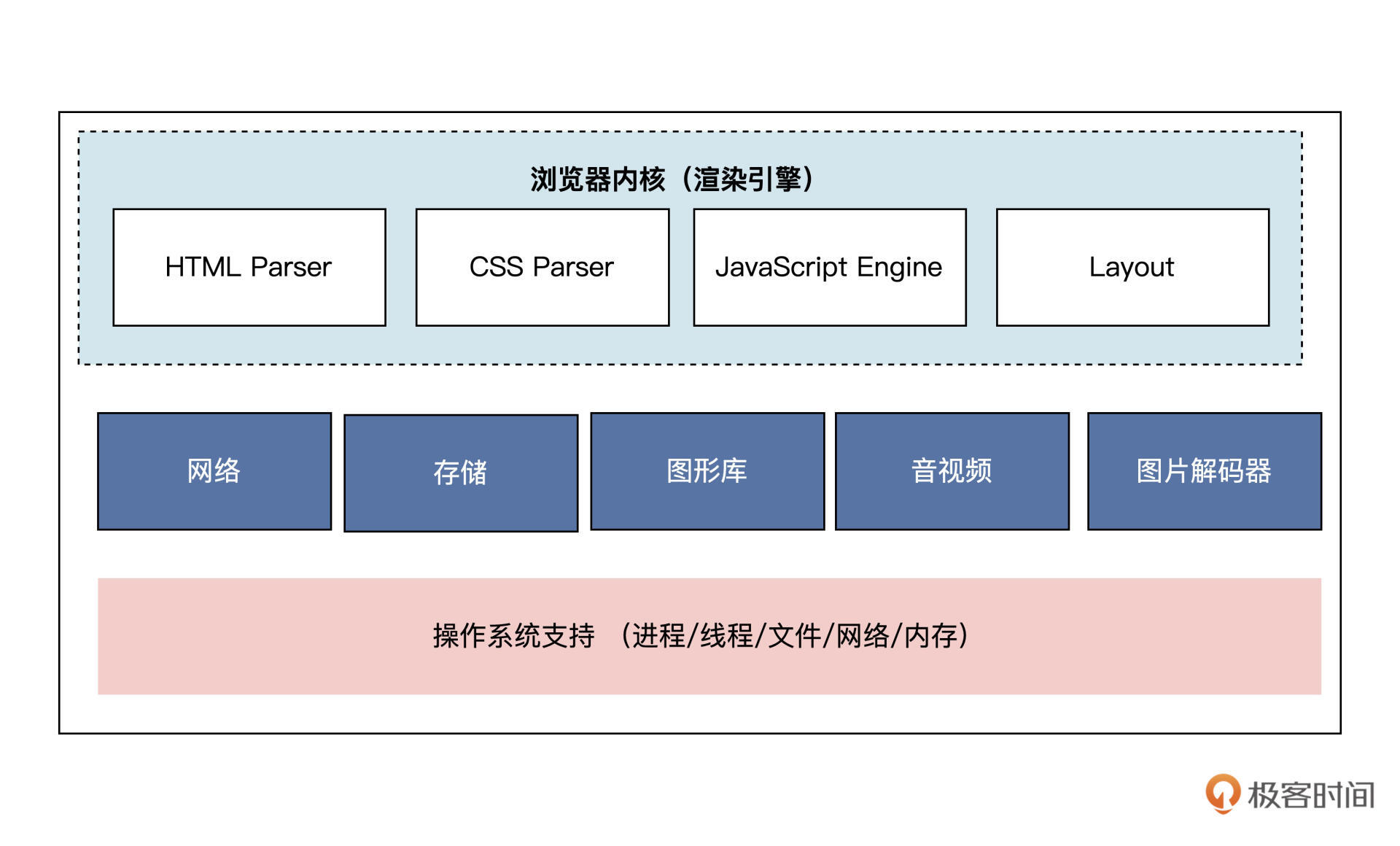
Convert to Base -2 负二进制转换

问题描述：

给你一个整数 n ，以二进制字符串的形式返回该整数的负二进制（base -2）表示。

注意，除非字符串就是 “0”，否则返回的字符串中不能含有前导零。

简单来说就是将一个十进制的n，转换成为负二进制的字符串。

n范围[0,10^9]

分析

对于十进制的n来说，
$x_1\times(10)^{0}+x_2\times(10)^{1}+x_3\times(10)^{2}+\dots+x_i\times(10)^{i-1}$ ,而每一位的数字范围为0~9，其表示形式就是每一位都是 $x_i$ ， $x_i$ 的范围[0,9].
对于同样的数值来说，十进制和二进制，或者N进制，都是不同的表示形式，其最终所代表的数值，是相同的。
所以以十进制的n来表示这样的数值，那么n的二进制就是

$x_1\times(2)^{0}+x_2\times(2)^{1}+x_3\times(2)^{2}+\dots+x_i\times(2)^{i-1}$ 变化的就是位权.
因此将十进制转换为二进制,就是求余,因为2的特点,二进制每一位只会是0,1.具体写法可以百度.
而十进制转换为x进制,其实与二进制相似, 用 c 表示x进制最低位的余数， $n = X * b + C$ . c的范围[0,x).*

但是负进制需要特殊的处理，n的负二进制， $x_1\times(-2)^{0}+x_2\times(-2)^{1}+x_3\times(-2)^{2}+\dots+x_i\times(-2)^{i-1}$ ,
$n = (- 2) * b + c$ , b和c都是整数，对于负二进制来说，每一位上的数值范围(-2,0],即-1,0。但是由于编程语言不同其意义就相差甚远。
在数学角度上模运算 $\mod Y = X -Y\times\lfloor X/Y \rfloor$ ,
$\mod y < y, y>0$
$\mod y > y, y<0$

但是在JAVA中一般会使用%处理模运算，但这个运算符实际上是求余的，对于普通的场景下求余和求模的结果是一样的，但是类似这个问题中，y<0,%计算的结果就是-1,0,1。
所以就需要特殊的处理。
但是实际表示中不会用-1来表示，而是使用高位+1和当前位为1的组合表示。
如果 $c = - 1, n = (- 2) * b + (- 1) => n = (- 2) * (b + 1) + 1$ ,这个处理就是负X进制的区别。

代码

public String baseNeg2(int n) {if (n == 0) {return "0";} int base = -2;StringBuilder sb = new StringBuilder();while(n!=0){            int r = n%base;                   String s = r==0?"0":"1";if(r!=0){                 n-=1;}sb.append(s);            n/=-2;}int p = sb.length()-1;while(p>0&&sb.charAt(p)=='0') sb.deleteCharAt(p--);sb.reverse();return sb.toString();}