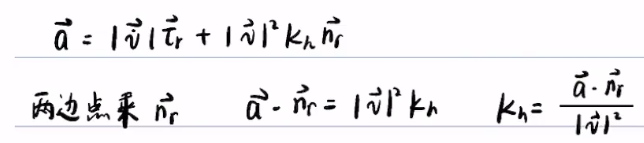1. 最速下降法

数值求解极小值问题的基本思想在于从给定的初始点 ${\vec{x}}_0$ 出发，沿某一搜索方向 ${\vec{d}}_0$ 进行搜索，同时通过确定最佳步长 ${\alpha }_0$ 使函数值沿该搜索方向下降最大。依此方式不断进行，形成函数值下降的迭代算法，即：
$$\begin{gathered} {\vec{x}}_{k+1}={\vec{x}}_k+{\alpha }_k{\vec{d}}_k(k=0,1,2,\dots ) \\ f({\vec{x}}_{k+1})<f({\vec{x}}_k) \end{gathered}$$
对于任意的 $n$ 元函数 $f(\vec{x})(\vec{x}\in {\mathbb{R}}^n)$ 的方向导数（反映函数在当前位置沿任意方向的变化快慢）：
$$\begin{array}{rl}& {\frac{df(\vec{x})}{d\vec{r}}|}_{\vec{x}={\vec{x}}_0}=\underset{\Delta r\to 0}{\lim }\frac{f(x_1+\Delta x_1,x_2+\Delta x_2,\dots ,x_n+\Delta x_n)-f(x_1,\dots ,x_n)}{\Delta r}\\ & \\ & ={grad(f)|}_{\vec{x}={\vec{x}}_0}\cdot \vec{r}\end{array}$$
其中，$\vec{r}=\frac{1}{\Delta r}\left[\begin{array}{c}\Delta x_1,\Delta x_2,\dots ,\Delta x_n\end{array}\right]$ 为任意单位方向，$\Delta r=\sqrt{\Delta x_1^2+\cdots +\Delta x_n^2}$，

上式说明：函数的负梯度方向是函数值在该点下降最快的方向。 因此，很容易想到利用负梯度作为搜索方向，这便是为何将其称为最速下降法（Steepest Descent）或梯度法，即
$${\vec{x}}_{k+1}={\vec{x}}_k-{\alpha }_k▽f({\vec{x}}_k)(k=0,1,2,\dots )$$
搜索方向确定后，步长还有待确定。我们希望函数沿着搜索方向上能够“前进”到该方向上的极小值，如图所示：

换而言之，每步搜寻所采取的最佳步长 $\alpha$ 的确定是通过在搜索方向上进行一维极小值问题的求解 (试探法，插值法…) 获得，即
$$\underset{\alpha }{\min }f[{\vec{x}}_k-\alpha ▽f({\vec{x}}_k)]=\underset{\alpha }{\min }\varphi (\alpha )$$
根据一元极值问题的必要条件：
ϕ ′ ( α ) = − { ▽ f [ x ⃗ k − α ▽ f ( x ⃗ k ) ] } T ⋅ [ ▽ f ( x ⃗ k ) ] = − [ ▽ f ( x ⃗ k + 1 ) ] T ⋅ [ ▽ f ( x ⃗ k ) ] = 0 \phi'(\alpha)=-\{\bigtriangledown f[\vec{x}_k-\alpha\bigtriangledown f(\vec{x}_k)]\}^T\cdot[\bigtriangledown f(\vec{x}_k)]=-[\bigtriangledown f(\vec{x}_{k+1})]^T\cdot[\bigtriangledown f(\vec{x}_k)]=0 ϕ′(α)=−{▽f[x k​−α▽f(x k​)]}T⋅[▽f(x k​)]=−[▽f(x k+1​)]T⋅[▽f(x k​)]=0
这说明了在最速下降法中， 相邻两个迭代点上的函数梯度相互垂直，即相邻两个搜索方向互相垂直 ，形成“之”字形的直齿锯齿现象。

由于锯齿现象，当迭代点接近极小点时，搜索的步长变得越来越小，因而收敛速度减慢，这种情况似乎与“最速下降”的名称相矛盾，这主要是因为梯度是函数的局部性质 （从局部上看，在一点附近函数的下降是快的），但从整体上看则走了许多弯路，函数的下降并不算快。不过最速下降法最初的几步往往可以下降的较快。

2. 抛物型多元二次函数优化问题的步长选取

对于抛物型多元二次函数：
$$g(\vec{x})=\frac{1}{2}{\vec{x}}^T\mathbf{A}\vec{x}-{\vec{b}}^T\vec{x}+c（\mathbf{A}\in SPD;c\in \mathbb{R}）$$
若采用最速下降法求解其最小值：

• 搜索方向：
  $$-▽g=-\mathbf{A}{\vec{x}}_k+\vec{b}={\vec{r}}_k$$
  其中，${\vec{r}}_k$ 为迭代法求解线性方程组 $\mathbf{A}\vec{x}=\vec{b}$ 第 $k$ 步的残差。

• 搜索路径：
  $$\begin{gathered} {\vec{x}}_{k+1}={\vec{x}}_k+{\alpha }_k{\vec{r}}_k \\ {\vec{r}}_{k+1}^T\cdot {\vec{r}}_k=0 \end{gathered}$$

对于这种情况，在求解最佳步长时，可以不用在搜索方向上进行一维搜索的数值计算，可以通过理论的方式直接推导出 ${\alpha }_k$ 的计算表达式：
$${\alpha }_k=\frac{{\vec{r}}_k^T\cdot {\vec{r}}_k}{{\vec{r}}_k^T\cdot \mathbf{A}\cdot {\vec{r}}_k}$$

证明：
$$\begin{array}{rl}& 0={\vec{r}}_{k+1}^T\cdot {\vec{r}}_k\\ & \\ & =(\vec{b}-\mathbf{A}\cdot {\vec{x}}_{k+1}{)}^T\cdot {\vec{r}}_k\\ & \\ & =[\vec{b}-\mathbf{A}\cdot ({\vec{x}}_k+{\alpha }_k{\vec{r}}_k){]}^T\cdot {\vec{r}}_k\\ & \\ & =[(\vec{b}-\mathbf{A}\cdot {\vec{x}}_k)-{\alpha }_k\mathbf{A}\cdot {\vec{r}}_k){]}^T\cdot {\vec{r}}_k\\ & \\ & ={\vec{r}}_k^T\cdot {\vec{r}}_k-{\alpha }_k{\vec{r}}_k^T\cdot \mathbf{A}\cdot {\vec{r}}_k\\ & \end{array}$$
故，
$${\alpha }_k=\frac{{\vec{r}}_k^T\cdot {\vec{r}}_k}{{\vec{r}}_k^T\cdot \mathbf{A}\cdot {\vec{r}}_k}(\ast )$$

综上所述，上述多元二次函数的优化问题的求解格式为：

1. ${\vec{r}}_k=\vec{b}-\mathbf{A}\cdot {\vec{x}}_k$

2. ${\vec{x}}_{k+1}={\vec{x}}_k+\frac{{\vec{r}}_k^T\cdot {\vec{r}}_k}{{\vec{r}}_k^T\cdot \mathbf{A}\cdot {\vec{r}}_k}{\vec{r}}_k$

其中，$k=0,1,2,3\dots$

最后指出，上述求解格式也可用于求解非多元二次函数的其他函数的优化问题，这是因为，根据多元泰勒展开式：
$$f(\vec{x})=f({\vec{x}}_0)+▽[f({\vec{x}}_0){]}^T\cdot (\vec{x}-{\vec{x}}_0)+\frac{1}{2}(\vec{x}-{\vec{x}}_0{)}^T\cdot \mathbf{H}({\vec{x}}_0)\cdot (\vec{x}-{\vec{x}}_0)+\dots$$
其中，海塞矩阵
$$\mathbf{H}({\vec{x}}_0)=\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1^2}& \frac{{\partial }^{2}f}{\partial x_1\partial x_2}& \dots & \frac{{\partial }^{2}f}{\partial x_1\partial x_n}\\ & & & \\ \frac{{\partial }^{2}f}{\partial x_2\partial x_1}& \frac{{\partial }^{2}f}{\partial x_2^2}& \dots & \frac{{\partial }^{2}f}{\partial x_2\partial x_n}\\ & & & \\ ⋮& ⋮& & ⋮\\ & & & \\ \frac{{\partial }^{2}f}{\partial x_n\partial x_1}& \frac{{\partial }^{2}f}{\partial x_n\partial x_2}& \dots & \frac{{\partial }^{2}f}{\partial x_n^2}\end{array}\right]$$
这说明在局部上，函数均可通过二次函数进行近似，即
$$\{\begin{array}{l}\mathbf{A}\approx \mathbf{H}({\vec{x}}_0)\\ \\ \vec{b}\approx ▽[f({\vec{x}}_0)]\\ \\ c\approx f({\vec{x}}_0)\end{array}$$

3. 抛物型多元二次函数等值线/面的几何分析

前述抛物型多元二次函数的等值线、等值面方程为：
$$\frac{1}{2}{\vec{x}}^T\mathbf{A}\vec{x}-{\vec{b}}^T\vec{x}+c=\beta ,(A为正定/负定对称矩阵，\beta \in [\min f,\max f])$$
将上述一般形式转变为标准形式：

• 平移变换：$\vec{x}=\vec{y}+{\vec{x}}_0$（其中，${\vec{x}}_0$ 为待定的常向量）
  $$\begin{array}{rl}& \frac{1}{2}{\vec{x}}^T\mathbf{A}\vec{x}-{\vec{b}}^T\vec{x}+c\\ & \\ & =\frac{1}{2}(\vec{y}+{\vec{x}}_0{)}^T\mathbf{A}(\vec{y}+{\vec{x}}_0)-{\vec{b}}^T(\vec{y}+{\vec{x}}_0)+c\\ & \\ & =\frac{1}{2}{\vec{y}}^T\mathbf{A}\vec{y}+{\vec{y}}^T(\mathbf{A}{\vec{x}}_0-\vec{b})+\frac{1}{2}{\vec{x}}_0^T\mathbf{A}{\vec{x}}_0-{\vec{b}}^T{\vec{x}}_0+c(令{\vec{x}}_0={\mathbf{A}}^{-1}\vec{b})\\ & \\ & =\frac{1}{2}{\vec{y}}^T\mathbf{A}\vec{y}-\frac{1}{2}{\vec{b}}^T{\mathbf{A}}^{-1}\vec{b}+c=\beta \\ & \end{array}$$

• 旋转操作：$\vec{y}=\mathbf{Q}\vec{z}，{\mathbf{Q}}^{\mathbf{T}}\mathbf{AQ}=\mathbf{D}$ (正交合同)，其中，$\mathbf{A}$的特征对为 ${\vec{u}}_i-{\lambda }_i^A$
  $$\begin{array}{rl}& \mathbf{Q}=\left[\begin{array}{cccc}{\vec{u}}_1& {\vec{u}}_2& \dots & {\vec{u}}_n\end{array}\right]\\ & \\ & \mathbf{D}=\left[\begin{array}{ccccc}{\lambda }_1^A& & & & \\ & & & & \\ & & {\lambda }_2^A& & \\ & & & & \\ & & & \ddots & \\ & & & & \\ & & & & {\lambda }_n^A\end{array}\right]\end{array}$$
  则有：
  $$\begin{array}{rl}& \frac{1}{2}{\vec{x}}^T\mathbf{A}\vec{x}-{\vec{b}}^T\vec{x}+c\\ & \\ & =\frac{1}{2}{\vec{y}}^T\mathbf{A}\vec{y}-\frac{1}{2}{\vec{b}}^T{\mathbf{A}}^{-1}\vec{b}+c\\ & \\ & =\frac{1}{2}{\vec{z}}^T\mathbf{D}\vec{z}-\frac{1}{2}{\vec{b}}^T{\mathbf{A}}^{-1}\vec{b}+c=\beta \\ & \end{array}$$
  记
  $${\vec{z}}^T\mathbf{D}\vec{z}=\beta -2c+{\vec{b}}^T{\mathbf{A}}^{-1}\vec{b}\triangleq \alpha \{\begin{array}{l}>0(A为正定矩阵)\\ \\ <0(A为负定矩阵)\end{array}$$
  则
  $${\vec{z}}^T\mathbf{D}\vec{z}=\alpha ⟹\frac{z_1^2}{\frac{\alpha }{{\lambda }_1^A}}+\frac{z_2^2}{\frac{\alpha }{{\lambda }_2^A}}+\cdots +\frac{z_n^2}{\frac{\alpha }{{\lambda }_n^A}}=1$$
  其中，
  $$\vec{z}={\mathbf{Q}}^T(\vec{x}-{\mathbf{A}}^{-1}\vec{b})$$
  通过标准型可以较容易地知道“椭圆“ 的相关信息：

• $k$ 轴所在直线的一般方程（面的交线）为：
  $$z_i=0(i=1,2,\dots ,n且i\ne k)$$
  $k$ 轴对应的单位方向与 $z_i=0(i=1,2,\dots ,n且i\ne k)$ 定义的 $n-1$ 个平面的法线 ${\vec{u}}_i(i=1,2,\dots ,n且i\ne k)$ 正交，这说明 $k$轴所在方向即为特征向量 ${\vec{u}}_k$ 所在的方向。并且轴线方向不因等值面 $\beta$ 的不同而改变，即所有椭圆等值面的轴具有相同的方向且同心，这意味着倘若初始点任意选择，并不再选择负梯度方向作为搜索方向，而选择 $\mathbf{A}$ 的特征方向作为搜索方向（即平行于各轴进行搜索），那么至多 n 步便能寻得最小值。
  

• 各个半轴长为：
  $$a_i=\sqrt{\frac{\alpha }{{\lambda }_i^A}}$$
  即，某一特定的等值线，特征值越大的方向，椭圆越扁平

另外，梯度沿着等值线、等值面的外法线方向，那么轴线上的各点梯度便指向 ”椭圆“ 中心，说明：若初始点恰巧选择在 ”椭圆“ 的轴线，最速下降法仅一步便可以求得上述优化问题的解。

4. 基于最速下降法的 “变步长Richardson 迭代法” 的收敛性分析

求解线性方程组：
$$\mathbf{A}\vec{x}=\vec{b}(\mathbf{A}\in SPD)$$
等价于求解如下二次函数的极小值点：
$$g(\vec{x})=\frac{1}{2}{\vec{x}}^T\mathbf{A}\vec{x}-{\vec{b}}^T\vec{x}+c(\mathbf{A}\in SPD)$$
基于最速下降法可以得出 “变步长Richardson 迭代法”，即参数 $\alpha$ 不再取为固定值，求解格式如下：
$$\{\begin{array}{l}{\vec{r}}_k=\vec{b}-\mathbf{A}\cdot {\vec{x}}_k\\ \\ {\alpha }_k=\frac{{\vec{r}}_k^T\cdot {\vec{r}}_k}{{\vec{r}}_k^T\cdot \mathbf{A}\cdot {\vec{r}}_k}\\ \\ {\vec{x}}_{k+1}={\vec{x}}_k+{\alpha }_k{\vec{r}}_k\end{array}$$
现对这种方法的收敛性及收敛速度进行分析：(方程组的精确解为 $\vec{x}$)

令
$$\begin{array}{r}E({\vec{x}}_k)\triangleq \frac{1}{2}{\vec{e}}_k^T\mathbf{A}{\vec{e}}_k=\frac{1}{2}(\overrightarrow{x_k}-\vec{x}{)}^T\mathbf{A}(\overrightarrow{x_k}-\vec{x})=g({\vec{x}}_k)+\frac{1}{2}{\vec{x}}^T\mathbf{A}\vec{x}\end{array}$$
又
$$\begin{gathered} {\vec{x}}_{k+1}={\vec{x}}_k+{\alpha }_k{\vec{r}}_k⟹{\vec{e}}_{k+1}={\vec{e}}_k+{\alpha }_k{\vec{r}}_k \\ {\vec{r}}_k=\vec{b}-\mathbf{A}{\vec{x}}_k=\mathbf{A}\vec{x}-\mathbf{A}{\vec{x}}_k=-\mathbf{A}{\vec{e}}_k⟹{\vec{e}}_k=-{\mathbf{A}}^{-1}{\vec{r}}_k \end{gathered}$$
那么
$$\begin{array}{rl}& \frac{E({\vec{x}}_k)-E({\vec{x}}_{k+1})}{E({\vec{x}}_k)}\\ & \\ & =\frac{{\vec{e}}_k^T\mathbf{A}{\vec{e}}_k-{\vec{e}}_{k+1}^T\mathbf{A}{\vec{e}}_{k+1}}{{\vec{e}}_k^T\mathbf{A}{\vec{e}}_k}\\ & \\ & =\frac{{\vec{e}}_k^T\mathbf{A}{\vec{e}}_k-({\vec{e}}_k+{\alpha }_k{\vec{r}}_k{)}^T\mathbf{A}({\vec{e}}_k+{\alpha }_k{\vec{r}}_k)}{{\vec{e}}_k^T\mathbf{A}{\vec{e}}_k}\\ & \\ & =\frac{-2{\alpha }_k{\vec{r}}_k^T\mathbf{A}{\vec{e}}_k-{\alpha }_k^2{\vec{r}}_k^T\mathbf{A}{\vec{r}}_k}{{\vec{e}}_k^T\mathbf{A}{\vec{e}}_k}\\ & \\ & =\frac{({\vec{r}}_k^T{\vec{r}}_k{)}^2}{({\vec{r}}_k^T\mathbf{A}{\vec{r}}_k)({\vec{r}}_k^T{\mathbf{A}}^{-1}{\vec{r}}_k)}\\ & \\ & \ge \frac{4{\lambda }_{min}^A{\lambda }_{max}^A}{({\lambda }_{min}^A+{\lambda }_{max}^A{)}^2}（Kantorvich不等式）\end{array}$$
从而有：
$$E({\vec{x}}_{k+1})\le \left[1-\frac{4{\lambda }_{min}^A{\lambda }_{max}^A}{({\lambda }_{min}^A+{\lambda }_{max}^A{)}^2}\right]E({\vec{x}}_k)={\left(\frac{{\lambda }_{min}^A-{\lambda }_{max}^A}{{\lambda }_{min}^A+{\lambda }_{max}^A}\right)}^{2}E({\vec{x}}_k)$$
那么
$$0\le E({\vec{x}}_k)\le {\left(\frac{{\lambda }_{min}^A-{\lambda }_{max}^A}{{\lambda }_{min}^A+{\lambda }_{max}^A}\right)}^{2k}E({\vec{x}}_0)$$
即
$$\underset{k\to \infty }{\lim }E({\vec{x}}_k)=0$$
因为 $\mathbf{A}$ 为对称正定矩阵，当且仅当 ${\vec{x}}_k=\vec{x}$ 时，$E({\vec{x}}_k)=0$，故基于最速下降法的 “变步长Richardson 迭代法”必定收敛，且收敛速度至少为：
$${\left(\frac{{\lambda }_{min}^A-{\lambda }_{max}^A}{{\lambda }_{min}^A+{\lambda }_{max}^A}\right)}^2={\left[\frac{cond(\mathbf{A}{)}_2-1}{cond(\mathbf{A}{)}_2+1}\right]}^2$$
优于Richardson 迭代法的最佳收敛速度。

那么，当对称正定矩阵 $\mathbf{A}$ 的最大特征值越接近于最小特征值时，收敛速度越快，换而言之，等值线的椭圆长轴短轴长度越接近时收敛速度越快，最佳的情况是等值线为同心圆，此时仅需一步便可得到精确解。而若椭圆偏心率越大，越扁平，即最大特征值与最小特征值相差越大，收敛速度便会越小。