空间自相关指的是分布于不同空间位置的地理事物,它的某一个属性值存在统计相关性,一般来说,距离越近,相关性越大。
本次分析某一个城市的不同收入家庭的居住空间分布情况。
先用全局空间自相关指数(Moran’s指数)判断这个城市的家庭收入是否存在空间自相关;
如果存在,再使用高/低聚类判断是哪种类型的聚类;
最后,进行聚类和异常值分析以及热点分析,找出各类集聚的空间分布区域。
我们先打开一个城市的家庭收入面数据,可以简单看一下情况。
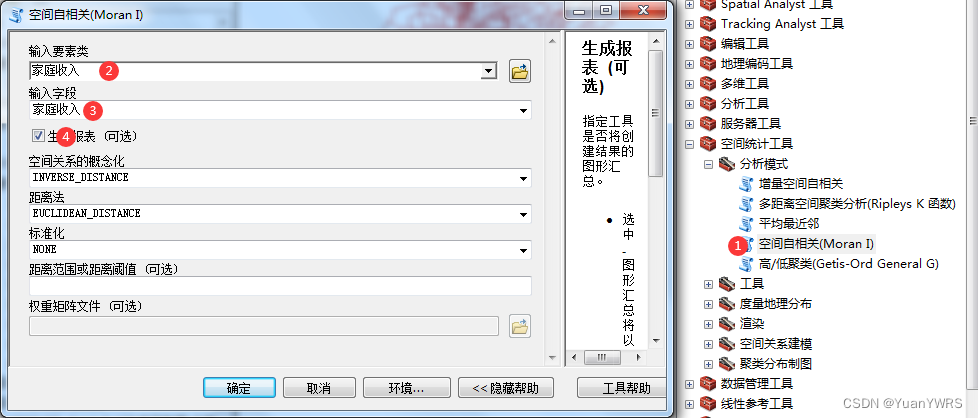
1:打开空间自相关工具(位于分析模式下)。、
2:输入数据。
3:选择字段,这里我们选择收入字段。
4:生成报表勾选了。
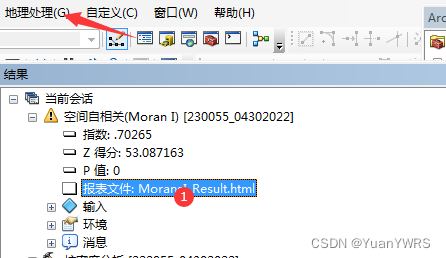
查看结果(在地理处理下。)
打开这个html文件。
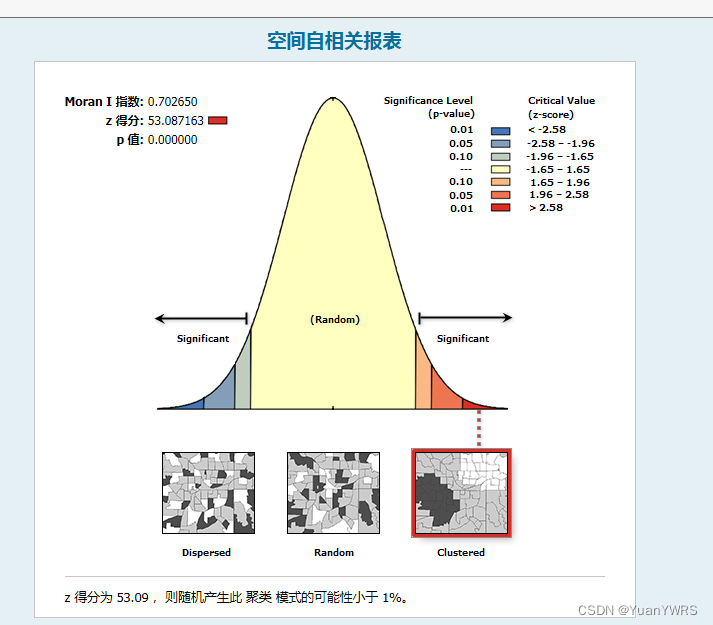
从结果图可知,Z为53.09,P值为0,表明,家庭收入空间分布存在比较显著的空间正相关。也就是出现了高与高收入家庭集聚,低与低收入家庭集聚(对应图中的红色部分)。
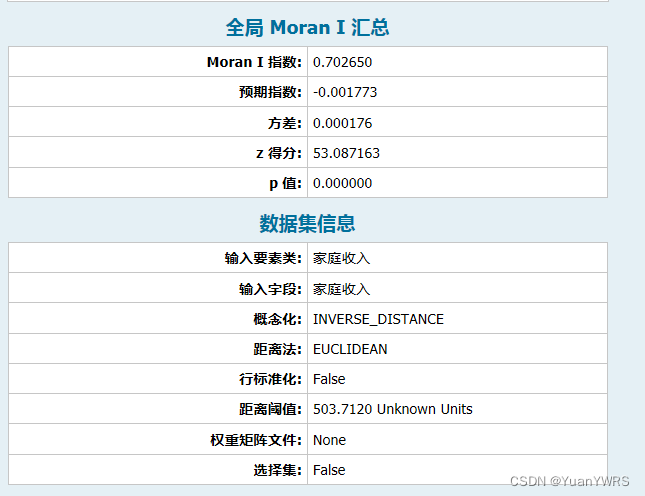
从上面的结果我们知道:Moran’s I指数不能判断到底是高与高还是低与低集聚。
因此,可以采用General G 进行判断(z得分为正表示高/高集聚,为负数就表示低/低集聚)。
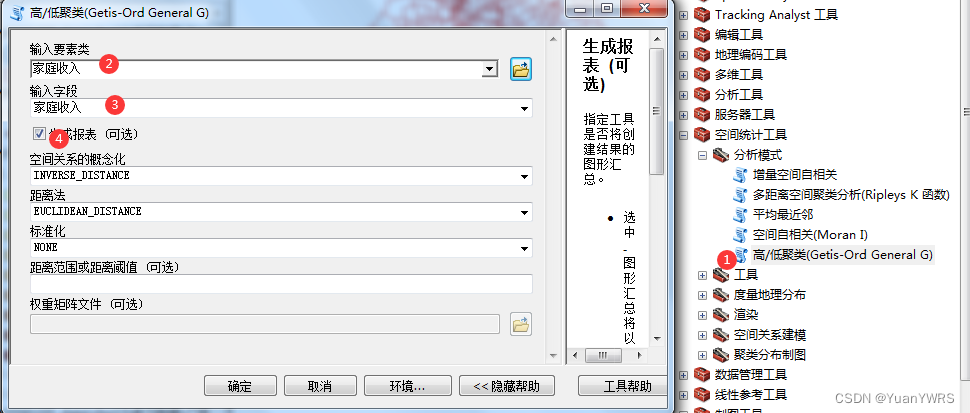
类似上述操作,
1:找到高/低聚类工具。
2:输入数据。
3:字段选择。
4:生成报表。
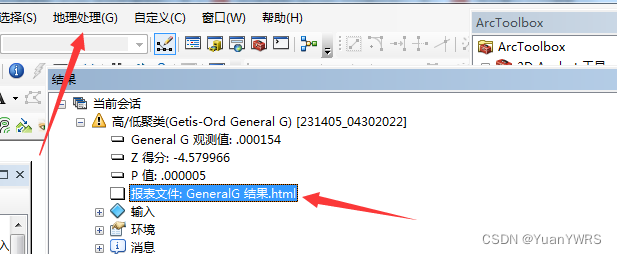
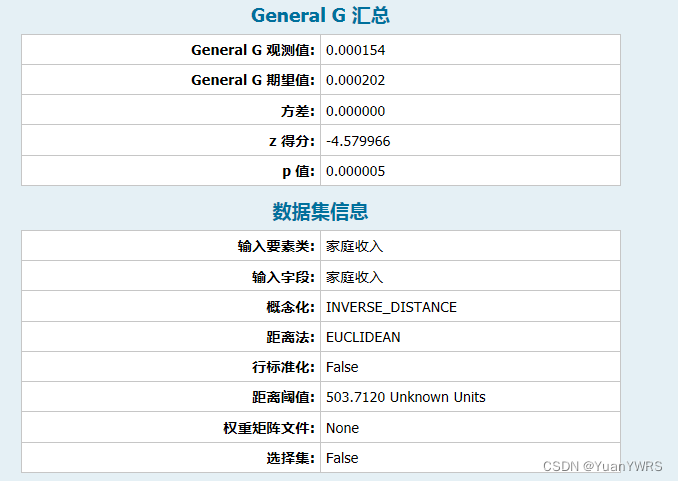
我们还是一样的查看结果。
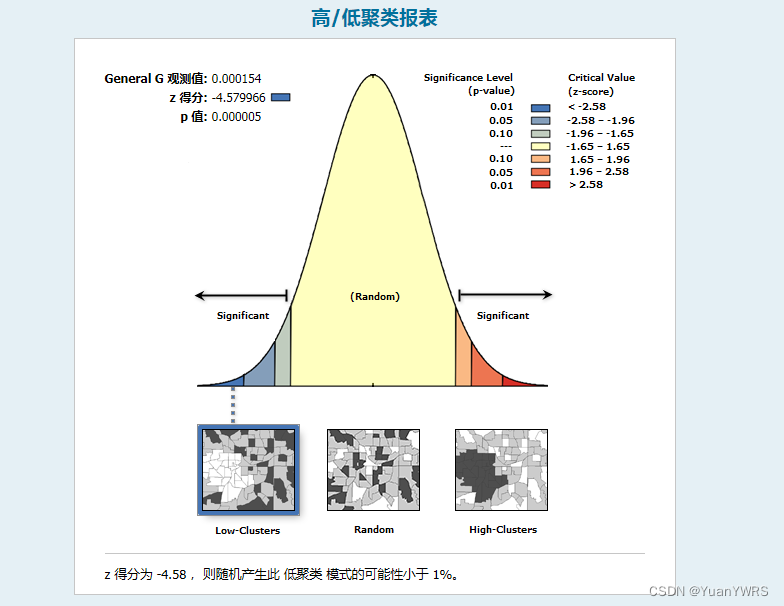
Z的得分为-4.58,也就是存在显著的低/低集聚的情况(上图蓝色区域)。
但是,数据本身存在这样一种情况:
空间事物存在异质性,在某些局部表现为空间正相关,另外一部分可能是发散的,因此,需要进行局域空间自相关。
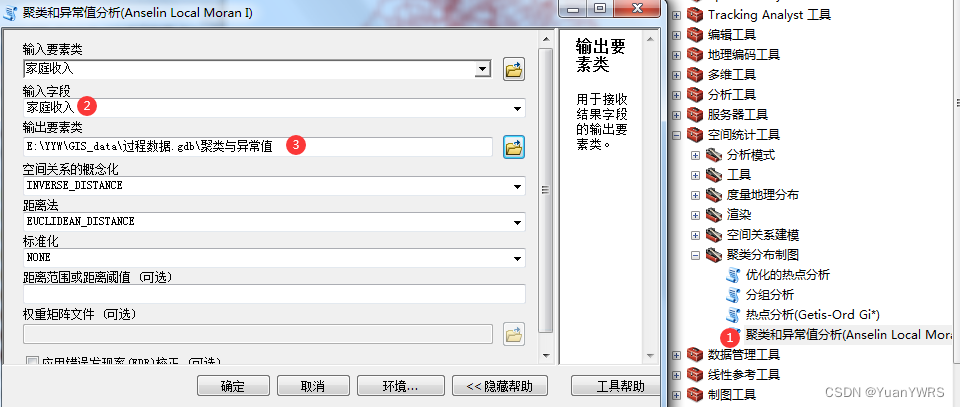
1:找到聚类和异常值分析工具(位于聚类分布制图下)。
2:输入字段。
3:输出地址与命名。
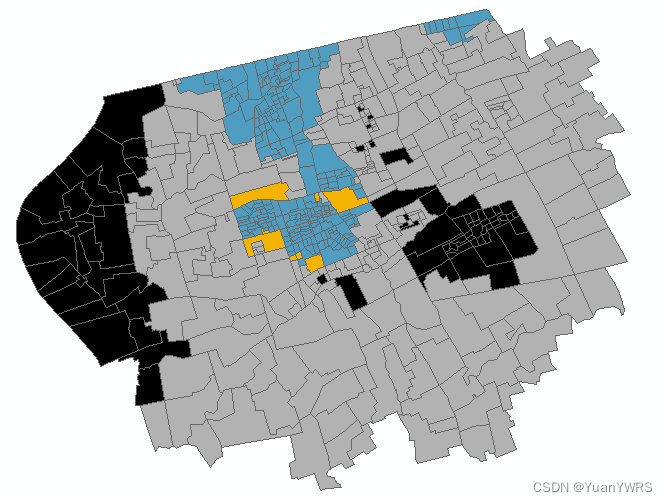

通过上图我们可以知道:
黑色区域是高/高集聚,主要分布在城市的西部和东部。
蓝色的是低/低集聚,主要分布在中部地区。
橙色是高/低集聚,数量和区域都很小。
下面进行热点分析:
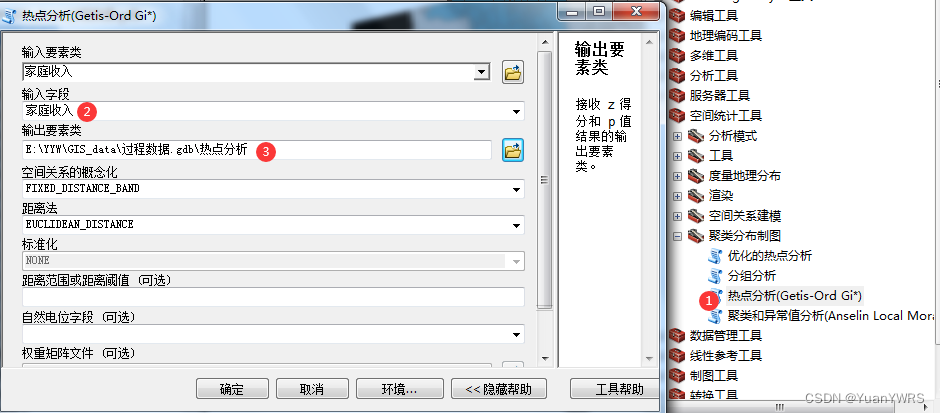
1:热点分析。
2:输入字段(家庭收入)。
3:输出地址。
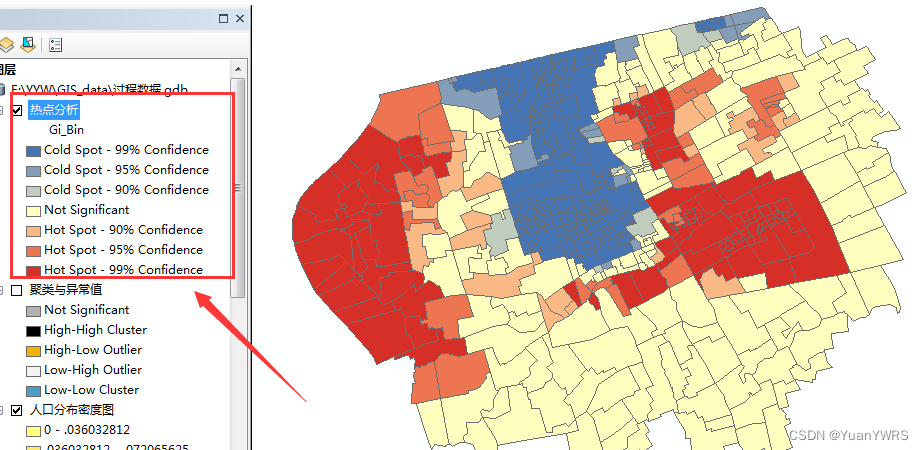
通过以上的分析可以得出结论:
这个城市存在高/高收入集聚和低/低收入集聚(更显著),表面城市空间存在居住分异现象,不利于城市的发展。







