- PWM示意图
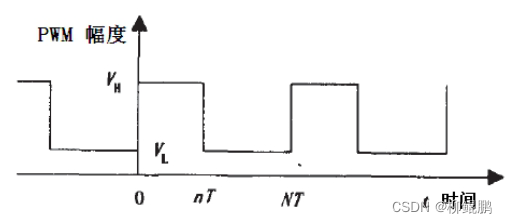
PWM 本质上其实就是一种周期一定,占空比可调的方波。典型PWM 波形如下
图所示:
- PWM分段函数
图中的PWM 波形可以用如下分段函数表示:
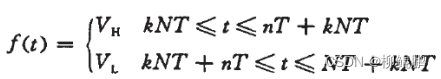
函数中:T 是单片机中计数脉冲的基本周期,也就是STM32F4 定时器的计数频率的倒数。N 是PWM 波一个周期的计数脉冲个数,也就是STM32F4 的ARR-1 的值。n 是PWM 波一个周期中高电平的计数脉冲个数,也就是STM32F4的CCRx 的值。VH 和VL 分别是PWM 波的高低电平电压值,k 为谐波次数,t 为时间。
- 傅里叶级数
我们将上式展开成傅里叶级数,可得到如下公式:
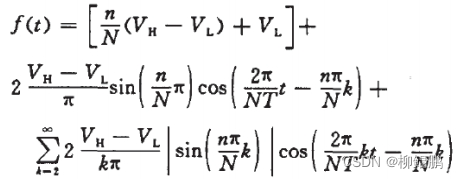
从公式中可以看出,第1 项为直流分量,第2 项为1 次谐波分量,第3 项为大于1 次的高次谐波分量。式中的直流分量与n 成线性关系,并随着n 从0到N,直流分量从VL 到VH 之间变化。这正是电压输出的DAC 所需要的。
因此,如果能把式中除直流分量外的谐波过滤掉,则可以得到从PWM 波到电压输出DAC 的转换,即:PWM 波可以通过一个低通滤波器进行解调。式中的第2 项的幅度和相角与n 有关,频率为1/(NT),其实就是PWM 的输出频率。该频率是设计低通滤波器的依据。如果能把1 次谐波很好过滤掉,则高次谐波就基本不存在了。



