1. 剑指 Offer 14- I. 剪绳子
题目描述:给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
1.1 方法一:动态规划
1.1.1 推导
- 求最大值问题可考虑使用动态规划算法解决;
- 动态规划解题的四大要素:状态定义、状态转移方程定义、初始状态以及返回结果;
- 针对剪绳子问题,目的是将一个长度为n的绳子划分为m段,m段绳子最大乘积是多少,其中m>1,也就是将绳子需至少划分为两段;
- 动态规划四要素:
1)状态F(i):长度为i的绳子,划分后最大乘积为F(i);
2)状态转移方程:F(i)=Max{F(i),F(i-j)*j,(i-j)*j};
3)初始状态:F(2)=1,长度为2的绳子至少划分为两段,因此每段长度为1;
4)返回结果:F(n),长度为n的绳子划分后的最大乘积; - 长度为n的绳子划分后最大乘积,可由长度小于n的绳子的划分最大乘积进一步得到。假设将绳子划分为两段,一段长度为j,另一段长度为n-j,长度为n-j的绳子可以进一步划分,也可以不划分,因此有对应两种情况:
1)n-j的绳子不再划分,则划分乘积为j*(n-j);
2)n-j的绳子继续划分,则划分乘积为j*F(n-j);
1.1.2 代码实现
class Solution {// 动态规划// 状态F(i):长度为i的绳子,划分后最大乘积为F(i)// 状态转移方程:F(i)=Max{F(i),F(i-j)*j,(i-j)*j}// 初始状态:F(2)=1public int cuttingRope(int n) {int[] maxPro=new int[n+1];// 初始状态maxPro[2]=1;// 状态转移for(int i=3;i<=n;i++){for(int j=1;j<i;j++){maxPro[i]=Math.max(maxPro[i],j*maxPro[i-j]);maxPro[i]=Math.max(maxPro[i],(i-j)*j);}}// 返回结果return maxPro[n];}
}
1.2 方法二:数学规律
1.2.1 数学推导
-
针对剪绳子问题,目的是将一个长度为n的绳子划分为a段,a段绳子最大乘积是多少,其中a>1,也就是将绳子需至少划分为两段;
-
假设将绳子划分为a段,分别为n1,n2,…,na,由下列算术几何均值不等式可知,当n1=n2=…=na时,n1,n2,…,na乘积最大;

-
由上述公式可知当将长度为n的绳子等长划分后,乘积最大。假设每段绳子长度为x,共划分为a段,则乘积为xa,a=n/x,进一步推导:
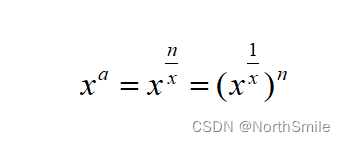
也就是当x1/x最大时,划分乘积最大,令y=x1/x,进行隐函数求导可得:

但我们知道绳子划分段长度需要为整数,则可取近似值x=3或x=2,分别将x代入y=x1/x可知当x=3时划分乘积最大; -
有上述推导可总结划分原则:
1)尽可能将绳子划分为长度为3的段,共t段,剩余绳子长度有0,1,2三种可能;
2)如果剩余绳子长度为0,说明绳子原长度正好为3的倍数,此时得到最优解3t;
3)如果剩余绳子长度为2,则将剩余部分看做整体,不再进一步划分,则划分乘积为3t*2;
4)如果剩余绳子长度为1,则将长度为3的子段取出一个与剩余部分总长度为4(将其划分为两段长度为2的子段,因为此时2*2>1*3),则划分乘积为3t-1*2*2;
参考https://leetcode.cn/problems/jian-sheng-zi-ii-lcof/solution/mian-shi-ti-14-ii-jian-sheng-zi-iitan-xin-er-fen-f/
1.2.2 代码实现
class Solution {// 数学推导:将绳子尽可能按照长度为3的段分割,乘积最大public int cuttingRope(int n) {if(n<=2){return 1;}// 特殊情况if(n==3){return 2;}int res=n/3; // 按照3分割,最多得到多少段int mod=n%3; // 只有0,1,2三种情况if(mod==0){return (int)Math.pow(3,res); // 说明是3的倍数}else if(mod==1){return (int)Math.pow(3,res-1)*4; // 3a+1,把最后两段3+1划分为2+2}else{return (int)Math.pow(3,res)*2; // 3a+2}}
}
2. 剑指 Offer 14- II. 剪绳子 II
题目描述:给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m - 1] 。请问 k[0]k[1]…*k[m - 1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
2.1 推导
- 基础推导如1.2.1节所示;
- 此处与上一道题不同的是,n的取值范围变大,因此在求3t时可能会发生边界值溢出的情况;
- 基于取余运算如下图所示的性质,可通过循环取余的方法解决取值范围溢出的问题;

2.2 代码实现
class Solution {public int cuttingRope(int n) {if(n<=2){return 1;}if(n==3){return 2;}int base=1000000007;int res=n/3;int mod=n%3;if(mod==1){res-=1;}// 计算pow(3,res)long target=1;while(res-->0){target=((target%base)*3)%base;}if(mod==0){return (int)(target%base); }else if(mod==1){return (int)((target*4)%base);}else{return (int)((target*2)%base);}}
}