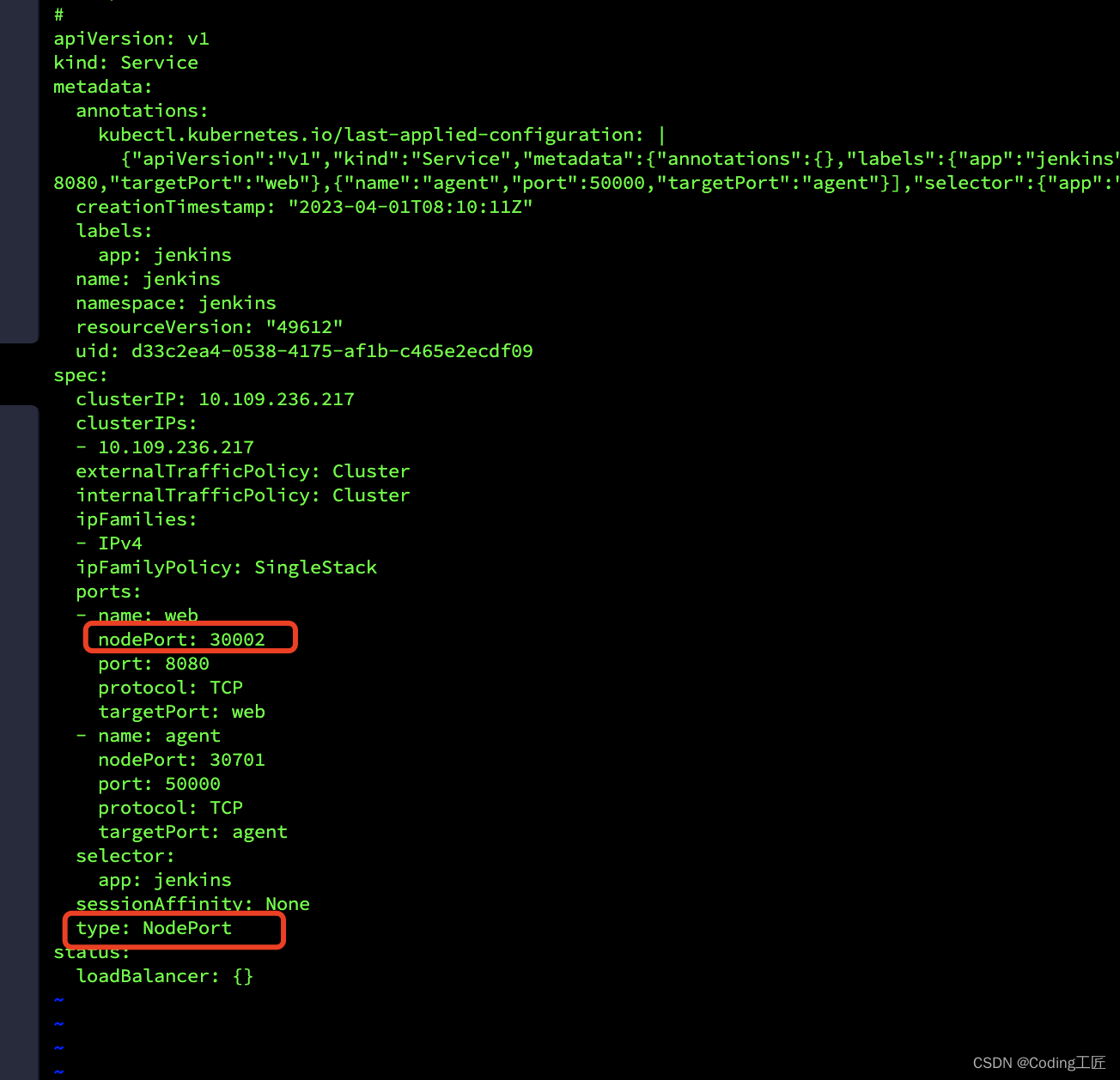
关于量化,之前的博客中首先从第一个将量化思想应用在神经网络模型上的工作开始介绍,随后阐述了量化领域的极端情况,即二值化与三值化,并指出尽管目前已经存在多种对二值网络的优化方法,但是显然因极端量化带来的严重精度损失使得这类量化模型无法满足实际场景中的需求。参考之前博客中的量化分级,本文将主要关注Level3的量化方法,即通过在训练过程中模拟量化,来尽可能地降低由量化带来的精度损失,其属于量化感知训练一类,本小节将介绍的即为量化感知训练方法的一些基础理论。
根据量化间隔是否相等,可将量化方法分为均匀量化与非均匀量化,例如对数量化即为典型的非均匀量化方法,但目前该基于非均匀量化的部署还较难在现有硬件上实现,因此本研究主要关注均匀量化。
在均匀量化中,从量化参数中是否包含零点(Zero Point ,简写为zp )可分为非对称量化与对称量化。为便于理解,下面将通过[67][158]中的量化方案来阐述相关概念,其中非对称量化的计算如式2.6中所示。
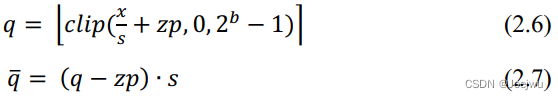
式2.6为量化计算过程,其中的s 为缩放因子,代表量化步长,zp 为零点,代表的是浮点数中的0经量化后的整数值,b 是设置的量化位宽,clip( ) 为截断函数,∙ 代表舍入函数,为传统的向最接近值舍入方式。式2.7中则为反量化过程,用于在量化感知训练过程中来接近原始值。上述两式中涉及到两个量化参数s 与zp ,在量化感知训练过程中,这两个参数的初始化与更新均通过式2.8与式2.9完成。
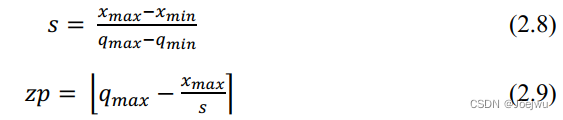
上述两式中,xmax 、xmin 分别表示原浮点值中的最大值与最小值,qmax 则为量化后的最大值。均匀对称量化则是在式2.6与式2.7的基础上删去零点即可,如式2.10与2.11中所示。
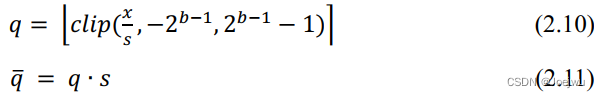
其量化参数s 的初始化与更新则与式2.8中相同。最后从量化粒度的角度,可将量化分为逐通道量化与逐层量化,例如在卷积层中,同一层的每个卷积核(Filter)拥有独立的量化参数则为逐通道量化,若每个卷积核共享同一组量化参数,则为逐层量化。一般来说,量化粒度越细,则量化造成的精度损失越低,但是更细的量化粒度,往往会造成更多的冗余计算,因此需要根据实际的参数分布以及硬件情况来选择量化粒度。
最后来关注一下如何通过量化将原本的浮点运算全部转为定点运算过程。鉴于卷积神经网络的运算本质上是由大量矩阵运算完成,此处不妨以两个矩阵的运算来做实例。首先假设两个大小为N×N 的矩阵r1 与r2 ,r1 与r2 矩阵相乘后得到r3 ,计算如式2.12。

采用最一般的量化方式,即式2.6中的非对称量化,不妨假设r1 矩阵的量化参数分别为s1 与zp1 ,r2 与r3 的量化参数同理设置,可得式2.7。
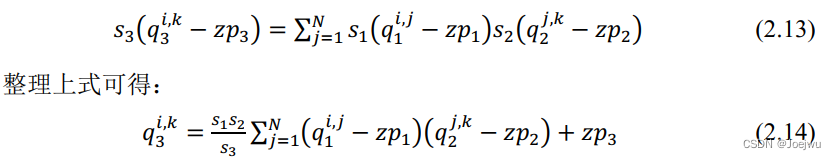
观察式2.14不难发现,除了s1s2/s3 为浮点数,其他运算均为定点数运算,因此此时只需将s1s2/s3 转为定点运算即可。参考[67]中的解决方法,不妨假设M=s1s2/s3 ,通过大量的实验发现,M 的值域通常为(0,1) ,鉴于此,可将其表示为M=2-nM0 ,其中的M0 值域为[0.5,1) ,n转为非负整数。此时,M0 可根据硬件情况表示为一个INT16或INT32的定点乘数,此处不妨假设为INT32,则表示M0 的整数此时是最接近2^31*M0 的INT32整型值,同时由于M0>0.5 ,所以这个值至少为2^30 ,即表明其至少有30位的相对精度,综上,与M0 的乘法运算可通过定点数乘法来完成,而2^-n 则可通过简单的移位来完成。同时鉴于s1s2/s3 中涉及到的量化参数在量化完成后均已知,所以可提前完成s1s2/s3 的近似转换。