本文很多直接截图论文的,因为不需要重复造轮子,对比也只是为了选择更佳的路径规划曲线,对比于B曲线,时间不够,概括会有所疏漏,下表是曲线的对比表格,看完可以直接看下面,也涉及到不同曲线加速度的一些东西,不过有待细化,2022/3/17后来上了高等工程数学,如果有需要建议去高等工程数学的曲面造型部分自己学习。
| 曲线类型 | 性质 | 评价(仅仅针对个人项目而言) |
|---|---|---|
| 贝塞尔曲线 | 1.计算量较大 2. Bezier曲线/曲面不支持局部的修改和编辑 3. Bezier曲线/曲面拼接时,满足几何连续条件是十分困难的 | |
| PH曲线 | 1.具有良好的几何计算优势 2.具有保凸性且无法灵活的处理拐点 | |
| 多项式曲线 | 创新性太低,不讨论 | |
| C曲线 | 1.参数α的引入增强了曲线的控制能力,使曲线具有更灵活的调节性 2.C曲线能够统一表示自由 曲线、圆锥曲线和超越曲线。 | 基本不可用 |
| C-Bézier(C曲线的一个) | 1.在端点处,该曲线具有贝塞尔基类似的性质 2.正性 3.规范性 4.对称性 曲线:凸包性质 | |
| C-B样条曲线(C曲线的另一个) | 1.具有局部性,曲线形状修正较快 2.C-B样条曲线与均匀B样条基函数的图形类似 3. a增加,曲线变得扁平,趋于0曲线变凸 4.增加了表达二次曲线曲面的能力(具有很多B样条曲线的特性) | |
| B样条 | 1. 非负性 2. 局部支撑性 3. 单位分解(所有非零的基函数在区间[ui, ui+1)上的和(sum)是 1) 4.基函数 Ni,p(u) 是p 次多项式的复合曲线,连接点在[ui, ui+p+1 ) 上的节点处 | |
| NURBS样条曲线 | 1.局部支撑性质 2.规范性 3. 可微分性 4.曲线具有局部性质 5. 曲线有变差减少性质与B样条曲线类似 6.曲线有凸包性质 7.曲线具有参数可微性质 | 1,研究成熟 |
| 三次Cardinal样条曲线 | 1.C1连续性 2.形状可调性 3.固定性 4.局部性 5.对称性 6.形状的灵活性 | 2.可以考虑 |
文章目录
- 贝塞尔曲线
- PH曲线
- F曲线
- C曲线
- C-Bézier曲线
- C-B样条
- B样条
- NURBS样条曲线
- 三次Cardinal样条曲线
- 加减速算法
- 直线加减速控制算法
- 指数型加减速控制算法
- 多项式加减速控制算法
- S型曲线加减速算法模型
贝塞尔曲线
贝塞尔曲线于1962年,由法国工程师皮埃尔·贝兹(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由保尔·德·卡斯特里奥于1959年运用德卡斯特里奥算法开发,以稳定数值的方法求出贝塞尔曲线。贝塞尔曲线是一种以伯恩斯坦多项式为基础的样条曲线,n阶层贝塞尔曲线由n+1个线性无关的伯恩斯坦项组成,并由n+1个控制点控制
基本表达式如下图所示:
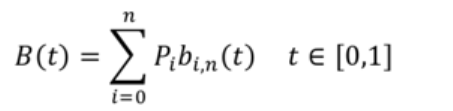

上俩图,摘自华中科技大学毕业论文([1]王达. 基于分段贝塞尔曲线与遗传算法的翼型优化研究[D].华中科技大学,2020.DOI:10.27157/d.cnki.ghzku.2020.002524.)
[伯恩斯坦多项式(Bernstein Polynomials)参考]((9条消息) 伯恩斯坦多项式(Bernstein Polynomials)_Feyily的博客-CSDN博客_伯恩斯坦多项式)
由于高次贝塞尔曲线不可避免地带来计算量的增加,下图列举了1-3次贝塞尔曲线的图片

摘自百科,贝塞尔曲线的公式和定义
Bezier曲线/曲面不支持局部的修改和编辑;
Bezier曲线/曲面拼接时,满足几何连续条件是十分困难的。
PH曲线
如下图定义的曲线则称为PH曲线.这种特殊的代数结构使得PH曲线具备了良好的几何计算优势,如弧长可表示为多项式形式,曲率、等距曲线是有理形式的,于是可被精确计算.因此,PH曲线被广泛应用于计算机辅助设计、机器人技术、运动控制等各种场景中

性质:由于H次PH曲线具有保凸性且无法灵活处理拐点,导致工业设计中常用的PH曲线最低次数大多为五次,但次数很高,在运动规划中用处不大,且拐点也存在大问题

依旧列举五次曲线的性质

F曲线


C曲线
C—曲线是在多项式幂基的基础上引入三角函数的一类特殊代数曲线.为了克服多项式参数曲线无法精确地表示圆、椭圆、摆线等的问题,

李毓君等论文
C曲线是Bézier曲线和B样条曲线的一种推广,C-Bézier曲线和C-B样条曲线统称为C曲线.它们都含有形状参数α,参数α的引入增强了曲线的控制能力,使曲线具有更灵活的调节性,C曲线能够统一表示自由 曲线、圆锥曲线和超越曲线。
C-Bézier曲线
来自以下论文的整理内容
[1]杭颖. C曲线及其形状修改[D].合肥工业大学,2009.

其基函数具有的性质

曲线的性质



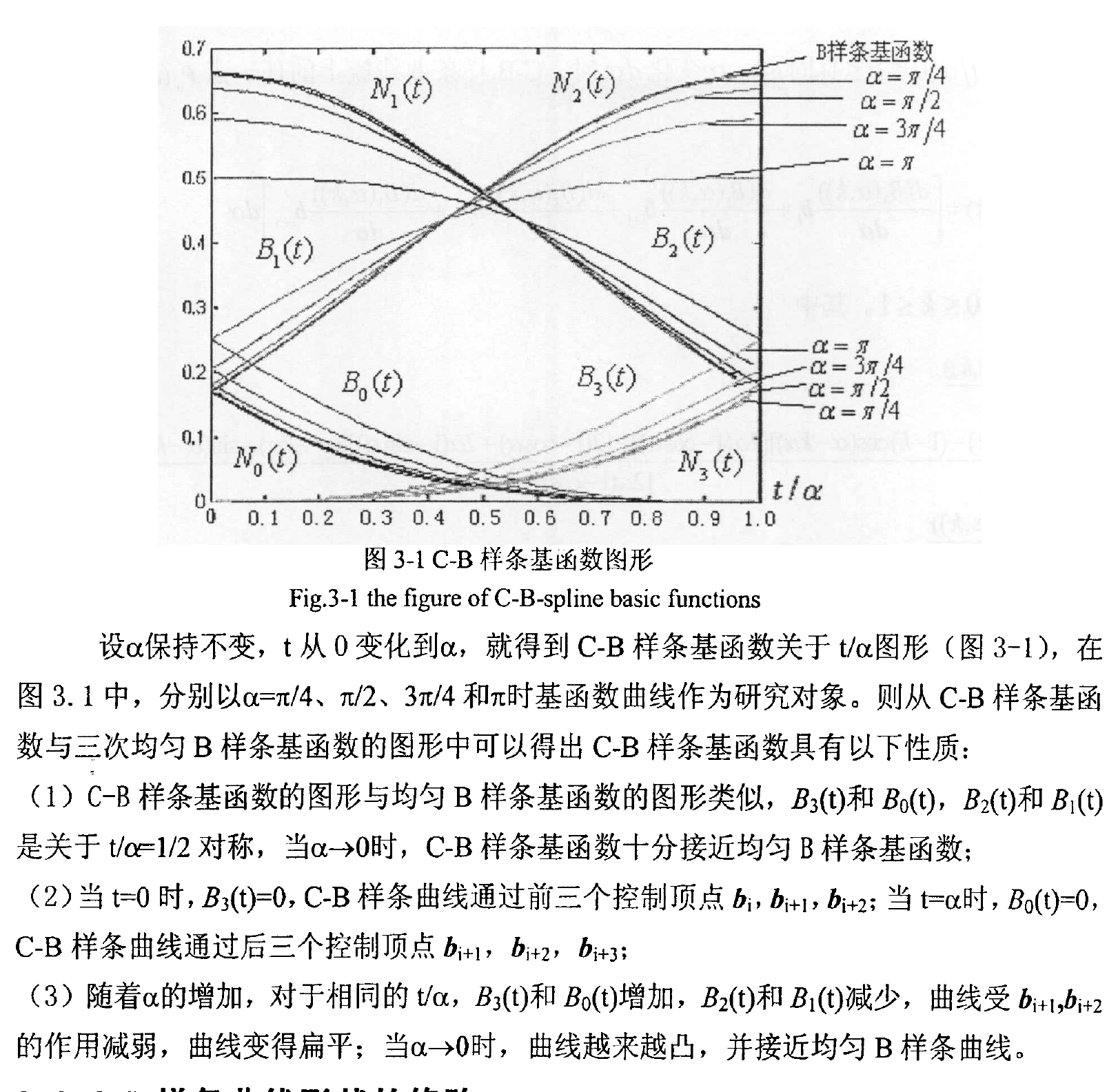
C-B样条
一样条曲线属于一曲线中的一种,一方面具有许多样条曲线的特性,另一方面
又能精确地表示圆弧和椭圆弧等二次曲线弧。由于工程曲线或曲面的轮廓线及截面线包含有二次曲线弧的情况比比皆是




B样条
可以参考下面的两个链接
深入理解B样条曲线(上) - 知乎 (zhihu.com)
B样条曲线(B-spline Curves)_余生最年轻的博客-CSDN博客_b样条曲线
B样条曲线按其节点矢量中节点的分布情况,可划分为四种类型:(其余的参考上文)
-
均匀B样条曲线
节点矢量中节点为沿参数轴均匀或等距分布,所有节点区间长度为常数。这样的节点矢量定义了均匀的B样条基。 -
准均匀B样条曲线
与均匀B样条曲线的差别在于两端节点具有重复度k,这样的节点矢量定义了准均匀的B样条基。均匀B样条曲线没有保留Bézier曲线端点的几何性质,即样条曲线的首末端点不再是控制多边形的首末端点。采用准均匀的B样条曲线解决了这个问题 -
分段Bézier曲线
节点矢量中两端节点具有重复度k,所有内节点重复度为k-1,这样的节点矢量定义了分段的Bernstein基。
B样条曲线用分段Bézier曲线表示后,各曲线段就具有了相对的独立性,移动曲线段内的一个控制顶点只影响该曲线段的形状,对其它曲线段的形状没有影响。并且Bézier曲线一整套简单有效的算法都可以原封不动地采用。缺点是增加了定义曲线的数据,控制顶点数及节点数。 -
非均匀B样条曲线
任意分布的节点矢量,只要在数学上成立(节点序列非递减,两端节点重复度≤k,内节点重复度≤k-1)都可选取。这样的节点矢量定义了非均匀B样条基
(原文链接:https://blog.csdn.net/mofadiyu/article/details/107738411 也可以参考 计算机辅助几何设计与非均匀有理B样条 )
NURBS样条曲线








三次Cardinal样条曲线
Cardinal样条曲线是插值分段三次曲线,相比较更高次的多项式样条曲线, 其计算更加简便快捷,所占用的空间也较少,能有效提高加工效率,而更低次的 多项式虽然计算更简单,但是精度较低,而且曲线形状较为单一。不重复造轮子,参考最后的参考文献



形状可调性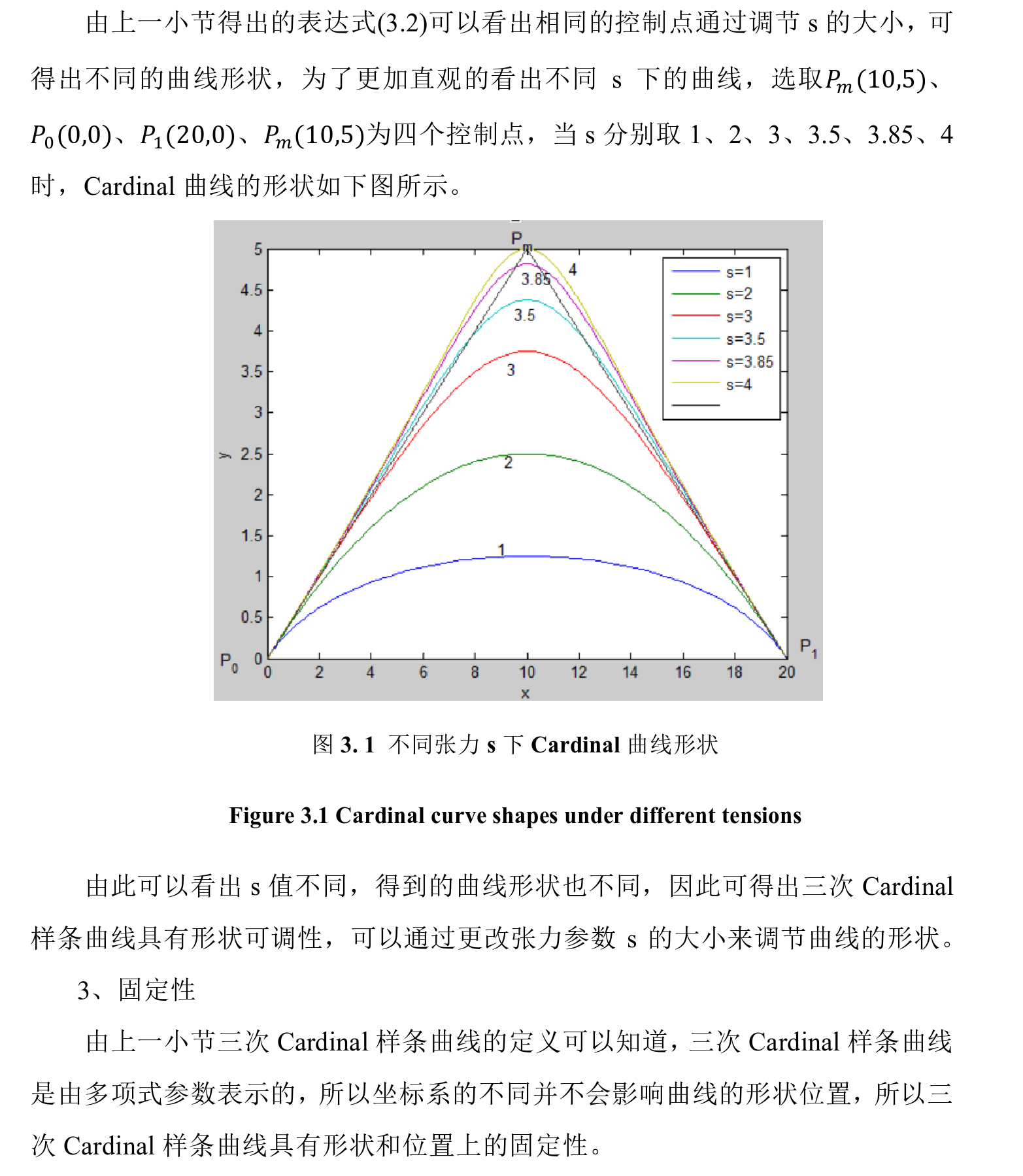










加减速算法
直线加减速控制算法
直线加减速的原理比较简单,以固定常数的加速度控制速度变化,具体的加 减速过程大致如下:加速阶段,按照恒定的加速度匀加速到机床所允许的最大加 工速度;匀速阶段,保持最大速度不变匀速运行;减速阶段,按恒定的减加速度 减速至终点位置。直线加减速是传统加减速控制算法中最简单的、最常用的,虽 然它能够保证速度的连续性,但是却存在加速度上的突变,因此在高精高速加工 过程中加工质量较低。
优缺点:存在加速度突变情况,计算简单
指数型加减速控制算法
指数型加减速相比较直线加减速,平滑性更好,有更好的稳定性。指数型加 减速控制算法的基本原理是在加速阶段和减速阶段速度都是按照指数形式变化, 共包括三个阶段:加速阶段、匀速阶段、减速阶段。虽然它比直线加减速的平滑 性更好,能够保证速度柔性变化,但是指数型加减速控制算法较复杂,占用时长 较长,速度较慢,并且只解决了部分加速度突变,在起始点以及开始减速点仍然 存在加速度的突变。
优缺点:存在加速度上 的突变,总体柔性依旧较差
多项式加减速控制算法
多项式加减速控制算法从根本上解决了加速度突变的问题,多项式加减速 控制算法能够保证加速度连续,整个加减速控制阶段没有出现加速度的突变,能 够保证加工过程的平稳进行,但计算复杂。
优缺点:存在加速度上 的突变,总体柔性依旧较差,加速度不恒定
S型曲线加减速算法模型

优缺点:存在加速度上 的突变,总体柔性依旧较差,加减速加速度恒定
[1]李毓君,方林聪.Pythagorean-Hodograph C-曲线的几何构造方法[J/OL].数学学报(中文版):1-12[2022-11-07].http://kns.cnki.net/kcms/detail/11.2038.O1.20220422.1420.004.html]
[2]宋九锡. 带参数的PH曲线构造及其应用研究[D].辽宁师范大学,2022.DOI:10.27212/d.cnki.glnsu.2022.001126.
[3]丁晨. PH曲线的若干问题及应用研究[D].合肥工业大学,2015.
[4]孙璐璐. 关于PH曲线插值若干问题的研究[D].合肥工业大学,2010.
[5]袁家兰. 基于Cardinal样条曲线的微小线段间平滑过渡算法的设计与实现[D].中国科学院大学(中国科学院沈阳计算技术研究所),2018.
[6]林新辉. C-Bézier曲线降阶逼近[D].浙江大学,2007.
[7]宋丽平. C-B样条曲线曲面理论及其在造型中的应用[D].西安理工大学,2008.






