一、关于图的几个概念定义：

连通图：在无向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该无向图为连通图。
强连通图：在有向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该有向图为强连通图。
连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

二、最小生成树基础知识：

1、定义：

最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。简单说就是在一个连通图上创建一棵树，使这棵树能遍历所以结点，且路径值最小，且树不能有环，这样的树叫最小生成树。

2、特点：

没有环
任意2个顶点都是互通的
n顶点，n-1条边

3、示例：

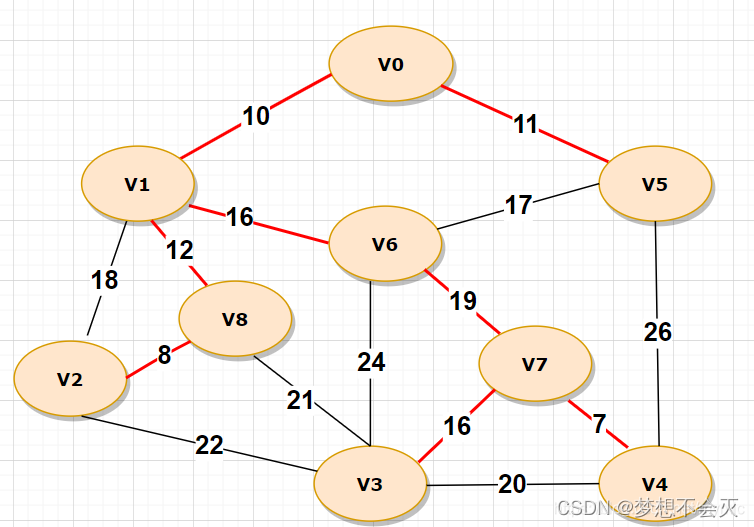
有连通图如下：
在这里插入图片描述
生成的最小生成树就下图中的红色边：

4、最小生成树使用场景

最小生成树一般可用于求解最短路径问题，场景有城市、网络等。连通图中连接所有点且权值最小。

三、最小生成树算法

通常来说，要解决最小生成树问题，通常采用两种算法：Prim算法和Kruskal算法

1、Prim(普里姆)算法

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

具体步骤如下：

图的所有顶点集合为V；初始令集合u={s},v=V−u;
在两个集合u,v能够组成的边中，选择一条代价最小的边(u0,v0)，加入到最小生成树中，并把v0并入到集合u中。
重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

假设起点为A
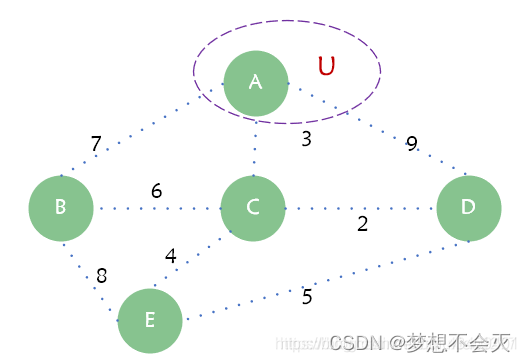
在这里插入图片描述
其它剩余点到集合u的最小边，A->C，C加入u集合

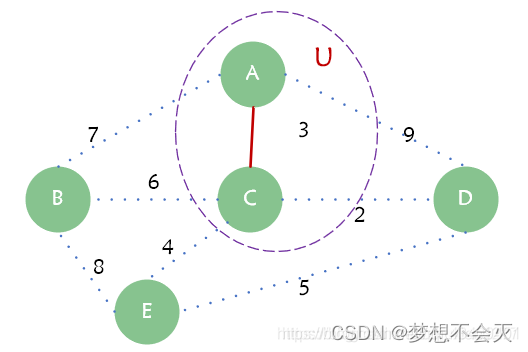
其它剩余点到集合u的最小边，C->D，D加入u集合

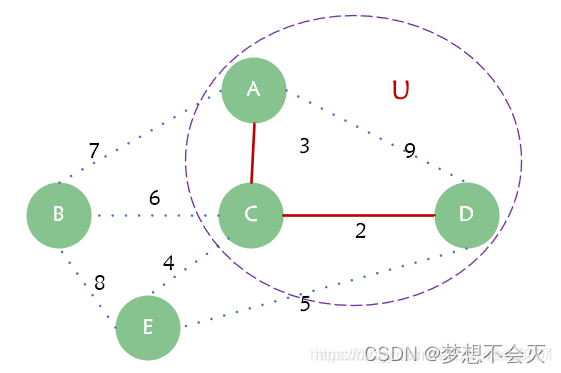
在这里插入图片描述
由此类推，得出最小生成树

2、Kruskal(克鲁斯卡尔)算法

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

具体步骤如下：

把图中的所有边按代价从小到大排序；
把图中的n个顶点看成独立的n棵树组成的森林；
按权值从小到大选择边，若形成环，不选，所选的边连接的两个顶点ui,vi，应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。
重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

四、代码实现

代码采用的算法思想是Kruskal算法

1、图的边类

public class Edge {/*** 连接该条边的一个结点*/private EdgeNode edgeNode1;/*** 连接该条边的另一个结点*/private EdgeNode edgeNode2;/*** 该边的权值*/private int weight;public Edge(EdgeNode edgeNode1, EdgeNode edgeNode2, int weight) {this.edgeNode1 = edgeNode1;this.edgeNode2 = edgeNode2;this.weight = weight;}public EdgeNode getEdgeNode1() {return edgeNode1;}public void setEdgeNode1(EdgeNode edgeNode1) {this.edgeNode1 = edgeNode1;}public EdgeNode getEdgeNode2() {return edgeNode2;}public void setEdgeNode2(EdgeNode edgeNode2) {this.edgeNode2 = edgeNode2;}public int getWeight() {return weight;}public void setWeight(int weight) {this.weight = weight;}
}

2、节点类

public class EdgeNode {/*** 节点名称*/private String nodeName;public String getNodeName() {return nodeName;}public void setNodeName(String nodeName) {this.nodeName = nodeName;}public EdgeNode(String nodeName) {this.nodeName = nodeName;}
}

3、具体算法类

public class Solution {private   ArrayList<Edge> list=new ArrayList<>();private   HashMap<String,EdgeNode> nodeMap=new HashMap<>();/*** 构件图* @param node1* @param node2* @param weight*/public void createMGraph(String node1,String node2,int weight){EdgeNode edgeNode1 = nodeMap.get(node1);EdgeNode edgeNode2 = nodeMap.get(node2);// 如果点不存在,则新构建一个点,如果存在就使用存在的点if (edgeNode1==null) {edgeNode1 = new EdgeNode(node1);nodeMap.put(node1,edgeNode1);}if (edgeNode2==null){edgeNode2 = new EdgeNode(node2);nodeMap.put(node2,edgeNode2);}list.add(new Edge(edgeNode1,edgeNode2,weight));}public void miniTree(){String nodeName1, nodeName2;// 用于存放最小生成树的边Map<String,String> map =new HashMap<>();// 将图中的所有边按权重从小到大排序list.sort(Comparator.comparingInt(Edge::getWeight));for (int i = 0,j=1; i <list.size() ; i++) {nodeName1=find(map,list.get(i).getEdgeNode1().getNodeName());nodeName2=find(map,list.get(i).getEdgeNode2().getNodeName());if (!nodeName1.equals(nodeName2)){// 两个点不相等,记录这一条边map.put(nodeName1,nodeName2);// 得到路径System.out.println("路径"+j++ +":"+"开始结点："+list.get(i).getEdgeNode1().getNodeName()+";结束结点："+list.get(i).getEdgeNode2().getNodeName()+";权值："+list.get(i).getWeight());}}}/*** 该方法用于判断两个结点连接后是否会形成环* @param map 已经遍历过的节点集合* @param nodeName 将要遍历的节点名称* @return*/private String find(Map<String ,String > map,String nodeName){// 循环找到没有遍历过的点while (map.get(nodeName)!=null){nodeName=map.get(nodeName);}return nodeName;}
}

4、测试类

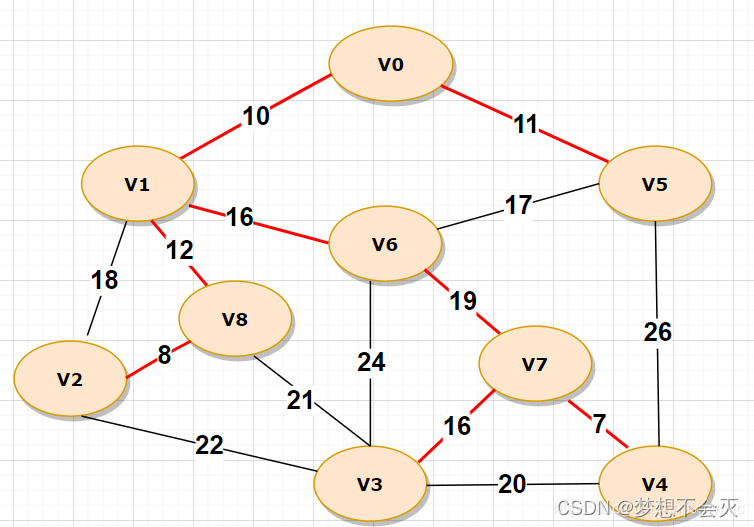
构建如下的图
在这里插入图片描述

public class Test {public static void main(String[] args) {Solution t=new Solution();//构造以上的例图t.createMGraph("V0","V1",10);t.createMGraph("V0","V5",11);t.createMGraph("V1","V2",18);t.createMGraph("V1","V8",12);t.createMGraph("V1","V6",16);t.createMGraph("V2","V8",8);t.createMGraph("V2","V3",22);t.createMGraph("V3","V8",21);t.createMGraph("V3","V6",24);t.createMGraph("V3","V7",16);t.createMGraph("V3","V4",20);t.createMGraph("V4","V7",7);t.createMGraph("V4","V5",26);t.createMGraph("V5","V6",17);t.createMGraph("V6","V7",19);t.miniTree();}
}

5、结果

路径1:开始结点：V4;结束结点：V7;权值：7
路径2:开始结点：V2;结束结点：V8;权值：8
路径3:开始结点：V0;结束结点：V1;权值：10
路径4:开始结点：V0;结束结点：V5;权值：11
路径5:开始结点：V1;结束结点：V8;权值：12
路径6:开始结点：V1;结束结点：V6;权值：16
路径7:开始结点：V3;结束结点：V7;权值：16
路径8:开始结点：V6;结束结点：V7;权值：19

即生成的最小生成树为
在这里插入图片描述

五、场景案例题目实战

1、题目

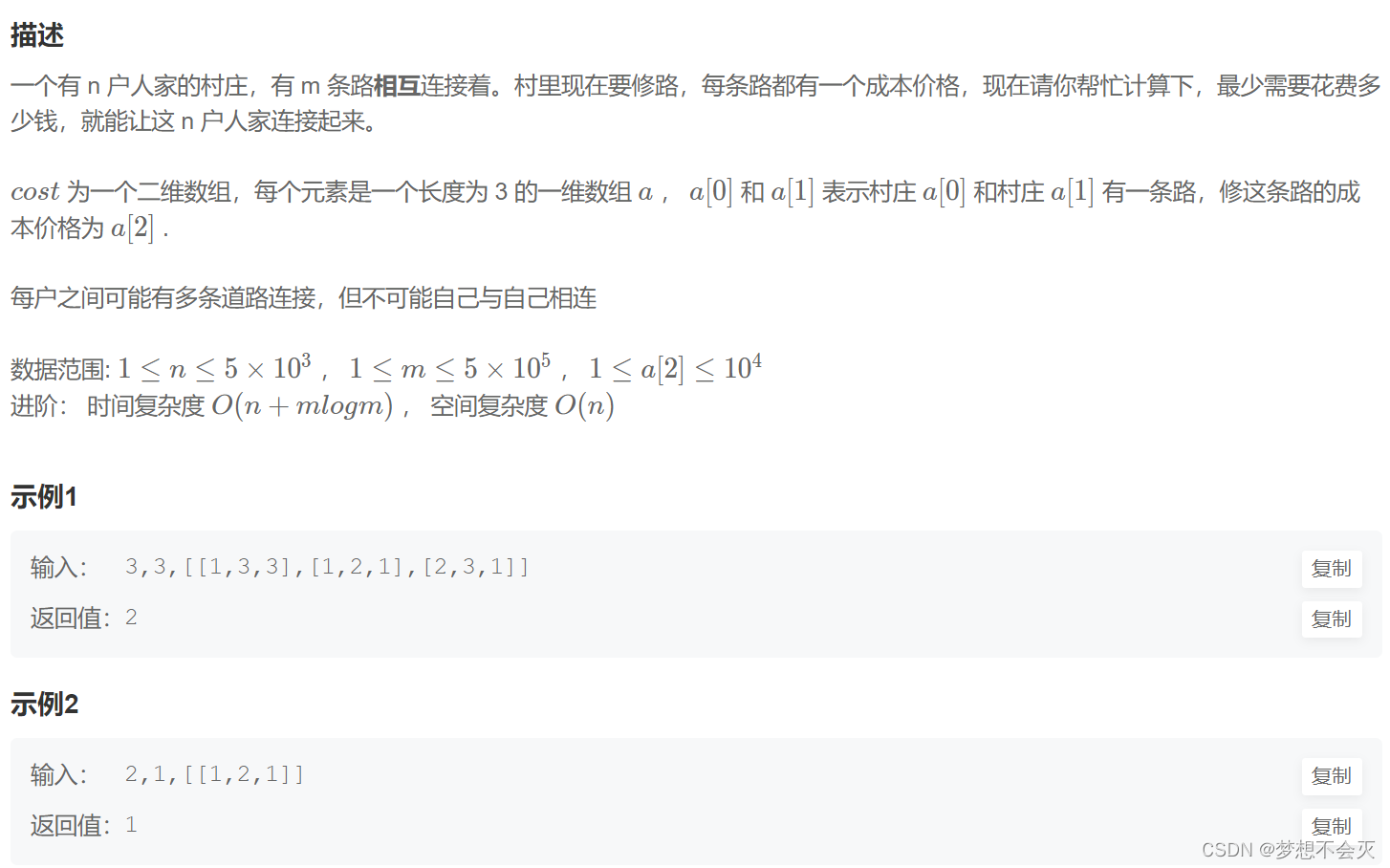
在这里插入图片描述

2、代码

import java.util.*;public class Solution {/*** 存图的边*/private static ArrayList<Edge> list = new ArrayList<>();/*** 存图的节点*/private static HashMap<Integer, EdgeNode> nodeMap = new HashMap<>();/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** 返回最小的花费代价使得这n户人家连接起来* @param n int n户人家的村庄* @param m int m条路* @param cost int二维数组 一维3个参数，表示连接1个村庄到另外1个村庄的花费的代价* @return int*/public int miniSpanningTree (int n, int m, int[][] cost) {// write code hereSolution t = new Solution();for (int i = 0; i < cost.length; i++) {int[] edge = cost[i];t.createGraph(edge[0],edge[1],edge[2]);}return getMiniTree();}/*** 构件图* @param node1* @param node2* @param weight*/public void createGraph(int node1, int node2, int weight) {// 如果点不存在,则新构建一个点,如果存在就使用存在的点EdgeNode edgeNode1 = nodeMap.get(node1);EdgeNode edgeNode2 = nodeMap.get(node2);if(edgeNode1 == null){edgeNode1 = new EdgeNode(node1);nodeMap.put(node1,edgeNode1);}if(edgeNode2 == null){edgeNode2 = new EdgeNode(node2);nodeMap.put(node2,edgeNode2);}Edge edge = new Edge(edgeNode1,edgeNode2,weight);list.add(edge);}public Integer getMiniTree() {// 将图中的所有边按权重从小到大排序list.sort(Comparator.comparingInt(Edge::getWeight));Map<Integer,Integer> nodeMap = new HashMap<>(16);int result = 0;Integer nodeName1,nodeName2;for (int i = 0,j = 1; i < list.size(); i++) {nodeName1 = find(nodeMap,list.get(i).getEdgeNode1().getNodeName());nodeName2 = find(nodeMap,list.get(i).getEdgeNode2().getNodeName());if(!nodeName1.equals(nodeName2)){// 两个点不相等,记录这一条边nodeMap.put(nodeName1,nodeName2);result += list.get(i).getWeight();}}return result;}/*** 该方法用于判断两个结点连接后是否会形成环* @param map 已经遍历过的节点集合* @param nodeName 将要遍历的节点名称* @return*/private Integer find(Map<Integer, Integer> map, Integer nodeName) {// 循环直到没有遍历过的点while(map.get(nodeName) != null){nodeName = map.get(nodeName);}return nodeName;}
}class Edge {private EdgeNode edgeNode1;private EdgeNode edgeNode2;private int weight;public Edge(EdgeNode edgeNode1, EdgeNode edgeNode2, int weight) {this.edgeNode1 = edgeNode1;this.edgeNode2 = edgeNode2;this.weight = weight;}public EdgeNode getEdgeNode1() {return edgeNode1;}public void setEdgeNode1(EdgeNode edgeNode1) {this.edgeNode1 = edgeNode1;}public EdgeNode getEdgeNode2() {return edgeNode2;}public void setEdgeNode2(EdgeNode edgeNode2) {this.edgeNode2 = edgeNode2;}public int getWeight() {return weight;}public void setWeight(int weight) {this.weight = weight;}
}class EdgeNode {private Integer nodeName;public Integer getNodeName() {return nodeName;}public void setNodeName(Integer nodeName) {this.nodeName = nodeName;}public EdgeNode(Integer nodeName) {this.nodeName = nodeName;}
}