这里写目录标题
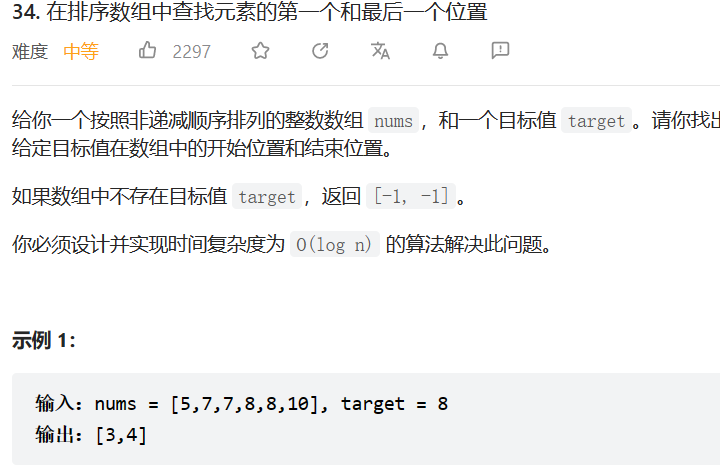
- 34. 在排序数组中查找元素的第一个和最后一个位置
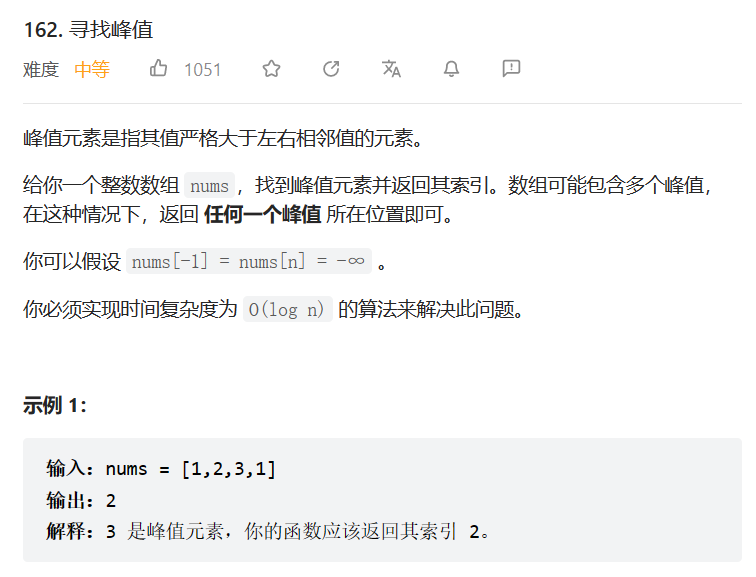
- 162. 寻找峰值
- 153. 寻找旋转排序数组中的最小值
- 33. 搜索旋转排序数组
34. 在排序数组中查找元素的第一个和最后一个位置
题目链接
vector<int> searchRange(vector<int>& nums, int target) {int left=0,right=nums.size()-1;vector<int> ret{-1,-1};while(left<=right)//区间不为空,则可以继续去找{int mid=(left+right)/2;//int mid=left+(right-left)/2;这样写不会越界,如果left和right都很大,相加就可能越界if(nums[mid]==target){int i;for(i=mid-1;i>=0&&nums[i]>=target;i--)/*找到target不能立即存放到ret中,因为题目要求找到第一个和最后一个target位置,先从mid往前找,相同 就给ret[0]赋当前下标,对mid右变处理相同因为是有序的,所以加上nums[i]>=target,往前找,不过遇到大于target则前面不可能再有了*/if(nums[i]==target)ret[0]=i;if(ret[0]==-1)ret[0]=mid;for(i=mid+1;i<nums.size()&&nums[i]<=target;i++)if(nums[i]==target)ret[1]=i;if(ret[1]==-1)ret[1]=mid;}if(nums[mid]<target)left=mid+1;else right=mid-1;}return ret;
似乎这样写没有问题,并且也通过了测试用例,但是仔细分析就会发现,在某些特定数组的情况
比如:target=2 序列是:1 22222222222222222222222222222222…2222 1
中间有很多很多2,那么这个算法的效率就不是O(logn)了,接近O(n)
正确写法:
那么问题出在哪里,因为我们的二分是对小于(mid<target)进行mid+1,大于进行mid-1,相等就往前找,和往后找,这里简单理解为return而应该在相等时也不return,相等应该归类于大于的情况,说明前面还可能有,继续找这时就可以理解为right指针不断向前,并且是跳跃式向前找,target,最后left的位置就是第一个target的位置,为什么是left而不是right,因为right不断向前最中总能找到一个不等的或者区间为空了1.不等情况:此时right指向的不等于target,那么肯定是mid小于了,left指针此时向后移动,如此循环直到区间只剩一个元素,则该元素就是第一个target2.区间为空:则不存在这样的元素,那么此时left和right的情况是怎样的?区间为空说明mid一次都没有匹配target,则left一直后移,最终left指向right+1,全过程right都没有变化区间为空还有一种情况是数组中没有target,但是两遍是符合的,也就是left和right都会移动
inline int lower_bound(vector<int>& nums,int target){int left=0,right=nums.size()-1;while(left<=right){int mid=left+(right-left)/2;if(nums[mid]<target)left=mid+1;else right=mid-1;//为什么没有相等,以及下面为什么返回left,都在上面解释过了}return left;}vector<int> searchRange(vector<int>& nums, int target) {int start=lower_bound(nums,target);if(start==nums.size()||nums[start]!=target)//区间为空有两种情况return {-1,-1};int end=lower_bound(nums,target+1)-1;//end要找target+1,最后在-1找前一个return {start,end};}
};
返回值为vector<int>为什么可以返回return {start,end};
因为 vector<int> arr{ 1, 1};可以用初始化列表初始化容器vector
感觉第二种不好理解啊,low_bound还行,但是在searchRange中比较复杂,还是第一种的思路简单,有没有什么办法优化第一种呢?
方法一的问题在于,遇到特殊相等之后就不在是二分算法了,那么应该当相等时,继续二分,更新边界,那边界应该如何去选择呢,这就要看是要找第一个target还是第二个target,对于ret[0],则要更新right=mid+1
对于ret[1],更新left=mid-1,分两次二分就可以解决
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {return {searchLeftOrRightBound(nums, target, "left"), searchLeftOrRightBound(nums, target, "right")};}
private:int searchLeftOrRightBound(vector<int>& nums, int target, const string& bound) {int left = 0, right = nums.size() - 1;int res = -1;while (left <= right) {int mid = (left + right) >> 1;if (nums[mid] < target) {left = mid + 1;}else if (nums[mid] > target) {right = mid - 1;}else {res = mid;if (bound == "left") {right = mid - 1;}else if (bound == "right") {left = mid + 1;}}}return res;}
};
162. 寻找峰值
题目链接
class Solution {
public:
/*这道题,最最最重要的是条件,条件,条件,两边都是负无穷,数组当中可能有很多波峰,也可能只有一个,如果尝试画图,就跟股票信息一样,没有规律,如果根据中点値判断我们的二分方向该往何处取, 这道题还有只是返回一个波峰。你这样想,中点所在地方,可能是某座山的山峰,山的下坡处,山的上坡处,如果是山峰,最后会二分终止也会找到,关键是我们的二分方向,并不知道山峰在我们左边还是右边,送你两个字你就明白了,爬山(没错,就是带你去爬山),如果你往下坡方向走,也许可能遇到新的山峰,但是也许是一个一直下降的坡,最后到边界。但是如果你往上坡方向走,就算最后一直上的边界,由于最边界是负无穷,所以就一定能找到山峰,总的一句话,往递增的方向上,二分,一定能找到,往递减的方向只是可能找到,也许没有。*/
//二分的过程就是模拟爬山,寻找波峰int findPeakElement(vector<int>& nums) {int left=0,right=nums.size()-1;while(left<right){int mid=(left+right)/2;if(nums[mid]<nums[mid+1])//左侧小于右侧,说明是在爬坡,并且题目说nums[n] = -ooleft=mid+1;else right=mid;//不能是mid-1,因为mid也有可能是个波峰}return left;}
};
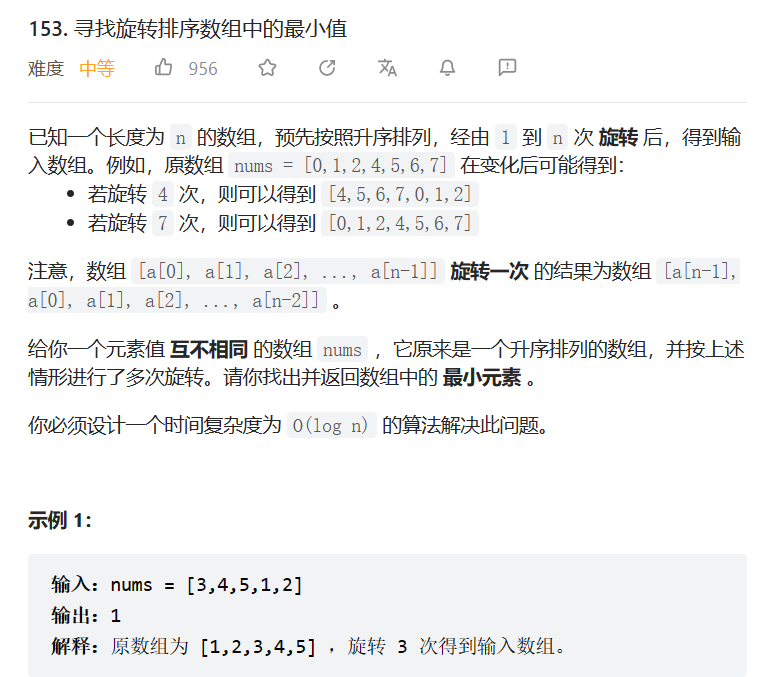
153. 寻找旋转排序数组中的最小值
题目链接
class Solution {public:/*根据题意可以知道:该序列有两段上坡,可以视为一段高坡,一段低坡并且对于末尾元素x,最小值右侧都大于x,最小值左侧都小于x*/int findMin(vector<int> & nums) {int left = 0, right = nums.size() - 1;while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] < nums[nums.size() - 1]) //和末尾元素比较。mid小于末尾,说明在低坡。最小值一定在mid左侧,并且mid的位置有可能就是最小值位置,所以是right=mid(这是因为最小值一定在小坡上,小坡坡底)right = mid;else //mid 大于末尾,说明在一定在大坡,大坡是不可能有最小值的,直接mid+1left = mid + 1;}return nums[left];}
};
33. 搜索旋转排序数组

题目链接
思路
先找到要二分的区间位置,有两个坡,那就先找最小值位置,通过比较target和最小值,来判断在哪个坡
class Solution {public:int search(vector<int> & nums, int target) {int left = 0, right = nums.size() - 1;bool asc = true;//升序标记if (nums[left] > nums[right])asc = false;if (asc == false) {//逆序,说明进行了旋转,有两个坡,先找坡底最小值if (target < nums[left] && target > nums[right])return -1;while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] < nums[nums.size() - 1])right = mid;else left = mid + 1;}if (target < nums[0])right = nums.size() - 1;else left = 0;cout << "left=" << left << " " << right << endl;}//确定好在哪个坡了,标准二分while (left <= right) {int mid = (left + right) / 2;if (nums[mid] == target)return mid;else if (nums[mid] < target)left = mid + 1;else right = mid - 1;}return -1;}
};