分析A/B测试结果
目录
- 简介
- I - 概率
- II - A/B 测试
- III - 回归
简介
为了得出电子商务网站运行的 A/B 测试的结果,帮助公司弄清楚是否应该使用新的页面,保留旧的页面,或者应该将测试时间延长,之后再做出决定。
I - 概率
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as plt
%matplotlib inlinerandom.seed(42)
a. 导入数据集,并在这里查看前几行。
df = pd.read_csv('ab_data.csv')
df.head()
| user_id | timestamp | group | landing_page | converted | |
|---|---|---|---|---|---|
| 0 | 851104 | 2017-01-21 22:11:48.556739 | control | old_page | 0 |
| 1 | 804228 | 2017-01-12 08:01:45.159739 | control | old_page | 0 |
| 2 | 661590 | 2017-01-11 16:55:06.154213 | treatment | new_page | 0 |
| 3 | 853541 | 2017-01-08 18:28:03.143765 | treatment | new_page | 0 |
| 4 | 864975 | 2017-01-21 01:52:26.210827 | control | old_page | 1 |
b. 探索数据集。
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 294478 entries, 0 to 294477
Data columns (total 5 columns):
user_id 294478 non-null int64
timestamp 294478 non-null object
group 294478 non-null object
landing_page 294478 non-null object
converted 294478 non-null int64
dtypes: int64(2), object(3)
memory usage: 11.2+ MB
df.shape
(294478, 5)
c. 数据集中独立用户的数量。
df['user_id'].nunique()
290584
d. 用户转化的比例。
df[df['converted'] == 1].count()[0] / df.count()[0]
0.11965919355605512
e. new_page 与 treatment 不一致的次数。
df[(df['landing_page'] == 'old_page') & (df['group'] == 'treatment')].count()[0]
1965
f. 是否有任何行存在缺失值?
df.isnull().sum()
user_id 0
timestamp 0
group 0
landing_page 0
converted 0
dtype: int64
2. 对于 treatment 不与 new_page 一致的行或 control 不与 old_page 一致的行,我们不能确定该行是否真正接收到了新的或旧的页面。删除不确定是否接收的数据,在分析。
a. 将删除不确定是否接收后的数据存储在 df2 中。
df_nc = df[(df['landing_page'] == 'new_page') & (df['group'] == 'control')]df_ot = df[(df['landing_page'] == 'old_page') & (df['group'] == 'treatment')]df_notclear = pd.concat([df_nc, df_ot])
df2 = df.drop(index=df_notclear.index)
# Double Check all of the correct rows were removed - this should be 0
df2[((df2['group'] == 'treatment') == (df2['landing_page'] == 'new_page')) == False].shape[0]
0
df2.head()
| user_id | timestamp | group | landing_page | converted | |
|---|---|---|---|---|---|
| 0 | 851104 | 2017-01-21 22:11:48.556739 | control | old_page | 0 |
| 1 | 804228 | 2017-01-12 08:01:45.159739 | control | old_page | 0 |
| 2 | 661590 | 2017-01-11 16:55:06.154213 | treatment | new_page | 0 |
| 3 | 853541 | 2017-01-08 18:28:03.143765 | treatment | new_page | 0 |
| 4 | 864975 | 2017-01-21 01:52:26.210827 | control | old_page | 1 |
3. 使用 df2 与下面的单元格来回答课堂中的 测试3 。
a. df2 中有290584唯一的 user_id?
df2["user_id"].nunique()
290584
b. df2 中有一个重复的 773192 的ID
dup_user_id = df2["user_id"][df2["user_id"].duplicated()].get_values()[0]print("df2 中有一个重复的 {} 的ID".format(dup_user_id))
df2 中有一个重复的 773192 的ID
c. 观察这个重复的 user_id 的行信息。
df2[df2["user_id"] == dup_user_id]
| user_id | timestamp | group | landing_page | converted | |
|---|---|---|---|---|---|
| 1899 | 773192 | 2017-01-09 05:37:58.781806 | treatment | new_page | 0 |
| 2893 | 773192 | 2017-01-14 02:55:59.590927 | treatment | new_page | 0 |
d. 删除 一个 含有重复的 user_id 的行, 但需要确保你的 dataframe 为 df2。
df2.drop(index=df2[df2["user_id"] == dup_user_id].index[0], inplace=True)
4.
a. 不管它们收到什么页面,单个用户的转化率是多少?
def tran_nub(data):tran = data[data['converted'] == 1].count()[0] / data.count()[0] return tran
print("任意页面,单个用户的转化率是{:.4f}%。".format(tran_nub(df2)*100))
任意页面,单个用户的转化率是11.9597%。
b. 假定一个用户处于 control 组中的转化率
control_group = df[df['group'] == 'control']print("控制组中,单个用户的转化率是{:.4f}%。".format(tran_nub(control_group)*100));
控制组中,单个用户的转化率是12.0399%。
c. 假定一个用户处于 treatment 组中的转化率
treatment_group = df[df['group'] == 'treatment']print("测试组中,单个用户的转化率是{:.4f}%。".format(tran_nub(treatment_group)*100));
测试组中,单个用户的转化率是11.8920%。
d. 一个用户收到新页面的概率
rec_newpage = (df2['landing_page'] == 'new_page').mean()print("一个用户收到新页面的概率为{:.4f}%。".format(rec_newpage*100))
一个用户收到新页面的概率为50.0062%。
e. 没有证据表明新页面可以带来更多的转化.
II - A/B 测试
由于与每个事件相关的时间戳,进行每次观察时连续运行假设检验。
然而,问题的难点在于,一个页面被认为比另一页页面的效果好得多的时候你就要停止检验吗?还是需要在一定时间内持续发生?你需要将检验运行多长时间来决定哪个页面比另一个页面更好?
1. 现在,根据提供的所有数据做出决定。如果想假定旧的页面效果更好,除非新的页面在类型I错误率为5%的情况下才能证明效果更好,做出零假设和备择假设 p o l d p_{old} pold 与 p n e w p_{new} pnew。
H0: P_new - P_old <= 0
H1: P_new - P_old > 0
2. 假定在零假设中,不管是新页面还是旧页面, p n e w p_{new} pnew and p o l d p_{old} pold 都具有等于 转化 成功率的“真”成功率,也就是说, p n e w p_{new} pnew 与 p o l d p_{old} pold 是相等的。
执行两次页面之间 转化 差异的抽样分布,计算零假设中10000次迭代计算的估计值。
使用下面的单元格提供这个模拟的必要内容。如果现在还没有完整的意义,不要担心,你将通过下面的问题来解决这个问题。你可以通过做课堂中的 测试 5 来确认你掌握了这部分内容。
a. 在零假设中, p n e w p_{new} pnew 的 convert rate(转化率) 是11.9597% 。
P_new = df2['converted'].mean()
print(P_new)
0.11959708724499628
b. 在零假设中, p o l d p_{old} pold 的 convert rate(转化率) 是是11.9597%
P_old = P_new
print(P_old)
0.11959708724499628
c. n n e w n_{new} nnew 是多少?
n_new = df2[(df2['landing_page']=='new_page')].count()[0]
print(n_new)
145310
d. n o l d n_{old} nold?是多少?
n_old = df2[(df2['landing_page']=='old_page')].count()[0]
print(n_old)
145274
e. 在零假设中,使用 p n e w p_{new} pnew 转化率模拟 n n e w n_{new} nnew 交易,并将这些 n n e w n_{new} nnew 1’s 与 0’s 存储在 new_page_converted 中。(提示:可以使用 numpy.random.choice。)
new_page_converted = np.random.choice([0,1],size=n_new,p=[(1-P_new), P_new])
print(new_page_converted)
[0 0 0 ... 0 0 0]
f. 在零假设中,使用 p o l d p_{old} pold 转化率模拟 n o l d n_{old} nold 交易,并将这些 n o l d n_{old} nold 1’s 与 0’s 存储在 old_page_converted 中。
old_page_converted = np.random.choice([0,1],size=n_old,p=[(1-P_old), P_old])
print(old_page_converted)
[0 0 0 ... 0 0 0]
g. 在 (e) 与 (f)中找到 p n e w p_{new} pnew - p o l d p_{old} pold 模拟值。
p_diff = new_page_converted.mean() - old_page_converted.mean()
print(p_diff)
0.0002731376695282173
h. 使用**a. 到 g. ** 中的计算方法来模拟 10,000个 p n e w p_{new} pnew - p o l d p_{old} pold 值,并将这 10,000 个值存储在 p_diffs 中。
p_diffs = []
for _ in range(10000):new_page_converted = np.random.choice([0,1],size=n_new,p=[1-P_new, P_new])old_page_converted = np.random.choice([0,1],size=n_old,p=[1-P_old, P_old])p_diff = new_page_converted.mean() - old_page_converted.mean()p_diffs.append(p_diff)
i. 绘制一个 p_diffs 直方图。
p_diffs = np.array(p_diffs)
plt.hist(p_diffs)

j. 在p_diffs列表的数值中,有90.44%大于原数据 中观察到的实际差值
plt.hist(p_diffs)
obs_diff = df2[df2['group'] == 'treatment']['converted'].mean() - df2[df2['group'] == 'control']['converted'].mean()
plt.axvline(obs_diff, color='red')
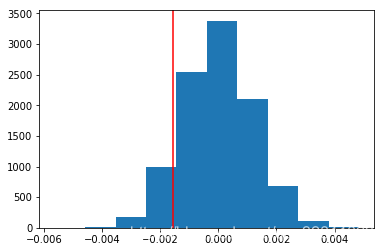
(p_diffs > obs_diff).mean()
0.9046
k. 在 **j.**中计算出来的结果,新旧页面的转化率有区别
- p-value = 0.9036.
- 根据p-value的值无法拒绝零假设.
l. 我们也可以使用一个内置程序 (built-in)来实现类似的结果。尽管使用内置程序可能更易于编写代码,但上面的内容是对正确思考统计显著性至关重要的思想的一个预排。填写下面的内容来计算每个页面的转化次数,以及每个页面的访问人数。使用 n_old 与 n_new 分别引证与旧页面和新页面关联的行数。
import statsmodels.api as smconvert_old = df2[df2['group']=='control']['converted'].sum()
convert_new = df2[df2['group']=='treatment']['converted'].sum()
n_old = df2[df2['group']=='control'].count()[0]
n_new = df2[df2['group']=='treatment'].count()[0]
m. 现在使用 stats.proportions_ztest 来计算你的检验统计量与 p-值。这里 是使用内置程序的一个有用链接。
z_score, p_value = sm.stats.proportions_ztest([convert_old, convert_new], [n_old, n_new], alternative='smaller')
print(z_score, p_value)
1.3109241984234394 0.9050583127590245
from scipy.stats import normprint(norm.cdf(z_score), norm.ppf(1-(0.05)))
0.9050583127590245 1.6448536269514722
n. * z-score 1.3109241984234394 < 1.6448536269514722, 在95%的置信区间上.
- 不能拒绝零假设,所以老页面转化率至少和新页面一样好.
- j 和 k 结果一致
III - 回归分析法之一
1. 之前的A / B测试中获得的结果也可以通过执行回归来获取。
a. 既然每行的值是转化或不转化,那么在这种情况下,我们应该使用逻辑回归
b. 目标是使用 statsmodels 来拟合你在 a. 中指定的回归模型,以查看用户收到的不同页面是否存在显著的转化差异。为每个用户收到的页面创建一个虚拟变量列。添加一个 截距 列,一个 ab_page 列,当用户接收 treatment 时为1, control 时为0。
df2[['control', 'treatment']] = pd.get_dummies(df2['group'])
df2['ab_page'] = df2['treatment']
c. 使用 statsmodels 导入回归模型。 实例化该模型,并使用你在 b. 中创建的2个列来拟合该模型,用来预测一个用户是否会发生转化。
df2['intercept'] = 1
logit_mod = sm.Logit(df2['converted'], df2[['intercept', 'ab_page']]) # logit模型拟合
results = logit_mod.fit()
Optimization terminated successfully.Current function value: 0.366118Iterations 6
d. 请在下方提供你的模型摘要,并根据需要使用它来回答下面的问题。
results.summary()
| Dep. Variable: | converted | No. Observations: | 290584 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 290582 |
| Method: | MLE | Df Model: | 1 |
| Date: | Mon, 08 Jul 2019 | Pseudo R-squ.: | 8.077e-06 |
| Time: | 22:31:55 | Log-Likelihood: | -1.0639e+05 |
| converged: | True | LL-Null: | -1.0639e+05 |
| LLR p-value: | 0.1899 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| intercept | -1.9888 | 0.008 | -246.669 | 0.000 | -2.005 | -1.973 |
| ab_page | -0.0150 | 0.011 | -1.311 | 0.190 | -0.037 | 0.007 |
e. p-value = 0.190,
- 零假设为ab_page = 0, 备择假设为 ab_page != 0. 与零假设和备择假设不同.所以导致p-value 不同.
f. 现在,你一定在考虑其他可能影响用户是否发生转化的因素。讨论为什么考虑将其他因素添加到回归模型中是一个不错的主意。在回归模型中添加附加项有什么弊端吗?
在这里给出你的答案。
单一元素对预测人的行为是困难的, 将其他因素添加到回归模型中可以更准确的预测人的行为.弊端是这些因素可能并不是相互独立的,可能相互之间会产生影响
g. 现在,除了测试不同页面的转化率是否会发生变化之外,还要根据用户居住的国家或地区添加一个 effect 项。
df_countries = pd.read_csv('countries.csv')
df_countries.head()
| user_id | country | |
|---|---|---|
| 0 | 834778 | UK |
| 1 | 928468 | US |
| 2 | 822059 | UK |
| 3 | 711597 | UK |
| 4 | 710616 | UK |
df3 = df_countries.set_index('user_id').join(df2.set_index('user_id'), how='inner')
df3.head()
| country | timestamp | group | landing_page | converted | control | treatment | ab_page | intercept | |
|---|---|---|---|---|---|---|---|---|---|
| user_id | |||||||||
| 834778 | UK | 2017-01-14 23:08:43.304998 | control | old_page | 0 | 1 | 0 | 0 | 1 |
| 928468 | US | 2017-01-23 14:44:16.387854 | treatment | new_page | 0 | 0 | 1 | 1 | 1 |
| 822059 | UK | 2017-01-16 14:04:14.719771 | treatment | new_page | 1 | 0 | 1 | 1 | 1 |
| 711597 | UK | 2017-01-22 03:14:24.763511 | control | old_page | 0 | 1 | 0 | 0 | 1 |
| 710616 | UK | 2017-01-16 13:14:44.000513 | treatment | new_page | 0 | 0 | 1 | 1 | 1 |
# 创建虚拟列
df3[['CA', 'UK', 'US']] = pd.get_dummies(df3['country'])
df3 = df3.drop(['CA'], axis=1)
# 逻辑回归
df3['intercept'] = 1
logit_mod = sm.Logit(df3['converted'], df3[['intercept', 'US', 'UK']])
results = logit_mod.fit() # logit模型拟合
results.summary()
Optimization terminated successfully.Current function value: 0.366116Iterations 6
| Dep. Variable: | converted | No. Observations: | 290584 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 290581 |
| Method: | MLE | Df Model: | 2 |
| Date: | Mon, 08 Jul 2019 | Pseudo R-squ.: | 1.521e-05 |
| Time: | 22:35:49 | Log-Likelihood: | -1.0639e+05 |
| converged: | True | LL-Null: | -1.0639e+05 |
| LLR p-value: | 0.1984 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| intercept | -2.0375 | 0.026 | -78.364 | 0.000 | -2.088 | -1.987 |
| US | 0.0408 | 0.027 | 1.518 | 0.129 | -0.012 | 0.093 |
| UK | 0.0507 | 0.028 | 1.786 | 0.074 | -0.005 | 0.106 |
- US和UK的p-value > 0.05, 说明国家差异对转化率影响不显著.
h. 考虑国家与页面在转化率上的个体性因素,但查看页面与国家/地区之间的相互作用,测试其是否会对转化产生重大影响。创建必要的附加列,并拟合一个新的模型。
df3['new_CA'] = df3['new_page'] * df3['CA']
df3['new_UK'] = df3['new_page'] * df3['UK']
df3['UK_ab_page'] = df3['UK'] * df3['ab_page']
df3.head()
| country | timestamp | group | landing_page | converted | control | treatment | ab_page | intercept | UK | US | UK_ab_page | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| user_id | ||||||||||||
| 834778 | UK | 2017-01-14 23:08:43.304998 | control | old_page | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 928468 | US | 2017-01-23 14:44:16.387854 | treatment | new_page | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 822059 | UK | 2017-01-16 14:04:14.719771 | treatment | new_page | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 711597 | UK | 2017-01-22 03:14:24.763511 | control | old_page | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 710616 | UK | 2017-01-16 13:14:44.000513 | treatment | new_page | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
# 逻辑回归
df3['intercept'] = 1
logit_mod = sm.Logit(df3['converted'], df3[['intercept', 'ab_page', 'US', 'UK', 'UK_ab_page']])
results = logit_mod.fit() # logit模型拟合
results.summary()
Optimization terminated successfully.Current function value: 0.366110Iterations 6
| Dep. Variable: | converted | No. Observations: | 290584 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 290579 |
| Method: | MLE | Df Model: | 4 |
| Date: | Mon, 08 Jul 2019 | Pseudo R-squ.: | 3.125e-05 |
| Time: | 22:36:47 | Log-Likelihood: | -1.0639e+05 |
| converged: | True | LL-Null: | -1.0639e+05 |
| LLR p-value: | 0.1557 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| intercept | -2.0257 | 0.027 | -75.518 | 0.000 | -2.078 | -1.973 |
| ab_page | -0.0236 | 0.013 | -1.785 | 0.074 | -0.049 | 0.002 |
| US | 0.0407 | 0.027 | 1.515 | 0.130 | -0.012 | 0.093 |
| UK | 0.0335 | 0.031 | 1.070 | 0.285 | -0.028 | 0.095 |
| UK_ab_page | 0.0344 | 0.026 | 1.306 | 0.192 | -0.017 | 0.086 |
- UK_ab_page p-value=0.192 > 0.05, 说明国家-页面的差异对转化率的影响不显著.
结论
- 不应该运行新页面



