1.lc77 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

https://leetcode.cn/problems/combinations/

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

//组合问题
//用过的不能再用，通过startindex实现
//每个元素只能取一次，通过dfs(satrtindex+1)实现class Solution {
private:vector<vector<int>> res;vector<int> path;void dfs(int n,int k,int startindex){if(path.size()==k) {res.push_back(path);return;}for(int i = startindex;i<=n;i++){path.push_back(i);dfs(n,k,i+1);path.pop_back();}}public:vector<vector<int>> combine(int n, int k) {dfs(n,k,1);return res;}
};

2.lc216 组合总和 III

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

https://leetcode.cn/problems/combination-sum-iii/

//组合问题
//要用startindex+1确保每个数字只用一次
//通过一维的path和二维的res保存中间结果和最后结果
//判断中止的条件时path中元素的个数是否达到k个
//通过判断path中元素的sum值来决定是否将path传到res
//dfs中需要传入k，n，startindex//疑问：需不需要一个变量记录path中已有变量的sumclass Solution {
private:vector<vector<int>> res;vector<int> path;void dfs(int k,int n,int startindex){if(path.size()==k) //决定树的深度{int sum = 0;for(int i = 0;i<k;i++){sum+=path[i];}if(sum==n) res.push_back(path);return;}for(int i = startindex;i<=9;i++)  //决定树的宽度{path.push_back(i);dfs(k,n,i+1);path.pop_back();}}public:vector<vector<int>> combinationSum3(int k, int n) {dfs(k,n,1);return res;}
};

3.lc17 电话号码的字母组合

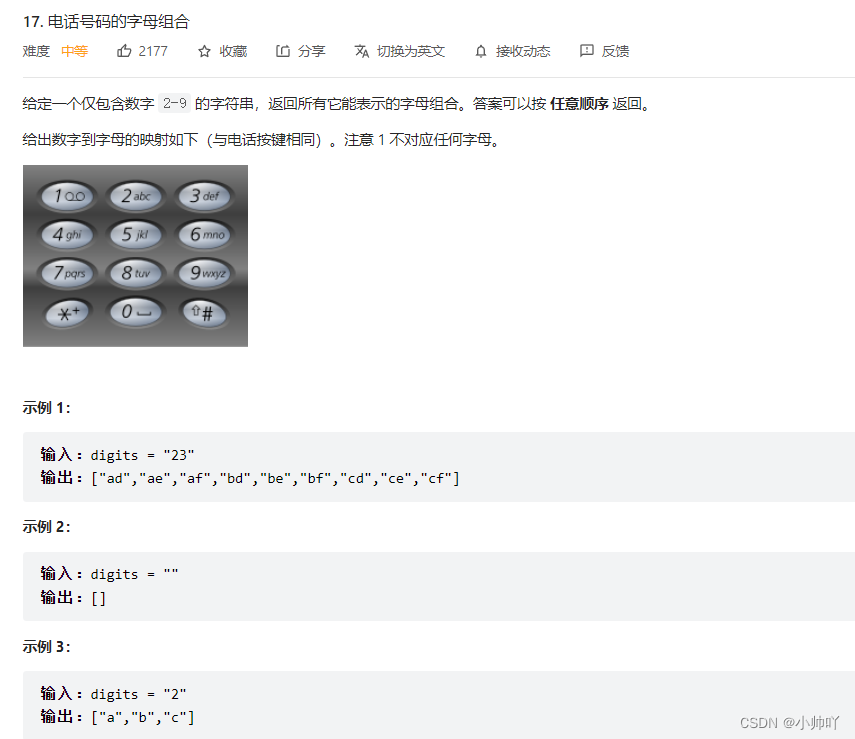
//首先要解决数字和对应字母之间的映射关系：定义一个string类型的数组来实现
//树的宽度为该层数字对应的字符串的长度，高度为digits的长度。
//要传入dfs的是digits，phone_map,index
//判断中止的条件是index为digits的长度class Solution {
private:vector<string> res;string path;const string phone_map[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};void dfs(string digits,int index){if(index==digits.size()){res.push_back(path);return;}for(int i = 0;i<phone_map[digits[index]-'0'].size();i++){path.push_back(phone_map[digits[index]-'0'][i]);dfs(digits,index+1);path.pop_back();}}public:vector<string> letterCombinations(string digits) {if(digits.size()==0) return res;dfs(digits,0);return res;}
};

4.lc39 组合总和

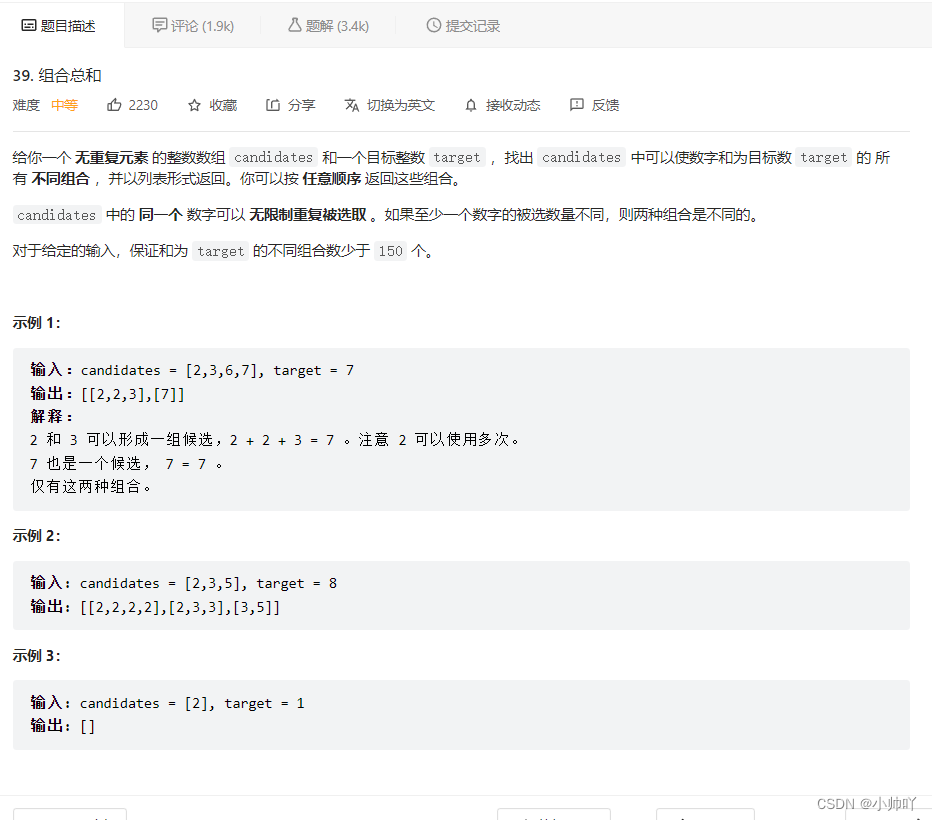
//依旧是组合问题，源数组无重复，但是可以重复选取
//和之前的"组合总和 III"主要区别在于源数组中的数能否重复的选取
//这个区别的话通过dfs中startindex不加1来实现
//这样的话中止条件需要通过path数组中已有元素的和是否超过target来判断
//为了实现实现上面的判断就需要在dfs中传入参数时，传入一个sum表示当前path的元素的和
//树的宽度为当前startindex下可以选取的元素数量class Solution {
private:vector<vector<int>> res;vector<int> path;void dfs(vector<int>& candidates,int target, int sum, int starindex){   if(sum>target) return;if(sum==target) {res.push_back(path);return;}for(int i = starindex;i<candidates.size();i++){sum+=candidates[i];path.push_back(candidates[i]);dfs(candidates,target,sum,i);sum-=candidates[i];path.pop_back();}}public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
//        dfs(candidates,target,sum,starindex);dfs(candidates,target,0,0);return res;}
};

5.lc40 组合总和 II

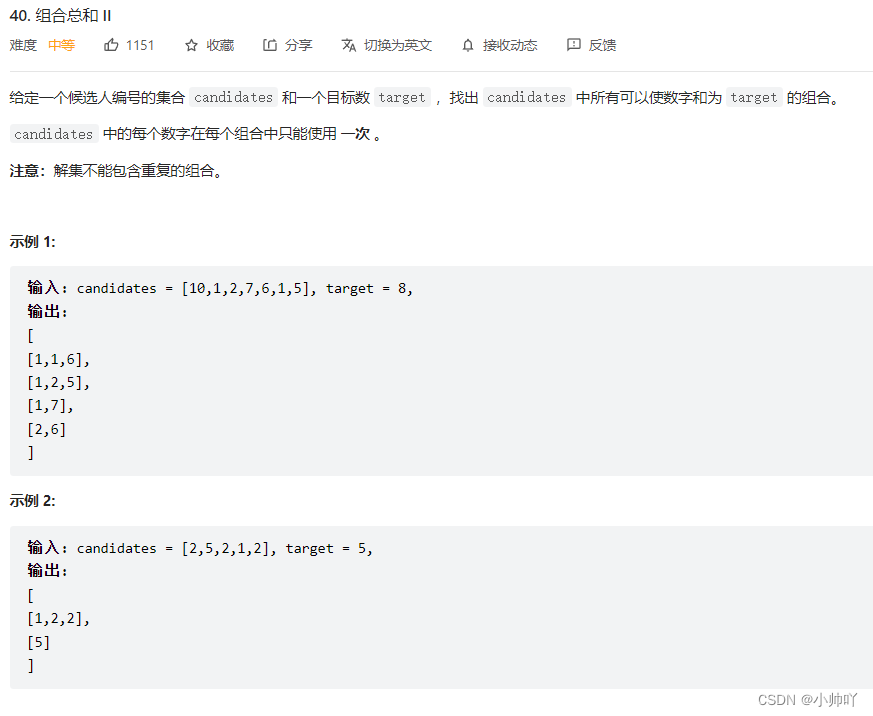
//这个跟上一个lc39 组合总和很像，区别在于本题源数组可以有重复，而对于数组中每个元素只可以取一次
//为了不重复还是需要用到startindex，到这里发现组合问题都需要startindex哈，到后面的排列问题就不需要了
//由于源数组中有重复元素，即使用了startindex依旧需要去重，这时如果考虑最后去重会花很多时间，可能导致超时吧
//于是乎，可以先对源数组排一下序，然后用一个used记录元素是否用过
//如果当前元素和前一个元素相等，而且used前一个元素时true代表什么呢？代表这俩在一个树枝上
//如果当前元素和前一个元素相等，而前一个元素used为false代表什么呢？代表这俩在同一层上
// 1 1 1 2 4 target=5 同一层上的情况直接跳过，因为它能贡献的情况，前面那个和他相同的值也能提供，并且提供更多
//树的宽度是startindex右边的数的大小，高度通过不限制但是sum超过target剪枝
//写代码时注意先排序，另外去掉同层的情况要写在循环中，

class Solution {vector<vector<int>> res;vector<int> path;void dfs(vector<int>& candidates,int target,vector<bool>& used,int sum, int startindex){if(sum>target) return;if(sum==target) {res.push_back(path);return;}for(int i = startindex;i<candidates.size();i++){if(i>0&&candidates[i-1]==candidates[i]&&used[i-1]==false)  continue;sum+=candidates[i];path.push_back(candidates[i]);used[i] = true;dfs(candidates,target,used,sum,i+1);sum-=candidates[i];path.pop_back();used[i] = false;}}
public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());vector<bool> used(candidates.size(), false);
//        dfs(candidates,target,sum,startindex)dfs(candidates,target,used,0,0);return res;}
};

6.lc131 分割回文串

//切割问题
//可切割的位置就是每个字符之后
//树的宽为startindex右边数量，深度不定
//终止条件根据startindex是否到最后一个元素后面确定
//一个很大的问题时如何表示分割线

//注：substr第一个参数是起始位置，第二个参数是长度

class Solution {
private:vector<vector<string>> res;vector<string> path;bool ishui(string s,int start,int end){bool flag = true;for(int i = start,j = end;i<j;i++,j--){if(s[i]!=s[j]) flag = false;}return flag;}void dfs(string s,int startindex){if(startindex==s.size()) {res.push_back(path);return;}for(int i = startindex;i<s.size();i++){if(ishui(s,startindex,i)){string str = s.substr(startindex,i-startindex+1);path.push_back(str);}else continue;dfs(s,i+1);path.pop_back();}}
public:vector<vector<string>> partition(string s) {//       dfs(s,startindex)dfs(s,0);return res;}
};

7.lc3 复原 IP 地址

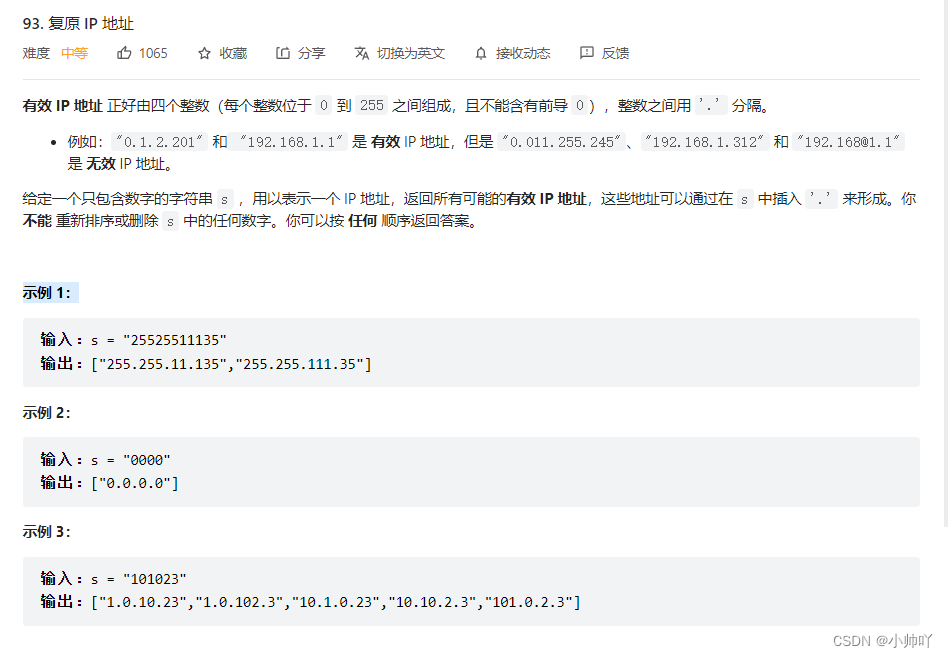
//复杂一点的分割问题
//在分割问题的基础上，区别在于要加dian
//对于加dian，要求每一段范围为0-255，且不含前导0
//要确保加三个点分成四段，还是通过startindex当作点,增加一个变量记录当前的点数
//树的宽度为startindex右边的数量，深度不定
//中止条件：indexnum等于3

class Solution {
private:vector<string> res;void dfs(string s, int startindex,int indexnum){if(indexnum==3){if(isValid(s,startindex,s.size()-1)) {res.push_back(s);}return ;}for(int i = startindex;i<s.size()-1;i++){if(isValid(s,startindex,i)){s.insert(s.begin()+i+1,'.');indexnum++;dfs(s,i+2,indexnum);indexnum--;s.erase(s.begin()+i+1);}else break;}}bool isValid(string s,int start,int end){if(start>end) return false;if (s[start] == '0' && start != end) { // 0开头的数字不合法return false;}int num = 0;for(int i=start;i<=end;i++){if(s[i]-'0'>9 || s[i]-'0'< 0) return false;num= num*10 + (s[i]-'0');if(num>255) return false;}return true;}public:vector<string> restoreIpAddresses(string s) {
//        dfs(s,startindex,indexsum);if (s.size() < 4 || s.size() > 12) return res;dfs(s,0,0);return res;}
};

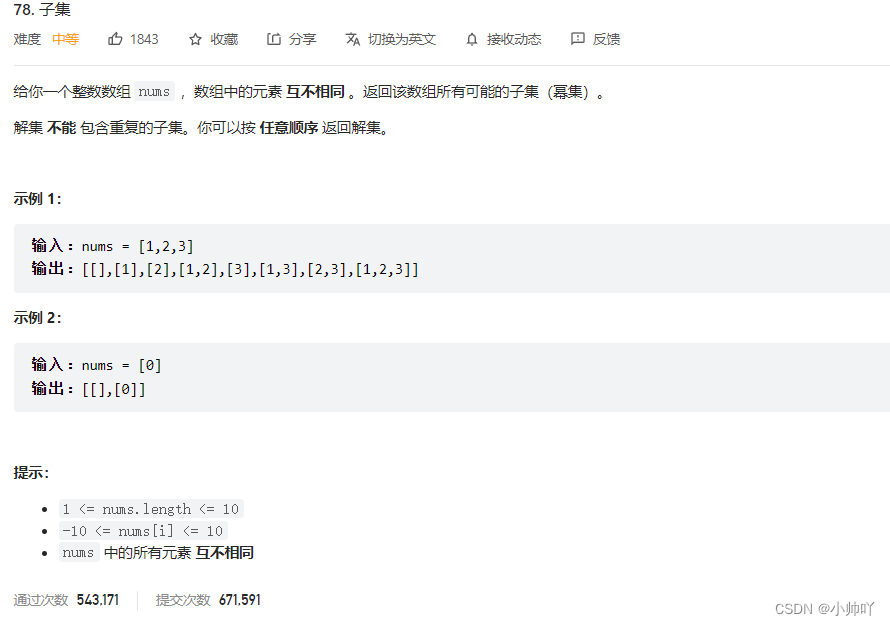
8.lc78 子集

//子集问题
//在组合问题基础上，需要将每个节点的结果保存下来
//回顾一下组合问题用startindex确保不重复，dfs的时候加1

class Solution {
private:vector<vector<int>> res;vector<int> path;void dfs(vector<int> nums,int startindex){res.push_back(path);if(startindex==nums.size()){return;}for(int i = startindex;i<nums.size();i++){path.push_back(nums[i]);dfs(nums,i+1);path.pop_back();}}
public:vector<vector<int>> subsets(vector<int>& nums) {//       dfs(nums,startindex);dfs(nums,0);return res;}
};

9.lc90 子集 II

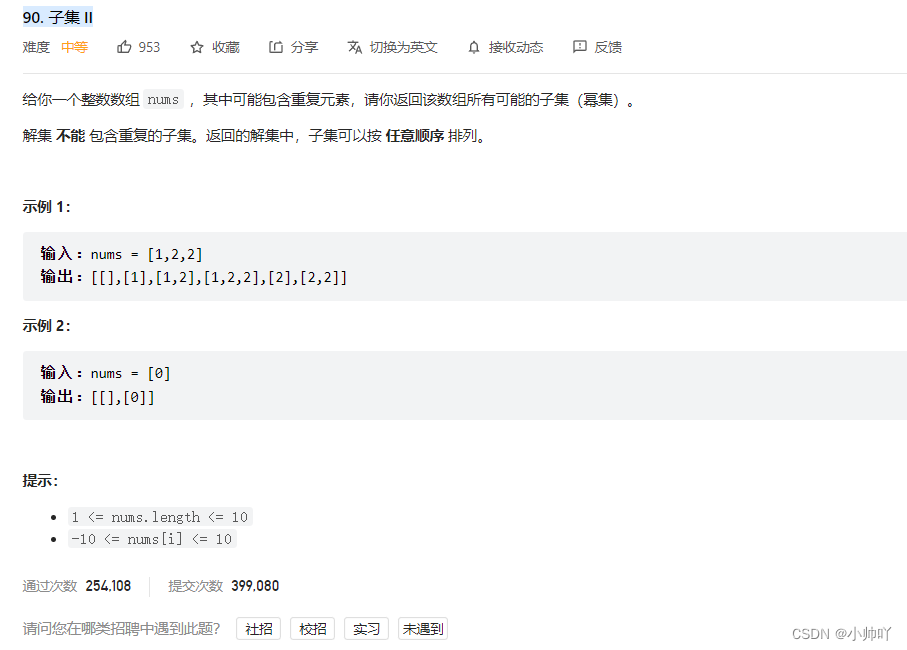
//还是子集问题，区别在于这次源数组中可以有重复元素，需要加入used数组，排序方式对结果去重

class Solution {
public:vector<vector<int>> res;vector<int> path;void dfs(vector<int>& nums,vector<bool>& used,int startindex){res.push_back(path);if(startindex==nums.size()) return;for(int i = startindex;i<nums.size();i++){if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) continue;path.push_back(nums[i]);used[i]=true;dfs(nums,used,i+1);path.pop_back();used[i] = false;}}vector<vector<int>> subsetsWithDup(vector<int>& nums) {vector<bool> used(nums.size(),false);sort(nums.begin(),nums.end());//       dfs(nums,used,startindex);dfs(nums,used,0);return res;}
};

10.lc491 递增子序列

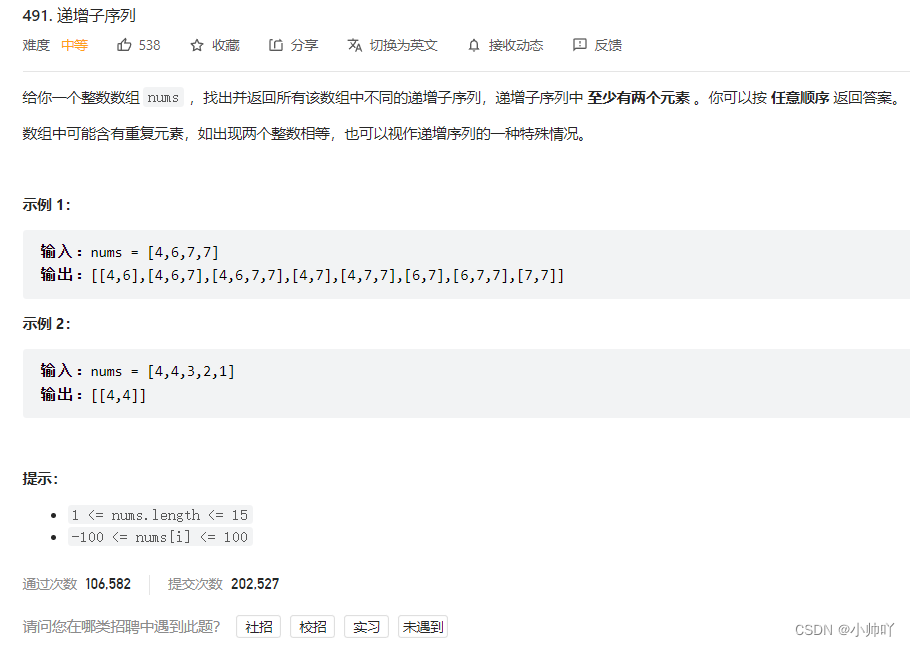
//和前面的子集问题十分类似
//要注意的是不能对数组进行排序，那么怎么实现去重呢，方法就是用一个哈希表存同一层的树结点
//当判断是否要往一个path中加数据时，要看当前值和path中最后一个数的大小的比较以及看同层是否出现过该数值

class Solution {
private:vector<vector<int>> res;vector<int> path;void dfs(vector<int> nums,int startindex){if(path.size()>1) res.push_back(path);if(startindex==nums.size()) return ;unordered_set<int> u; //注意不要定义在循环中for(int i = startindex;i<nums.size();i++){if((!path.empty()&&nums[i]<path.back())||u.find(nums[i])!=u.end()) continue;else{u.insert(nums[i]);path.push_back(nums[i]);dfs(nums,i+1);path.pop_back();}}}public:vector<vector<int>> findSubsequences(vector<int>& nums) {
//        dfs(nums,startindex);dfs(nums,0);return res;}
};

11.lc46 全排列

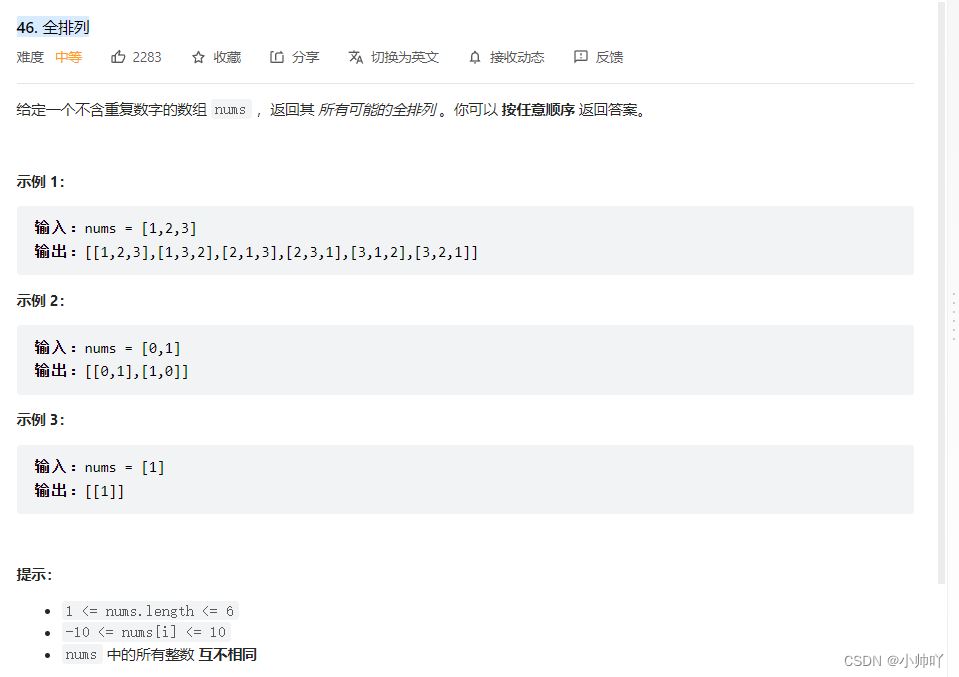
//排列问题
//不用startindex了
//那么如何去重呢，就需要用到used数组了我想，之前组合问题中对于源数组中有重复元素时用到used数组进行去重

class Solution {
private:vector<vector<int>> res;vector<int> path;void dfs(vector<int> nums,vector<bool> used,int u){if(u==nums.size()) {res.push_back(path);return ;}for(int i = 0;i<nums.size();i++){if(used[i]==false){path.push_back(nums[i]);used[i] = true;dfs(nums,used,u+1);used[i] = false;path.pop_back();}}}public:vector<vector<int>> permute(vector<int>& nums) {vector<bool> used(nums.size(),false);
//        dfs(nums,used,u);dfs(nums,used,0);return res;}
};

12.lc47 全排列 II

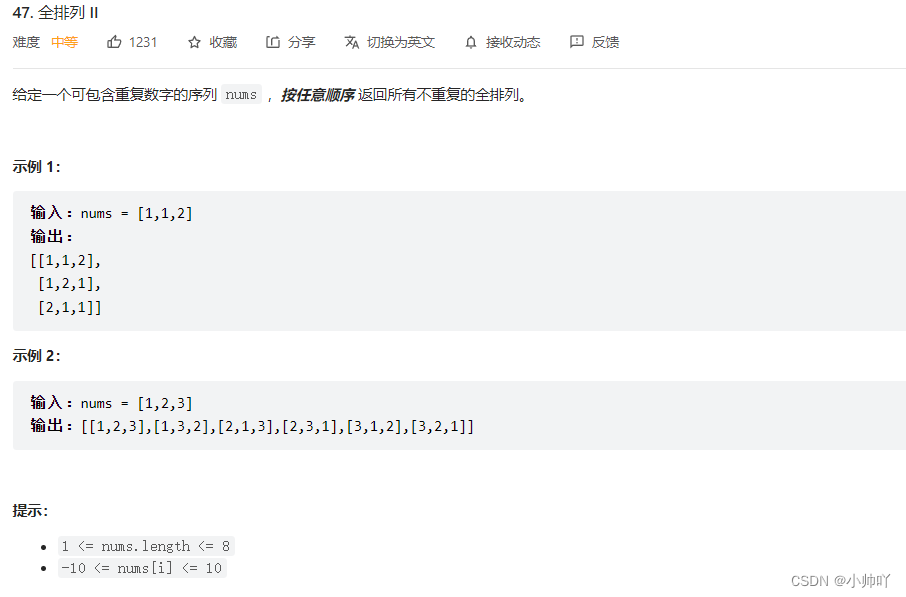
//全排列问题进阶，与上题不同在于源数组中有重复的元素
//如果还和上次那样的代码会出现什么问题呢，会出现重复

//怎么解决呢？初步想法是和组合问题中这种情况类似，先排序然后针对同层的元素用used数组判断是否要跳过

class Solution {
private:vector<vector<int>> res;vector<int> path;void dfs(vector<int> nums,vector<bool> used,int u){if(u==nums.size()) {res.push_back(path);return;}for(int i=0;i<nums.size();i++){if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) continue;if(used[i]==false) {path.push_back(nums[i]);used[i] = true;dfs(nums,used,u+1);used[i] = false;path.pop_back();}}}
public:vector<vector<int>> permuteUnique(vector<int>& nums) {vector<bool> used(nums.size(),false);sort(nums.begin(),nums.end());
//        dfs(nums,used,u);dfs(nums,used,0);return res;}
};

13.lc51 N 皇后

//主要是dg和udg数组的运用，dg和udg代表正负斜线的截距
//dg[u+i]即y = -x + b
//udg[u-i+n]即y = x+b 之所以加n是因为不然会出现负数的下标，这样都加n也可以一一对应上
//--------->
//|
//|
//|
//>

class Solution {
private:bool col[20],dg[20],udg[20];vector<vector<string>> res;vector<string> path;void dfs(int u,int n){if(u==n) {res.push_back(path);return;}for(int i = 0;i< n;i++){if(!col[i]&&!dg[u+i]&&!udg[u-i+n]){string s;for(int j = 0;j<n;j++){if(j==i) s+="Q";else s+=".";}path.push_back(s);col[i]=true;dg[u+i] = true;udg[u-i+n] =true;dfs(u+1,n);path.pop_back();col[i] = false;dg[u+i] = false;udg[u-i+n] = false;}else{continue;}}}public:vector<vector<string>> solveNQueens(int n) {dfs(0,n);return res;}
};

14.lc112 路径总和

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {int sum = 0;bool flag = false;void dfs(TreeNode* root, int targetSum){sum += root->val;if(root->left!=nullptr) hasPathSum(root->left,targetSum);if(root->right!=nullptr) hasPathSum(root->right,targetSum);if(root->left==nullptr&&root->right==nullptr) {if(sum==targetSum) flag = true;}sum-=root->val;}
public:bool hasPathSum(TreeNode* root, int targetSum) {if(root==nullptr) return false;dfs(root,targetSum);return flag;      }
};

15.lc113 路径总和 II

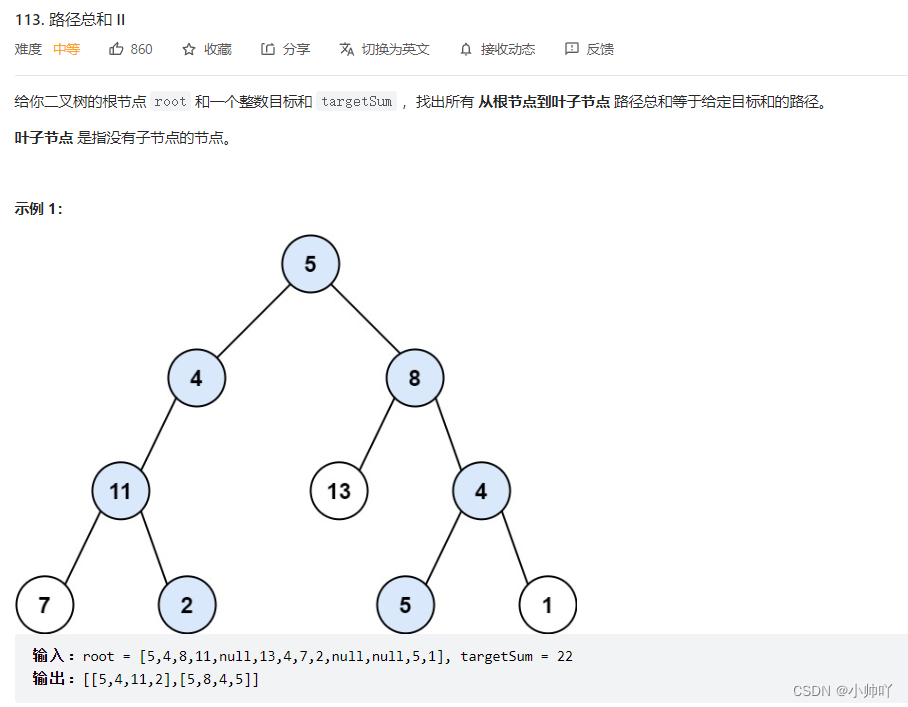
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*///和112.路径总和的区别在于要存一下路径//应该也不难，试一试
class Solution {
private:vector<vector<int>> res;vector<int> path;int sum = 0;void dfs(TreeNode* root, int targetSum){sum += root->val;path.push_back(root->val);if(root->left!=nullptr) dfs(root->left,targetSum);if(root->right!=nullptr) dfs(root->right,targetSum);if(root->left==nullptr&&root->right==nullptr) {if(sum==targetSum) {res.push_back(path);}}sum-=root->val;path.pop_back();}
public:vector<vector<int>> pathSum(TreeNode* root, int targetSum) {if(root==nullptr) return res;dfs(root,targetSum);return res;}
};

16.lc22 括号生成

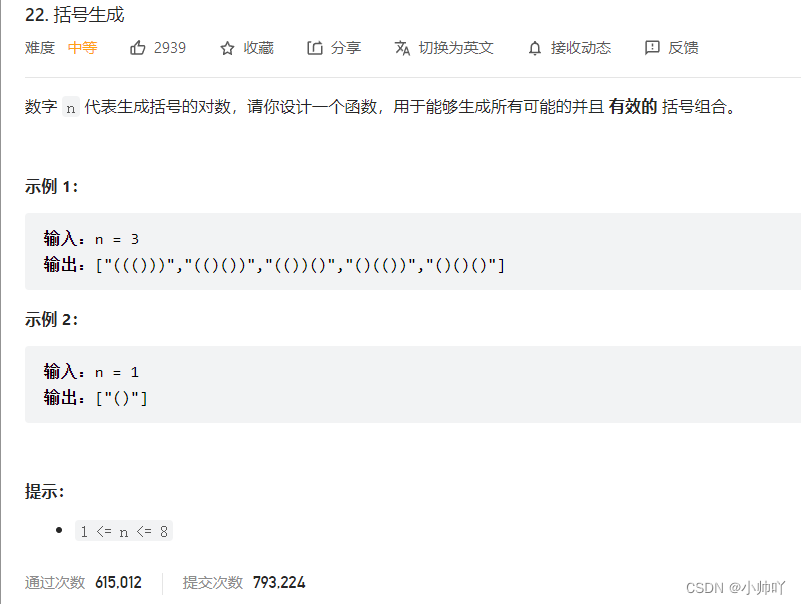
//dfs
//构建一个树形结构，树的宽度为2^n，树的深度为n*2
//剪枝：在生成结果过程中对于left>n(或者right>n的)或者right>left的要进行return

class Solution {
private:vector<string> res;int u = 0;string path;void dfs(int n,int u,int left,int right){if(left>n||right>left) return;if(u==2*n) {res.push_back(path);return;}path.push_back('(');dfs(n,u+1,left+1,right);path.pop_back();path.push_back(')');dfs(n,u+1,left,right+1);path.pop_back();}
public:vector<string> generateParenthesis(int n) {//dfs(n,u,right,left)dfs(n,0,0,0);return res;}
};

17.lc200 岛屿数量

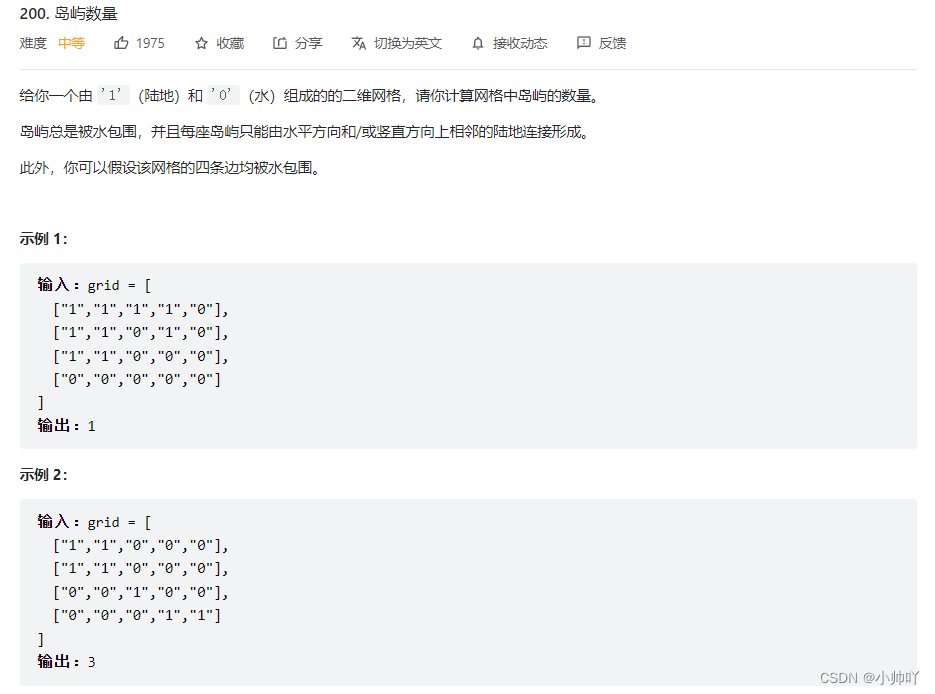
//用一个bool数组记录是否遍历过，遍历整个数组//类似对连着的染一下色，遍历的时候没到一个岛屿且没染色的话说明是一个独立的岛屿，最后得到结果class Solution {
public:bool used[310][310];void dfs(vector<vector<char>>& grid,int i,int j){int m = grid.size();int n = grid[0].size();used[i][j] = true;int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};for(int k=0;k<4;k++){int x = i+dx[k], y = j+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]=='1'&&used[x][y]==false){dfs(grid,x,y);}}return;}int numIslands(vector<vector<char>>& grid) {int res = 0;int m = grid.size();int n = grid[0].size();for(int i = 0;i<m;i++){for(int j = 0;j<n;j++){if(grid[i][j]=='1'&&used[i][j]==false) {res++;dfs(grid,i,j);}else continue;}}return res;}
};

18.lc79 单词搜索

//需要从每个位置开始遍历,该位置的字符不等与word[0]跳过
//需要用一个bool数组记录每个位置是否用过
//需要判断和word是否相同//用一个u记录当前层数，看与对应的word的索引下的字符是否相同class Solution {
public:bool flag = false;void dfs(vector<vector<char>>& board,string word,int u,bool used[7][7],int i,int j){if(u==word.size()) flag=true;int m = board.size();int n = board[0].size();int dx[4] = {0,0,1,-1}, dy[4] = {1,-1,0,0,};for(int k = 0;k<4;k++){int x =i + dx[k],y = j+dy[k];if(x>=0&&x<m&&y>=0&&y<n){if(board[x][y]==word[u]&&used[x][y]==false){used[x][y] = true;dfs(board,word,u+1,used,x,y);used[x][y] = false;}}}}bool exist(vector<vector<char>>& board, string word) {int m = board.size();int n = board[0].size();for(int i = 0;i<m;i++){for(int j =0;j<n;j++){if(board[i][j]==word[0]){bool used[7][7] = {false};used[i][j] = true;dfs(board,word,1,used,i,j); // dfs(board,word,u);}}}return flag;}
};