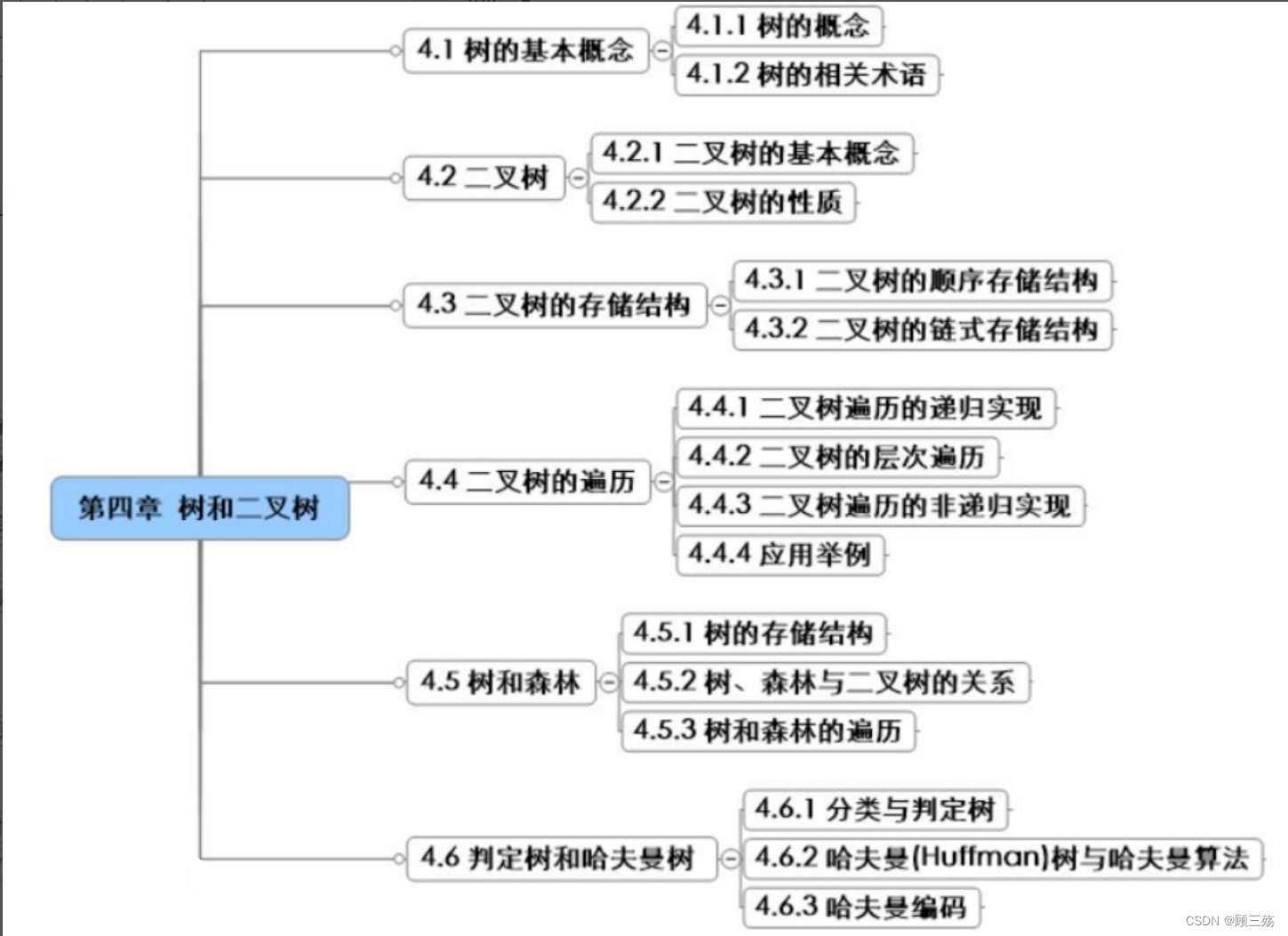
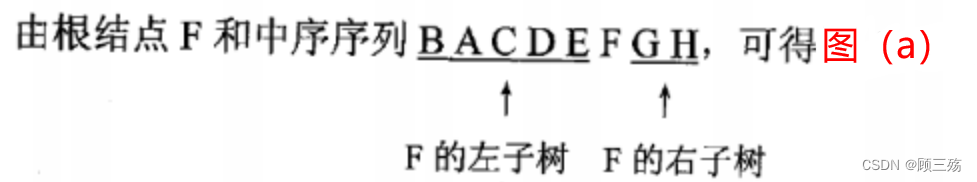目录
一、树的基本概念
(1)树的定义
(2)树的逻辑表示
(3)树的相关术语
(4)树的基本运算
二、二叉树
(1)二叉树的基本概念
① 定义
② 特点
③ 二叉树与树的比较
④ 二叉树的基本运算
(2)二叉树的性质
① 性质 1
② 性质 2
③ 性质 3
④ 性质 4
⑤ 性质 5
三、二叉树的存储结构
(1)二叉树的顺序存储结构
(2)二叉树的链式存储结构
四、二叉树的遍历
(1)遍历含义
(2)遍历规则
(3)遍历算法:二叉树遍历的递归实现
① 先序遍历(递归算法)
② 中序遍历运算(递归算法)
③ 后序遍历运算(递归算法)
(4)二叉树的层次遍历
(5)二叉树遍历的非递归实现
(6)应用举例
五、树和森林
(1)树的存储结构
① 双亲表示法
② 孩子链表表示法
Ⅰ. 双亲孩子表示法
③ 孩子兄弟链表表示法(二叉链表表示)
(2)树、森林与二叉树的关系
① 一般树 → 二叉树
② 森林 → 二叉树
③ 二叉树 → 一般树
(3)树和森林的遍历
① 树的遍历
② 森林的遍历
六、判定树和哈夫曼树
(1)分类与判定树
(2)哈夫曼树与哈夫曼算法
① 路径长度
② 哈夫曼树
③ 哈夫曼算法
④ 哈夫曼编码
一、树的基本概念
- 树型结构是一类重要的非线性结构。
- 树型结构是结点之间有分支, 并且具有层次关系的结构,它非常类似于自然界中的树。
- 树结构在客观 世界中是大量存在的,例如家谱、行政组织机构都可用树形象地表示。
- 树在计算机领域中也有着广泛的应用,例如在编译程序中,用树来表示源程序的语法结构;在数据库系统中,可用树来组织信息;在分析算法的行为时,可用树来描述其执行过程等等。
(1)树的定义
树 —— 是 n(n>=0) 个结点的有限集 T,满足:
- 当 n=0 时:称为空树
- 当 n>0 时:有且仅有一个特定的称为根的结点;其余的结点可分为 m(m>=0) 个互不相交的子集 T1,T2,T3…Tm,其中每个子集 Ti 又是一棵树,并称其为子树
(2)树的逻辑表示
一般表示法 (直观表示法):
(3)树的相关术语
- 结点:由一个数据元素及若干指向其它结点的分支所组成。
- 度:① 结点的度:所拥有的子树的数目。② 树的度:树中所有结点的度的最大值。
- 叶子(终端结点):度为 0 的结点。
- 非终端结点:度不为 0 的结点。
- 孩子(子结点):结点的子树的根称为该结点的孩子。
- 双亲(父结点):一个结点称为该结点所有子树根的双亲。
- 祖先:结点祖先指根到此结点的一条路径上的所有结点。
- 子孙:从某结点到叶结点的分支上的所有结点称为该结点的子孙。
- 兄弟:同一双亲的孩子之间互称兄弟。(父结点相同的结点)
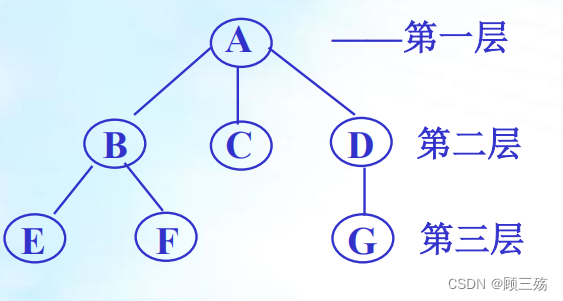
- 结点的层次:从根开始算起,根的层次为 1,其余结点的层次为其双亲的层次加 1。
- 堂兄弟:其双亲在同一层的结点。
- 树的深度(高度):一棵树中所有结点层次数的最大值。
- 有序树:若树中各结点的子树从左到右是有次序的,不能互换,称为有序树。
- 无序树:若树中各结点的子树是无次序的,可以互换,则成为无序树。
- 森林:是 m(≥0)棵树的集合。
(4)树的基本运算
➢ 求根 Root(T)
- 求树 T 的根结点
➢ 求双亲 Parent(T,X)
- 求结点 X 在树 T 上的双亲
- 若 X 是树 T 的根或 X 不在 T 上,则结果为一特殊标志
➢ 求孩子 Child(T,X,i)
- 求树 T 上结点 X 的第 i 个孩子结点
- 若 X 不在 T 上或 X 没有第 i 个孩子,则结果为一特殊标志;
➢ 建树 Create(X,T 1 ,…,T k ),k>1
- 建立一棵以 X 为根,以 T1 ,…,Tk 为第 1,…,k 棵子树的树
➢ 剪枝 Delete(T,X,i)
- 删除树 T 上结点X的第 i 棵子树
- 若 T 无第 i 棵子树,则为空操作
➢ 遍历 TraverseTree(T)
- 遍历树,即访问树中每个结点,且每个结点仅被访问一次
二、二叉树
二叉树在树结构的应用中起着非常重要的作用,因为二叉树有许多 良好的性质和简单的物理表示,而任何树都可以与二叉树相互转换,这 样就解决了树的存储结构及其运算中存在的复杂性。
(1)二叉树的基本概念
① 定义
二叉树 是 n(n>=0) 个结点的有限集合,它或为空 (n=0), 或是由一个 根 及 两棵 互不相交的 左子树和右子树 组成,且 中左子树和右子树也均为二叉树。
- 这是一个递归定义。
- 二叉树可以是空集合, 根可以有空的左子树或空的右子树。
② 特点
- 二叉树可以是空的,称空二叉树
- 每个结点最多只能有两个孩子
- 子树有左、右之分且次序不能颠倒
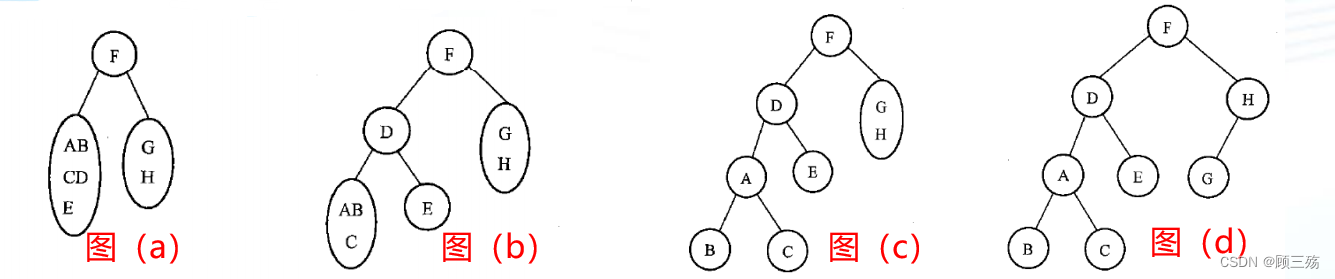
③ 二叉树与树的比较
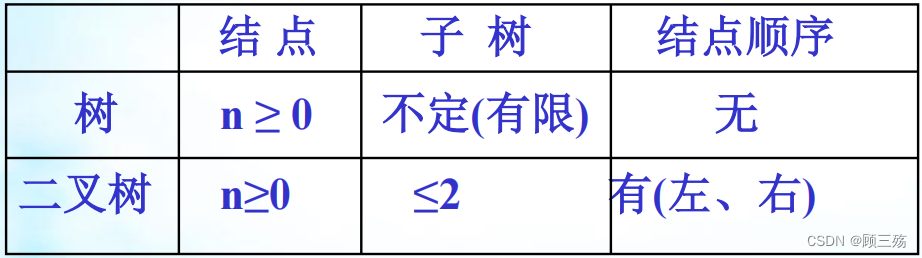

- 二叉树结点的子树要区分左子树和右子树,即使只有一棵子树也要进行区分,说明它是左子树,还是右子树。
- 这是二叉树与树的最主要的差别。
- 上图列出二叉树的 5 种基本形态,图 (c) 和(d)是不同的两棵二叉树。
④ 二叉树的基本运算
➢ 初始化 Initiate(BT)
- 建立一棵空二叉树,BT=∅
➢ 求双亲 Parent(BT,X)
- 求出二叉树 BT 上结点X的双亲结点
- 若 X 是 BT 的根或 X 根本不是 BT 上的结点,运算结果为 NULL
➢ 求左孩子 Lchild(BT,X) 和求右孩子 Rchild(BT,X)
- 分别求出二叉树 BT 上结点 X 的左、右孩子
- 若 X 为 BT 的叶子或 X 补在 BT 上,运算结果为 NULL
➢ 建二叉树 Create(BT)
- 建立一棵二叉树 BT
➢ 先序遍历 PreOrder(BT)
- 按先序对二叉树 BT 进行遍历,每个结点被访问一次且仅被访问一次
- 若 BT 为空,则运算为空操作
➢ 中序遍历 InOrder(BT)
- 按中序对二叉树 BT 进行遍历,每个结点被访问一次且仅被访问一次
- 若 BT 为空,则运算为空操作
➢ 后序遍历 PostOrder(BT)
- 按后序对二叉树 BT 进行遍历,每个结点被访问一次且仅被访问一次
- 若 BT 为空,则运算为空操作
➢ 层次遍历 LevelOrder(BT)
- 按层从上往下,同一层中结点按从左往右的顺序,对二叉树进行遍历,每个结点被访问一次且仅被访问一次
- 若 BT 为空,则运算为空操作
(2)二叉树的性质
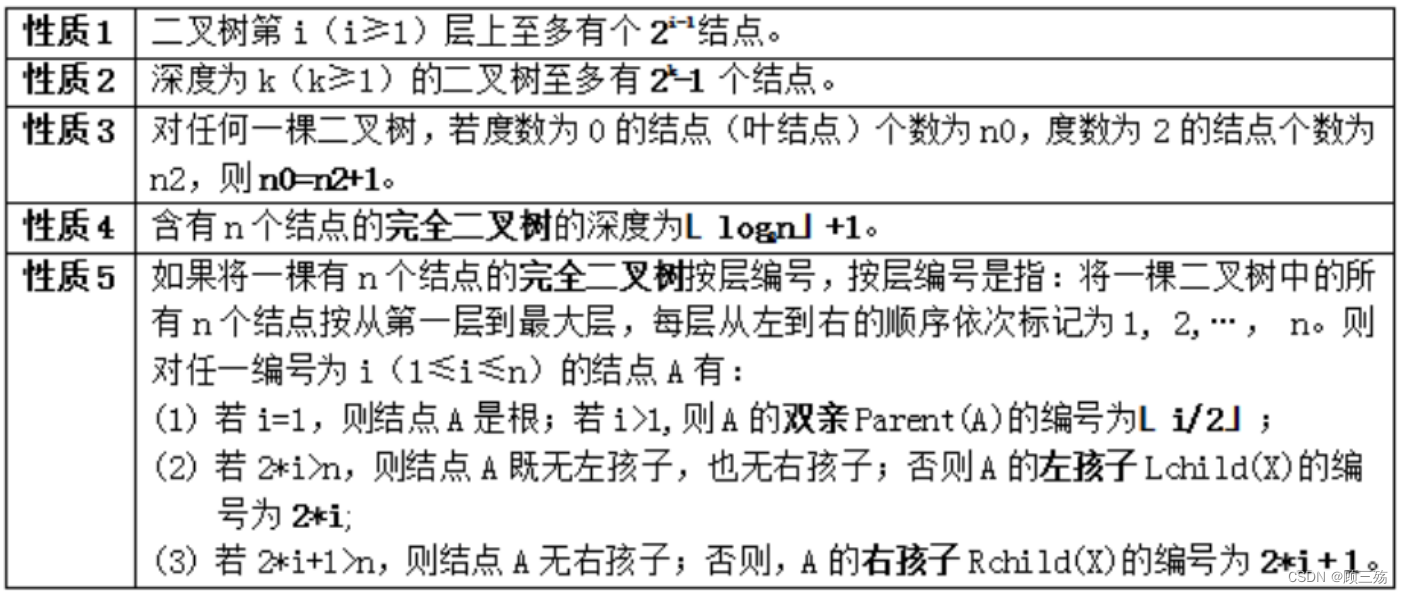
- 性质 1:二叉树的第 i 层最多有 2^(i-1) 个节点
- 性质 2:深度为 k 的二叉树最多有 2^k - 1 个节点
- 性质 3:在二叉树的第 i 层上,最多有 2^(i-1) 个节点
- 性质 4:具有 n 个节点的完全二叉树的高度为 ⌊log₂n⌋ + 1 或 ⌈log₂(n+1)⌉
- 性质 5:若任意二叉树的节点总数为 n,叶子节点数为 m,则 m = (n+1)/2
① 性质 1
【性质 1】 在二叉树的第 i(i>=1) 层上至多有 2^( i-1) 个 结点。
- 示例:在二叉树的第 5 层上至多有 2^(5-1) = 2^4 = 2*2*2*2 = 16 个结点
② 性质 2
【性质 2】 深度为 k(k>=1) 的二叉树至多有 2^ k - 1 个 结点。
- 示例:深度为 5 的二叉树至多有 2^5 - 1 = 2*2*2*2*2 - 1 = 32 - 1 = 31 个结点
③ 性质 3
【性质 3】 对任何一棵二叉树,如果其终端结点数为 n₀ (下标为 0 的 n) ,度为 2 的结点数为 n₂ ,则 n₀=n₂+1 。即: 叶结点数 n₀ = 度为 2 的结点数 n₂+1
- 根据定义,二叉树中的每个非叶节点最多可以有两个孩子节点,因此它的度为 2 的结点数就是有两个孩子节点的结点数。
- 根据二叉树的性质,每个非叶节点都有两个子节点,就表示了 2 个子节点的个数,而终端结点是没有子节点的,因此,终端结点数(叶结点数)就是度为 2 的结点数(有两个子节点的结点数)加 1。
- 所以,对于任意一棵二叉树,叶结点数(终端结点数)等于度为 2 的结点数(有两个子节点的结点数)加 1。
【示例】 考虑以下二叉树:
A/ \B C/ \ D E/ \F G在这个二叉树中,共有 6 个终端结点(叶结点)和 5 个度为 2 的结点(具有两个子节点的结点)。
- 终端结点(n₀) = 6
- 度为 2 的结点数(n₂) = 5
根据关系 n₀ = n₂ + 1,我们有:
- 6 = 5 + 1
- 6 = 6
在这个实例中,这个关系成立,终端结点数等于度为 2 的结点数加 1 。
请注意,这个关系并不是对于所有二叉树都成立,它仅在特定情况下成立。

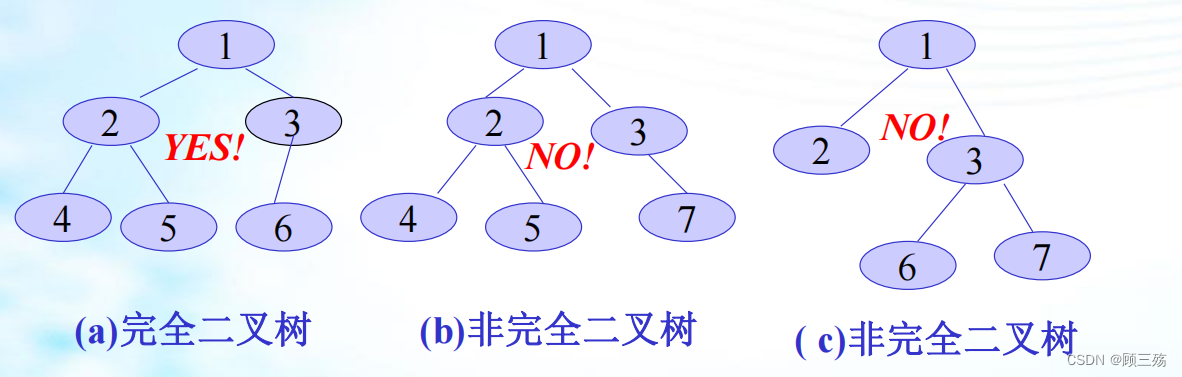
满二叉树 : 深度为 k (k >= 1) 且有 2^k - 1 个结点的二叉树。满二叉树中 结点顺序编号 : 即从第一层结点开始自上而下,从左到右进行连续编号。
完全二叉树 : 深度为 k 的二叉树中,k - 1 层 结点数是满的 2^(k-2) ,k 层结点是左连续的(即结点编号是连续的)。 如下图(a)注:满二叉树是完全二叉树的特例。
④ 性质 4
【性质 4】 具有 n 个结点的完全二叉树的深度为 [log₂n] + 1
- 符号 [x] 表示不大于 x 的最大整数。
- 假设此二叉树的深度为 k,则根据性质 2 及完全二叉树的定义得到:
2^(k-1) - 1 < n <= 2^k - 1 // 或: 2^(k-1) <= n < 2^k
- 取对数得到:k-1 < log₂n < k 因为 k 是整数,所以有:
k= [log₂n] + 1
⑤ 性质 5
【性质 5】 对有 n 个结点的完全二叉树的结点按层编号 ( 从第 1 层到第 [log₂n] + 1 层,每层从左到右 ), 则对任一结点 i(1 ≤ i ≤ n),有:
- 如果 i=1,则结点 i 无双亲,是二叉树的根; 如果 i > 1,则 i 的双亲 Parent(A) 是结点 [i/2];
- 如果 2*i ≤ n,则其左孩子是结点 2*i ,否则,结点 i 无左孩子且为叶子结点;
- 如果 2*i+1 ≤ n,则其右孩子是结点 2*i+1, 否则,结点 i 无右孩子。
三、二叉树的存储结构
(1)二叉树的顺序存储结构
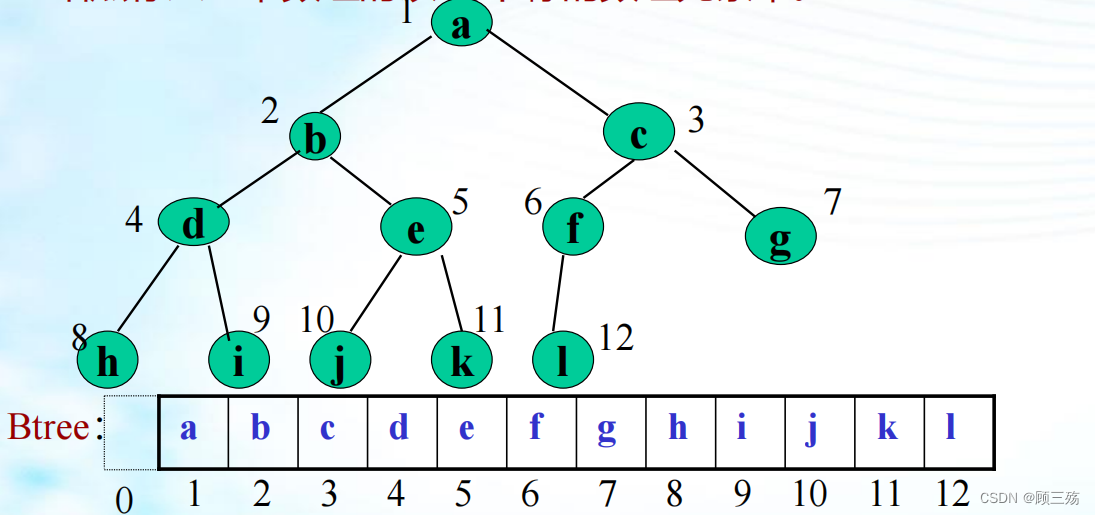
它是用一组连续的存储单元存储二叉树的数据元素。因此,必须把 二叉树的所有结点安排成为一个恰当的序列,结点在这个序列中的相 互位置能反映出结点之间的逻辑关系,可用编号的方法。
二叉树的顺序存储结构 : 即对二叉树按完全二 叉树进行编号,然后用一维数组存储,其中 编号 为 i 的结点存储在数组中 下标为 i 的分量中。—— 该方法称为 “以编号为地址” 策略
从树根起,自上层至下层,每层自左至右的给所有结点编号缺点是 有可能对存储空间造成极大的浪费,在最坏的情况下,一个深度为 H 且只有 H 个结点的右单支树却需要 2^ h - 1 个结点存储空间。而且,若经 常需要插入与删除树中结点时,顺序存储方式不是很好!
- 对于完全二叉树来说,采用以编号作为数组的下边的方法将结点存入一位数组中,也就是将编号为 i 的结点存入一维数组的以 i 为下标的数组元素中。
- 对于非完全二叉树,则用某种方法将其转化为完全二叉树,为此可增设若干个虚拟结点。
➢ 此方法用于完全二叉树
- 节省内存
- 结点位置确定方便

➢ 此方法用于一般二叉树
- 浪费空间
➢ 此方法用于单分支二叉树
- 存储空间浪费极大
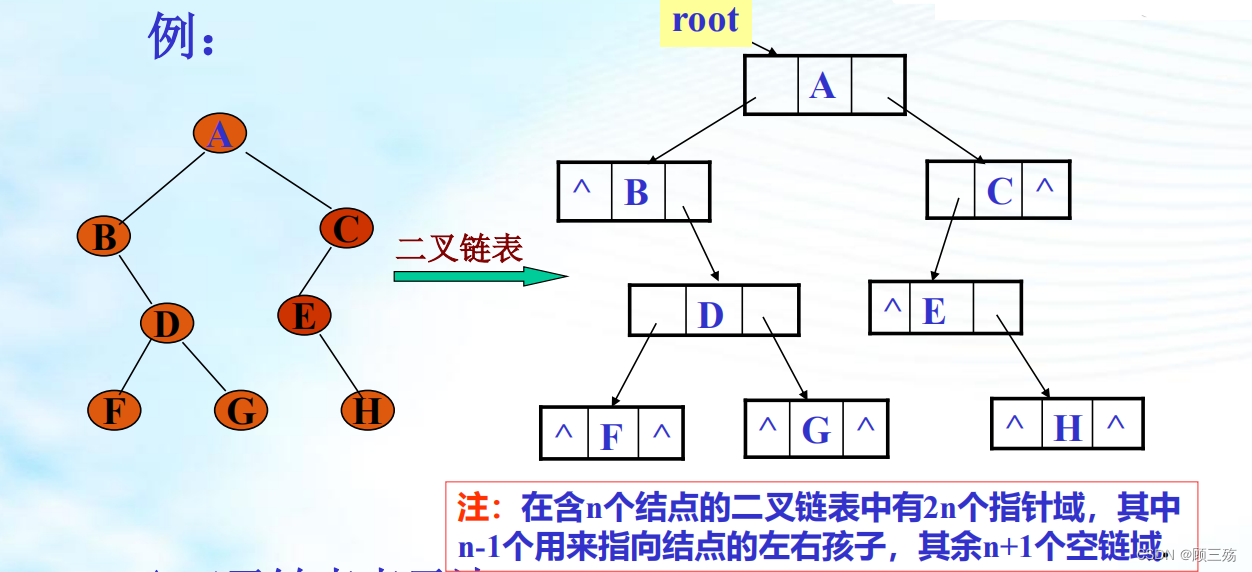
(2)二叉树的链式存储结构
【二叉链表表示法】

【二叉链表类型定义】二叉链表类型 :
typedef struct btnode {DataType data; // 存储的数据类型struct btnode *lchild; // 左子节点指针struct btnode *rchild; // 右子节点指针 } *BinTree;
- 这段代码定义了一个名为
btnode的结构体类型,并通过typedef关键字给它起了一个别名BinTree。btnode结构体包含了一个名为data的变量,用来存储数据类型DataType的值。- 此外,它还包含了两个指针变量
lchild和rchild,分别指向左子节点和右子节点。- 整个结构体定义结束后,通过
*BinTree实际上定义了一个指向btnode结构体的指针类型。- 这样,以后我们就可以使用
BinTree来声明二叉树的变量或参数,简化了代码的书写同时提高了可读性。
【三叉链表表示法】


四、二叉树的遍历
(1)遍历含义
在二叉树的一些应用中,常常要求在树中查找具有某种特征的结 点,或者对树中全部结点逐一进行某种处理。这就引入了遍历二叉 树的问题。
遍历二叉树 : 是指按 某种次序访问 二叉树上的 所有结点,使每个结点被 访问一次 且仅被访问一 次。
(2)遍历规则
由二叉树的递归定义知,二叉树 的三个基本组成单元是:根结点、 左子树和右子树。
(3)遍历算法:二叉树遍历的递归实现



① 先序遍历(递归算法)
先序遍历 DLR : 首 先 访问 根 结点, 其次 遍历 根的 左子树 , 最后 遍历根 右子树 ,对每棵子树同样按 这三步( 先根、后左、再右 )进行。
步骤: 若二叉树为空,执行空操作; 否则 :
- 访问根结点
- 先序遍历左子树
- 先序遍历右子树
算法:
void preorder(BinTree bt) {/* 先序遍历以bt为根的二叉树 */if (bt != NULL){visit(bt); // 访问根结点preorder(bt->lchild); // 递归先序遍历左子树preorder(bt->rchild); // 递归先序遍历右子树} }
- 这段代码定义了一个
preorder函数,用于先序遍历以bt为根的二叉树。先序遍历的具体步骤是:先访问根结点,然后递归地对左子树进行先序遍历,最后递归地对右子树进行先序遍历。- 在函数定义中,我们使用了结构体指针
BinTree表示二叉树,bt参数是一个指向二叉树根节点的指针。- 在函数体中,首先,通过条件判断语句
if (bt != NULL)来判断当前节点是否为空,如果不为空,则执行先序遍历的操作。- 在非空节点的情况下,先调用了
visit(bt)来访问当前根结点,这里的visit()可以表示对根结点进行具体操作的函数。- 然后,接着递归调用
preorder(bt->lchild)对左子树进行先序遍历,bt->lchild表示当前节点的左子节点。- 最后,再递归调用
preorder(bt->rchild)对右子树进行先序遍历,bt->rchild表示当前节点的右子节点。- 通过以上代码,可以实现先序遍历以
bt为根的二叉树的功能。- 注意需要在代码中实现
visit()函数来具体处理对每个节点的操作。
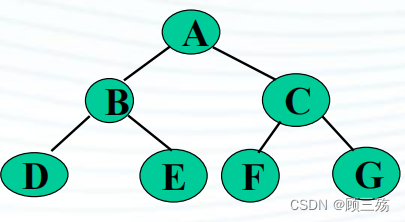
② 中序遍历运算(递归算法)
中序遍历 LDR : 首 先 遍历根的 左子树 , 其次 访问 根 结点, 最后 遍历根 右子树 ,对每棵子树同样按 这三步( 先左、后根、再右 )进行。
步骤: 若二叉树为空,执行空操作; 否则 :
- 中序遍历左子树
- 访问根结点
- 中序遍历右子树
算法:
void inorder(BinTree bt) {/* 中序遍历以bt为根的二叉树 */if (bt != NULL){inorder(bt->lchild); // 递归中序遍历左子树visit(bt); // 访问根结点inorder(bt->rchild); // 递归中序遍历右子树} }
- 这段代码定义了一个
inorder函数,用于中序遍历以bt为根的二叉树。中序遍历的具体步骤是:先递归地对左子树进行中序遍历,然后访问根结点,最后递归地对右子树进行中序遍历。- 在函数定义中,我们使用了结构体指针
BinTree表示二叉树,bt参数是一个指向二叉树根节点的指针。- 在函数体中,首先,通过条件判断语句
if (bt != NULL)来判断当前节点是否为空,如果不为空,则执行中序遍历的操作。- 在非空节点的情况下,先调用了
inorder(bt->lchild)递归地对左子树进行中序遍历,bt->lchild表示当前节点的左子节点。- 然后,访问根结点,使用
visit(bt)来对当前根结点进行访问,这里的visit()可以表示对根结点进行具体操作的函数。- 最后,再递归调用
inorder(bt->rchild)递归地对右子树进行中序遍历,bt->rchild表示当前节点的右子节点。- 通过以上代码,可以实现中序遍历以
bt为根的二叉树的功能。注意需要在代码中实现visit()函数来具体处理对每个节点的操作。
③ 后序遍历运算(递归算法)
后序遍历 LRD : 首 先 遍历根的 左子树 , 其次 遍历根的 右子树 , 最后 访问 根 结点,对每棵子树同样 按这三步( 先左、后右、最后根 )进行。
步骤: 若二叉树为空,则退出; 否则 :
- 后序遍历根的左子树
- 后序遍历根的右子树
- 访问根结点
算法:
void postorder(BinTree bt) {/* 后序遍历以bt为根的二叉树 */if (bt != NULL){postorder(bt->lchild); // 后序遍历以左孩子为根的左子树postorder(bt->rchild); // 后序遍历以右孩子为根的右子树visit(bt); // 访问根结点} }
- 这段代码定义了一个
postorder函数,用于后序遍历以bt为根的二叉树。后序遍历的具体步骤是:先后序遍历左子树,然后后序遍历右子树,最后访问根结点。- 在函数定义中,我们使用了结构体指针
BinTree表示二叉树,bt参数是一个指向二叉树根节点的指针。- 在函数体中,首先,通过条件判断语句
if (bt != NULL)来判断当前节点是否为空,如果不为空,则执行后序遍历的操作。- 在非空节点的情况下,先调用了
postorder(bt->lchild)后序遍历以左孩子为根的左子树,bt->lchild表示当前节点的左子节点。- 然后,调用
postorder(bt->rchild)后序遍历以右孩子为根的右子树,bt->rchild表示当前节点的右子节点。- 最后,调用
visit(bt)来访问根结点,这里的visit()可以表示对根结点进行具体操作的函数。- 通过以上代码,可以实现后序遍历以
bt为根的二叉树的功能。注意需要在代码中实现visit()函数来具体处理对每个节点的操作。
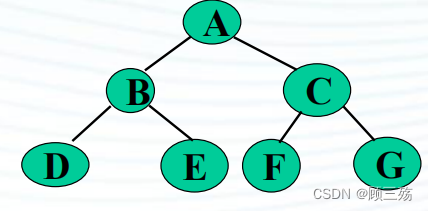
对于如下图的二叉树,其先序、中序、后序遍 历的序列为:

- 先序遍历:A、B、D、F、G、C、E、H
- 中序遍历:B、F、D、G、A、C、E、H
- 后序遍历:F、G、D、B、H、E、C、A
任意一棵二叉树的前序和后序遍历的结果序列中, 各叶子结点之间的相对次序关系 都相同 。二叉树的遍历大概分为四种,分别是:
- 前序遍历
- 中序遍历
- 后序遍历
- 按层遍历

1. 先序遍历
- 原则:根 → 左 → 右
- 先序输出:A B D G H E C K F I J
2. 中序遍历
- 原则:左 → 根 → 右
- 中序输出:G D H B E A K C I J F
3. 后序遍历
- 原则:左 → 右 → 根
- 后序输出:G H D E B K J I F C A
4. 按层遍历
- 原则:从上到下,从左到右
- 按层输出:A B C D E K F G H l J
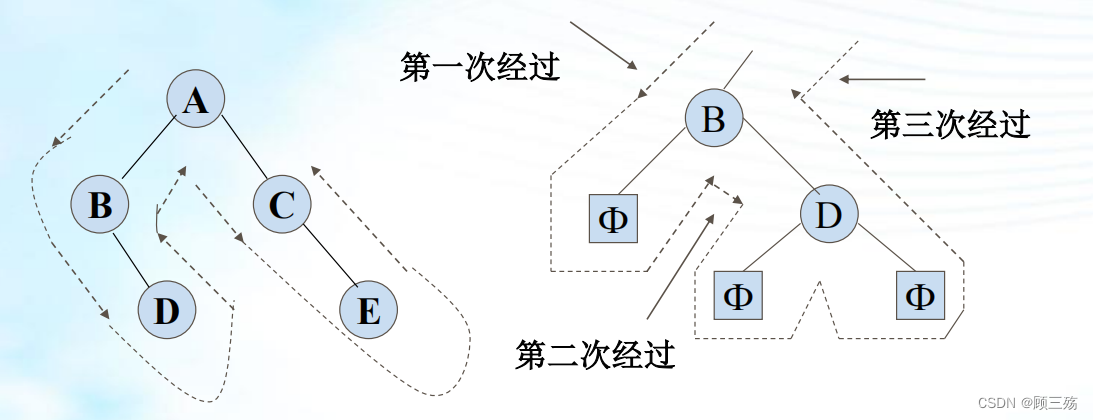
以中序遍历为例来说明中序遍历二叉树的递归过程:
(4)二叉树的层次遍历
二叉树的层次遍历: 从二叉树的 根结点 的这一层开始,逐层向下 遍历,在每一层上按从左到右的顺序对结点逐个访问。
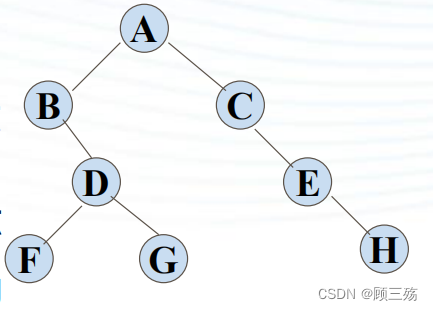 上图按照层次遍历,所得到的 的结点序列为: A B C D E F G H设立一个队列 Q ,用于存放结点,以保证二叉树结点 按照层次顺序从左往右进入队列。若二叉树 bt 非空:
上图按照层次遍历,所得到的 的结点序列为: A B C D E F G H设立一个队列 Q ,用于存放结点,以保证二叉树结点 按照层次顺序从左往右进入队列。若二叉树 bt 非空:
- 将根结点插入队列
- 从队列中删除一个结点,访问该结点,并将该结点的孩子(若有的话)插入队列
- 若此时队列非空,再从队列中删除一个结点,访问该结点,并将它的孩子结点插入队列。依次重复进行,直到队列为空。
【示例代码】
// 层序遍历函数 void levelorder(BinTree bt) {LkQue Q;InitQueue(&Q);// 非空树才进行遍历if (bt != NULL) {EnQueue(&Q, bt);// 队列非空时循环while (!EmptyQueue(Q)){p = Gethead(&Q);outQueue(&Q);visit(p);// 将左子树入队if (p->lchild != NULL) EnQueue(&Q, p->lchild);// 将右子树入队if (p->rchild != NULL) EnQueue(&Q, p->rchild);}} }【代码详解】
- 代码的作用是对给定的二叉树进行层序遍历,即按层从上到下逐个访问二叉树的节点,并按照每层从左到右的顺序进行访问。
void levelorder(BinTree bt): 定义了一个名为levelorder的函数,参数类型为BinTree。
LkQue Q;: 声明了一个名为Q的队列变量,类型为LkQue。
InitQueue(&Q);: 对队列Q进行初始化操作。
if (bt != NULL): 判断传入的二叉树bt是否为空。
EnQueue(&Q, bt);: 将二叉树的根节点入队。
while (!EmptyQueue(Q)): 当队列非空时,循环执行以下操作。
p = Gethead(&Q);: 取出队头元素,并将其赋值给变量p。
outQueue(&Q);: 将队头元素出队。
visit(p);: 对当前节点p进行访问操作。
if (p->lchild != NULL) EnQueue(&Q, p->lchild);: 如果当前节点的左子树不为空,将左子树入队。
if (p->rchild != NULL) EnQueue(&Q, p->rchild);: 如果当前节点的右子树不为空,将右子树入队。
(5)二叉树遍历的非递归实现
二叉树的非递归遍历可以利用栈作为辅助数据结构,通过迭代的方式来实现。
【示例代码】以下是二叉树的三种遍历方式(前序、中序、后序)的非递归实现代码:
#include <iostream> #include <stack> using namespace std;// 二叉树节点结构 struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(NULL), right(NULL) {} };// 前序遍历(非递归) void preorderTraversal(TreeNode* root) {stack<TreeNode*> st;TreeNode* node = root;while (node != NULL || !st.empty()) {while (node != NULL) {// 输出节点值cout << node->val << " ";st.push(node);node = node->left;}if (!st.empty()) {node = st.top();st.pop();node = node->right;}} }// 中序遍历(非递归) void inorderTraversal(TreeNode* root) {stack<TreeNode*> st;TreeNode* node = root;while (node != NULL || !st.empty()) {while (node != NULL) {st.push(node);node = node->left;}if (!st.empty()) {node = st.top();st.pop();// 输出节点值cout << node->val << " ";node = node->right;}} }// 后序遍历(非递归) void postorderTraversal(TreeNode* root) {stack<TreeNode*> st;TreeNode* node = root;TreeNode* lastVisited = NULL;while (node != NULL || !st.empty()) {while (node != NULL) {st.push(node);node = node->left;}if (!st.empty()) {node = st.top();// 检查当前节点的右子树是否已访问过if (node->right == NULL || node->right == lastVisited) {st.pop();// 输出节点值cout << node->val << " ";lastVisited = node;node = NULL;} else {node = node->right;}}} }【代码详解】
- 这里使用了一个栈
st来暂存待访问的节点,然后根据不同的遍历顺序,先将左子树节点入栈,再访问根节点,最后访问右子树节点。注意,在后序遍历中,需要增加一个lastVisited变量来判断右子树是否已经访问过。这样,通过栈的辅助,可以实现二叉树的非递归遍历。
#include <iostream>:包含了输入输出流的头文件。
#include <stack>:包含了栈的头文件。
struct TreeNode:定义了二叉树的节点结构,包括一个值val,以及左右子树的指针。
void preorderTraversal(TreeNode* root):前序遍历的非递归实现函数。
void inorderTraversal(TreeNode* root):中序遍历的非递归实现函数。
void postorderTraversal(TreeNode* root):后序遍历的非递归实现函数。对于每个遍历函数,首先声明一个栈
stack<TreeNode*> st,并初始化根节点指针node为传入的根节点。
while (node != NULL || !st.empty()):当当前节点不为空或栈非空时,继续遍历。内层
while循环用于将左子树节点入栈,直到当前节点为空。这样可以保证在回溯时,能够访问到该节点的右子树。
if (!st.empty()):如果栈非空,则取出栈顶节点并弹出,然后将当前节点指针node赋值为栈顶节点的右子节点。在前序和中序遍历中,输出当前节点的值
cout << node->val << " ";。在后序遍历中,需要额外判断当前节点的右子树是否已经被访问过。如果是,则表示该节点的左右子树都已经访问过,可以输出该节点的值,并将
lastVisited指针指向当前节点,将node置空。否则,将node指针更新为当前节点的右子节点。【代码调用】 可以根据需要调用相应的遍历函数来进行测试,例如:
int main() {// 创建一棵二叉树TreeNode* root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);root->left->left = new TreeNode(4);root->left->right = new TreeNode(5);// 前序遍历cout << "Preorder Traversal: ";preorderTraversal(root);cout << endl;// 中序遍历cout << "Inorder Traversal: ";inorderTraversal(root);cout << endl;// 后序遍历cout << "Postorder Traversal: ";postorderTraversal(root);cout << endl;return 0; }【调用说明】
int main():程序入口函数。创建一棵二叉树,根节点的值为 1,左子节点的值为 2,右子节点的值为 3,左子树的左子节点的值为 4,左子树的右子节点的值为 5。
前序遍历二叉树,输出结果。
中序遍历二叉树,输出结果。
后序遍历二叉树,输出结果。
return 0;:程序正常结束。【执行结果】输出结果将会是:
Preorder Traversal: 1 2 4 5 3 Inorder Traversal: 4 2 5 1 3 Postorder Traversal: 4 5 2 3 1
(6)应用举例
假设一棵二叉树的中序序列与后序序列分别为: B A C D E F G H 和 B C A E D G H F,建立该二叉树。

遍历二叉树的应用:
注:“遍历” 是二叉树各种操作的基础,可以在遍历过程中对结点进行各种操作,如:对于一棵已知二叉树
- 求二叉树中结点的个数
- 求二叉树中叶子结点的个数
- 求二叉树中度为 1 的结点个数
- 求二叉树中度为 2 的结点个数
- 求二叉树中非终端结点个数
- 交换结点左右孩子
- 判定结点所在层次
【示例 1】求二叉树中叶结点数目
【示例代码】编写求二叉树中叶结点个数的算法 (设二叉树的二叉链表的根指针为 bt ):
// 求二叉树中叶结点的数目 int leafcount(Bintree bt) {int n, m; // 声明变量n和m,用于存储左右子树的叶子数目if (bt == NULL) {return 0; // 空树没有叶结点,返回0}else if (bt->lchild == NULL && bt->rchild == NULL) {return 1; // 只有根节点的树,根节点即为叶结点,返回1}else {n = leafcount(bt->lchild); // 求左子树的叶子数目m = leafcount(bt->rchild); // 求右子树的叶子数目return (n + m); // 左子树叶子数目 + 右子树叶子数目} }【代码详解】
int leafcount(Bintree bt): 定义了一个名为leafcount的函数,参数类型为Bintree,返回值类型为int。
int n, m;: 声明了两个变量n和m,用于存储左子树和右子树的叶子数目。
if (bt == NULL) { ... }: 如果传入的二叉树为空,说明没有叶结点,直接返回0。
else if (bt->lchild == NULL && bt->rchild == NULL) { ... }: 如果二叉树只有根节点且没有左右子树,那么根节点就是叶结点,返回1。
else { ... }: 如果既不是空树,也不是只有根节点的情况,进入这个分支。
n = leafcount(bt->lchild);: 递归调用leafcount函数求左子树的叶子数目,并将结果存储到变量n中。
m = leafcount(bt->rchild);: 递归调用leafcount函数求右子树的叶子数目,并将结果存储到变量m中。
return (n + m);: 返回左子树的叶子数目加上右子树的叶子数目,即为整个二叉树的叶子数目。
- 这样,通过递归地遍历左右子树,可以得到整个二叉树的叶子数目。
【示例 2】在二叉树中找到度为 1 的结点,并输出它们的值,同时统计个数
【示例代码】编写输出二叉树中所有度为 1 的结点的数据域的值,并统计其数目的算法 (设二叉树的二叉链表的根指针为 t ):
// 输出二叉树t中度为1的结点值,并求其个数 int onesoncount(Bintree t) {if (t == NULL) {return 0; // 空树,度为1的结点个数为0}else {if ((t->lchild == NULL && t->rchild != NULL) ||(t->lchild != NULL && t->rchild == NULL)){printf(t->data); // 输出度为1的结点值return (onesoncount(t->lchild) + onesoncount(t->rchild) + 1); // 递归计算左右子树的度为1的结点个数,并加上当前结点}else {return (onesoncount(t->lchild) + onesoncount(t->rchild)); // 递归计算左右子树的度为1的结点个数之和}} }【代码详解】
int onesoncount(Bintree t): 定义了一个名为onesoncount的函数,参数类型为Bintree,返回值类型为int。如果二叉树
t为空,那么不存在度为1的结点,返回 0。如果二叉树
t的左子树为空,右子树不为空,或者左子树不为空,右子树为空,那么当前结点的度是 1,输出当前结点的值,并递归计算左子树和右子树的度为 1 的结点个数,并加上当前结点,返回结果。如果二叉树
t的左子树和右子树都不为空,那么当前结点的度不是 1,递归计算左子树和右子树的度为 1 的结点个数之和,并返回结果。
通过递归地遍历二叉树的左右子树,可以找到度为1的结点,并输出它们的值,同时统计个数。
最终,函数返回度为 1 的结点个数。
【示例 3】在二叉树中找到度为 2 的结点,并输出它们的数据域值,同时统计个数
【示例代码】编写输出二叉树中所有度为 2 的结点的数据域的值,并统计其数目的算法(设二叉树的二叉链表的根指针为 BT ):
// 输出二叉树BT中所有度为2的结点的数据域值,并统计其数目 int twoson(Bintree BT) {if (BT == NULL) {return 0; // 空树,没有度为2的结点,返回0}else if (BT->lchild == NULL || BT->rchild == NULL) {return (twoson(BT->lchild) + twoson(BT->rchild)); // 递归计算左右子树的度为2的结点数目之和}else if (BT->lchild != NULL && BT->rchild != NULL) {printf(BT->data); // 输出度为2的结点的数据域值return (twoson(BT->lchild) + twoson(BT->rchild) + 1); // 递归计算左右子树的度为2的结点数目之和,并加上当前结点} }【代码详解】
int twoson(Bintree BT): 定义了一个名为twoson的函数,参数类型为Bintree,返回值类型为int。如果二叉树
BT为空,那么不存在度为 2 的结点,返回 0。如果二叉树
BT的左子树为空或右子树为空,那么当前结点的度不是 2,递归计算左子树和右子树的度为 2 的结点数目之和,并返回结果。如果二叉树
BT的左子树和右子树都不为空,那么当前结点的度是 2,输出当前结点的数据域值,并递归计算左子树和右子树的度为 2 的结点数目之和,并加上当前结点,返回结果。
通过递归地遍历二叉树的左右子树,可以找到度为 2 的结点,并输出它们的数据域值,同时统计个数。
最终,函数返回度为 2 的结点个数。
【示例 4】在二叉树中找到非终端结点,并输出它们的值,同时统计个数
【示例代码】编写一算法,打印出一棵二叉树中所有非终端结点的值,并统计非终端结点的个数 (二叉树以二叉链表存储,根指针为 bt ):
// 求二叉树bt中非叶结点的数目 int notleafcount(Bintree bt) {if (bt == NULL) {return 0; // 空树,没有非叶结点,返回0}else if (bt->lchild == NULL && bt->rchild == NULL) {return 0; // 没有左右子树,也没有非叶结点,返回0}else {printf(bt->data); // 输出非终端结点的值n = notleafcount(bt->lchild); // 求左子树的非叶结点数目m = notleafcount(bt->rchild); // 求右子树的非叶结点数目return (m + n + 1); // 返回总的非叶结点数目} }【代码详解】
int notleafcount(Bintree bt): 定义了一个名为notleafcount的函数,参数类型为Bintree,返回值类型为int。如果二叉树
bt为空,那么没有非叶结点,返回 0。如果二叉树
bt既没有左子树也没有右子树,那么也没有非叶结点,返回 0。如果二叉树
bt既不是空树,也不是只有根节点的情况,进入这个分支。输出当前非终端结点的值。
递归调用
notleafcount函数求左子树的非叶结点数目,并将结果存储到变量n中。递归调用
notleafcount函数求右子树的非叶结点数目,并将结果存储到变量m中。返回左子树的非叶结点数目加上右子树的非叶结点数目加上当前非终端结点,作为总的非叶结点数目。
通过递归地遍历二叉树的左右子树,可以找到非终端结点,并输出它们的值,同时统计个数。
最终,函数返回非终端结点的数目。
【示例 5】统计二叉树中所有结点的个数
【示例代码】编写一算法,打印出一棵二叉树中所有结点的值,并统计结点的个数 (二叉树以二叉链表存储,根指针为 bt ) :
// 打印出二叉树t中所有结点的值,并统计结点的个数 int f5(Bintree bt) {if (bt == NULL) {return 0; // 空树,没有结点,返回0}else {printf(bt->data); // 输出结点的值n = f5(bt->lchild); // 求左子树的结点数目m = f5(bt->rchild); // 求右子树的结点数目return (m + n + 1); // 返回总的结点数目} }【代码详解】
int f5(Bintree bt): 定义了一个名为f5的函数,参数类型为Bintree,返回值类型为int。如果二叉树
bt为空,那么没有结点,返回 0。如果二叉树
bt不为空,进入这个分支。输出当前结点的值。
递归调用
f5函数求左子树的结点数目,并将结果存储到变量n中。递归调用
f5函数求右子树的结点数目,并将结果存储到变量m中。返回左子树的结点数目加上右子树的结点数目加上当前结点,作为总的结点数目。
通过递归地遍历二叉树的左右子树,可以打印出所有结点的值,并统计结点的个数。
最终,函数返回二叉树中所有结点的个数。
【示例 6】在二叉树中找到数据域值为 8 的结点,并统计个数
【示例代码】设二叉树存储结构采用二叉链表表示,每个结点的数据域中存放一个整数。试编写一个算法,求此二叉树上数据域的值为8的结点个数:
// 求二叉树bt结点数据域值为8的结点的数目 int f6(Bintree bt) {if (bt == NULL) {return 0; // 空树,没有结点,返回0}else if (bt->data == 8) {return (f6(bt->lchild) + f6(bt->rchild) + 1); // 数据域值等于8的结点数目加上左右子树的结点数目之和,加上当前结点}else {return (f6(bt->lchild) + f6(bt->rchild)); // 左右子树的结点数目之和} }【代码详解】
int f6(Bintree bt): 定义了一个名为f6的函数,参数类型为Bintree,返回值类型为int。如果二叉树
bt为空,那么没有结点,返回 0。如果二叉树
bt的数据域值等于 8,进入这个分支。返回数据域值等于 8 的结点数目加上左子树的结点数目加上右子树的结点数目,作为总的结点数目。
如果二叉树
bt的数据域值不等于 8,进入这个分支。返回左子树的结点数目加上右子树的结点数目,作为总的结点数目。
通过递归地遍历二叉树的左右子树,可以找到数据域值为 8 的结点,并统计个数。
最终,函数返回数据域值为 8 的结点的数目。
五、树和森林
(1)树的存储结构
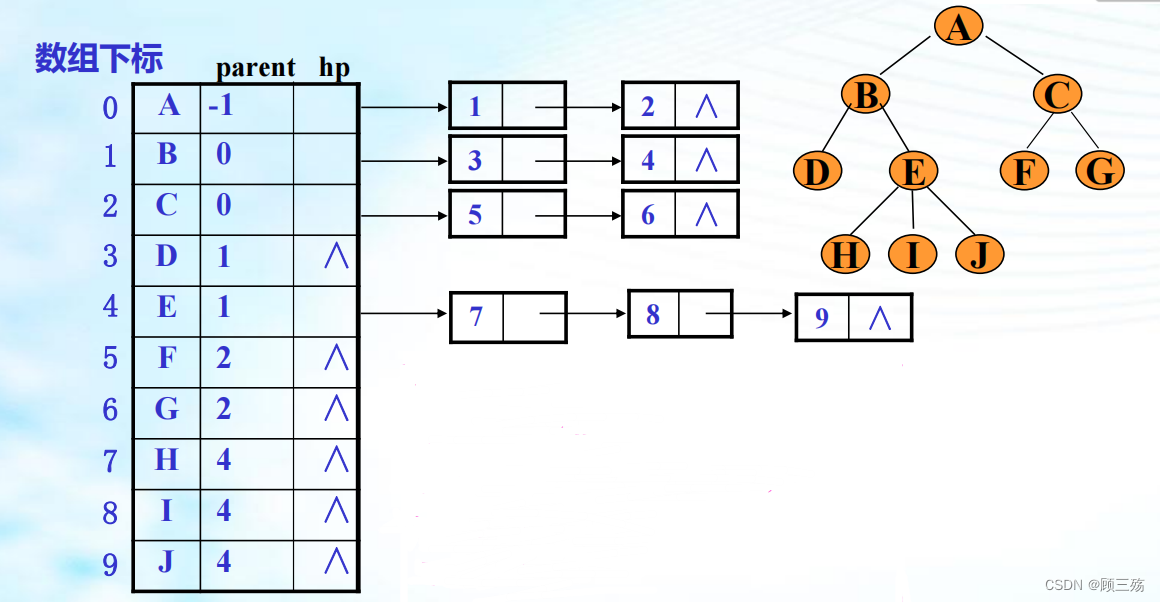
① 双亲表示法
- 以一组连续空间存储树的结点,即一个一维数组构成,数组每个分量包含两个域:数据域和双亲域。
- 数据域用于存储树上一个结点的数据元素值,双亲域用于存储本结点的双亲结点在数组中的序号(下标值)。
- 每个数组元素含两个成员, 即:(结点值和其双亲在表中的位置)
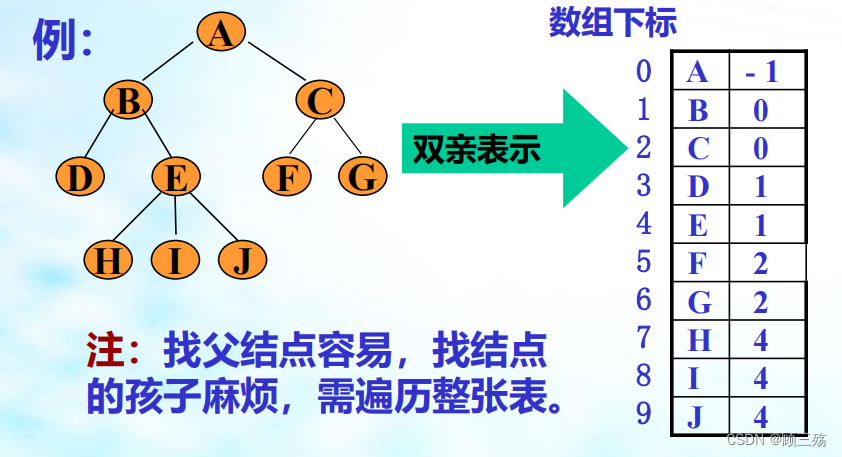
【说明】 根结点没有双亲,双亲域的值为 -1【类型定义】 双亲链表的类型定义如下:#define size 10typedef struct {datatype data; // 结点数据类型,假设为 datatypeint parent; // 结点的父节点 } Node;Node slist[size]; // 定义一个大小为 size 的 Node 数组,用于存储结点信息
#define size 10: 使用预处理指令#define定义一个名为size的符号常量,并将其值设置为 10。该符号常量可以在代码中代表常数值 10。
typedef struct { ... } Node;: 使用typedef关键字定义一个结构体类型,名为Node。该结构体中包含了datatype data和int parent两个成员变量。
datatype data;: 结构体中的成员变量data声明了一个名为data的变量,此处假设datatype是一种数据类型。
int parent;: 结构体中的成员变量parent声明了一个名为parent的变量,用于表示该结点的父节点。
Node slist[size];: 定义了一个大小为size的数组slist,数组中的元素类型为Node结构体。这个数组用于存储结点的信息,每个元素表示一个结点的数据域值和父节点的索引。
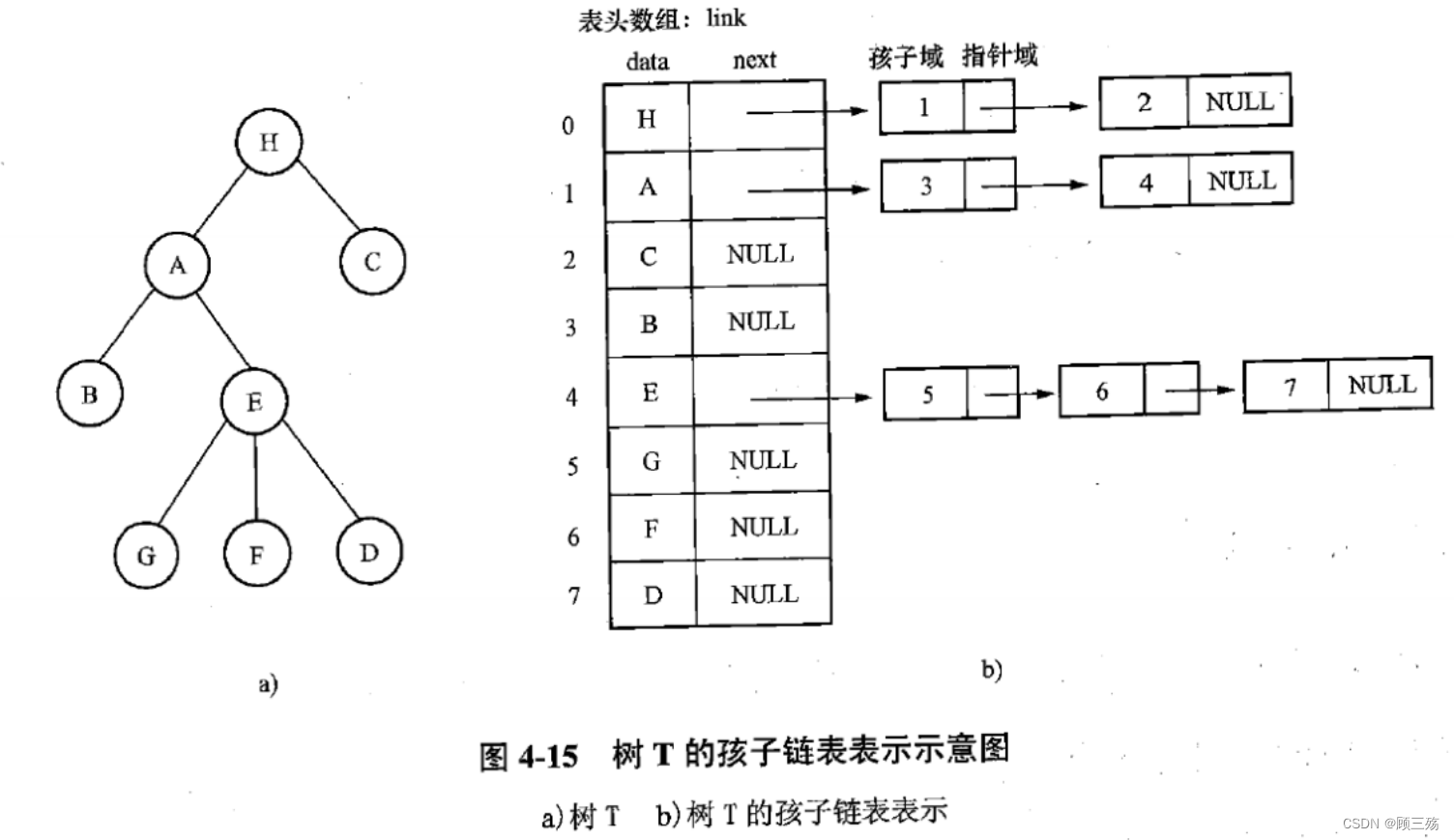
② 孩子链表表示法
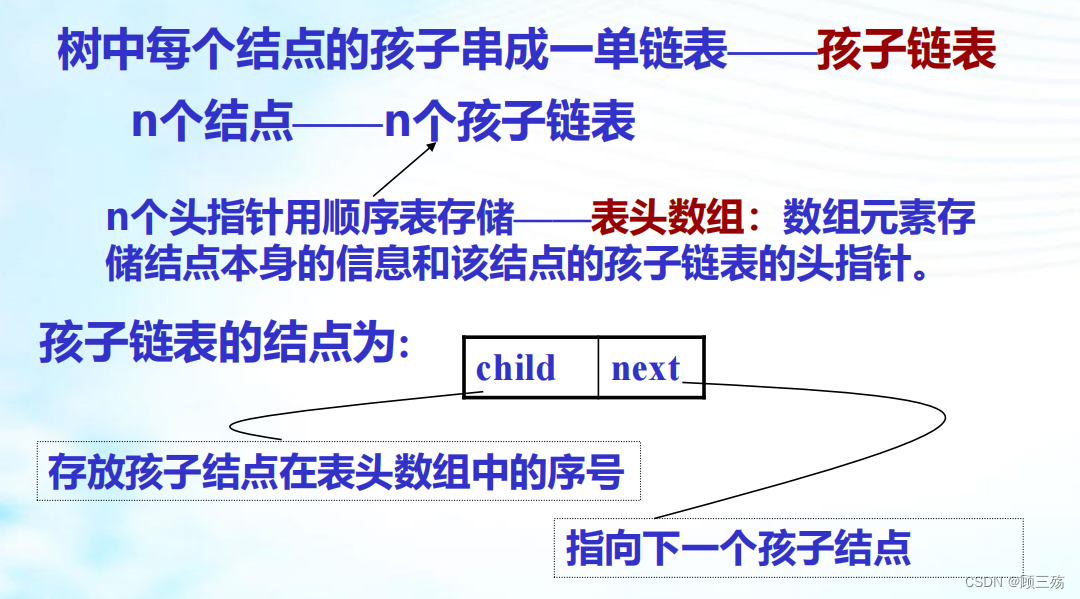
注: 在孩子链表表示中,找孩子方便,但求 结点的双亲困难,因此可在顺序表中再增加一个域,用于指明每个结点的双亲在表中位 置,即将双亲表示法和孩子链表表示法结合起来。
【类型定义】 孩子链表表示法的类型定义:#define MAXND 20typedef struct bnode {int child;struct bnode* next; } node, *childlink;typedef struct {DataType data;childlink hp; } headnode;headnode link[MAXND];
#define MAXND 20: 使用预处理指令#define定义一个名为MAXND的符号常量,并将其值设置为 20。该符号常量可以在代码中代表常数值 20。
typedef struct bnode { ... } node, *childlink;: 使用typedef关键字定义了一个结构体类型,名为bnode,结构体中包含了int child和struct bnode* next两个成员变量。同时也定义了两个别名node和childlink,node为结构体类型的别名,childlink为指向该结构体类型的指针类型的别名。
typedef struct { ... } headnode;: 使用typedef关键字定义了一个匿名结构体类型,名为headnode,结构体中包含了DataType data和childlink hp两个成员变量。
headnode link[MAXND];: 定义了一个名为link的数组,数组长度为MAXND,数组的元素类型为headnode结构体。数组中的每个元素表示一个头节点,包含了数据域和指向子节点的指针。
通过上述代码,定义了一种多叉树的表示方式。
link数组中的每个元素表示一个多叉树的头节点,该头节点包含了数据域和指向子节点的指针。
bnode结构体中的child成员表示子节点的索引,next成员表示指向下一个子节点的指针。
Ⅰ. 双亲孩子表示法
双亲孩子表示法:
- 树中每个结点的孩子串成一单链表 —— 孩子链表 n 个结点 —— n 个孩子链表
- 同时用一维数组顺序存储树中的各结点,数组元素除了包括结点本身的信息和该结点的孩子链表的头指针之外,还增设一个域,用来存储结点双亲结点在数组中的序号。
【类型定义】双亲孩子表示法的类型定义:
#define MAXND 20typedef struct bnode {int child;struct bnode* next; } node, *childlink;typedef struct {DataType data;int parent;childlink hp; } headnode;headnode link[MAXND];
#define MAXND 20: 使用预处理指令#define定义一个名为MAXND的符号常量,并将其值设置为 20。该符号常量可以在代码中代表常数值 20。
typedef struct bnode { ... } node, *childlink;: 使用typedef关键字定义了一个结构体类型,名为bnode,结构体中包含了int child和struct bnode* next两个成员变量。同时也定义了两个别名node和childlink,node为结构体类型的别名,childlink为指向该结构体类型的指针类型的别名。
typedef struct { ... } headnode;: 使用typedef关键字定义了一个匿名结构体类型,名为headnode,结构体中包含了DataType data、int parent和childlink hp三个成员变量。
headnode link[MAXND];: 定义了一个名为link的数组,数组长度为MAXND,数组的元素类型为headnode结构体。数组中的每个元素表示一个头节点,包含了数据域、父节点和指向子节点的指针。
通过上述代码,定义了一种多叉树的表示方式。
link数组中的每个元素表示一个多叉树的头节点,该头节点包含了数据域、父节点和指向子节点的指针。
bnode结构体中的child成员表示子节点的索引,next成员表示指向下一个子节点的指针。
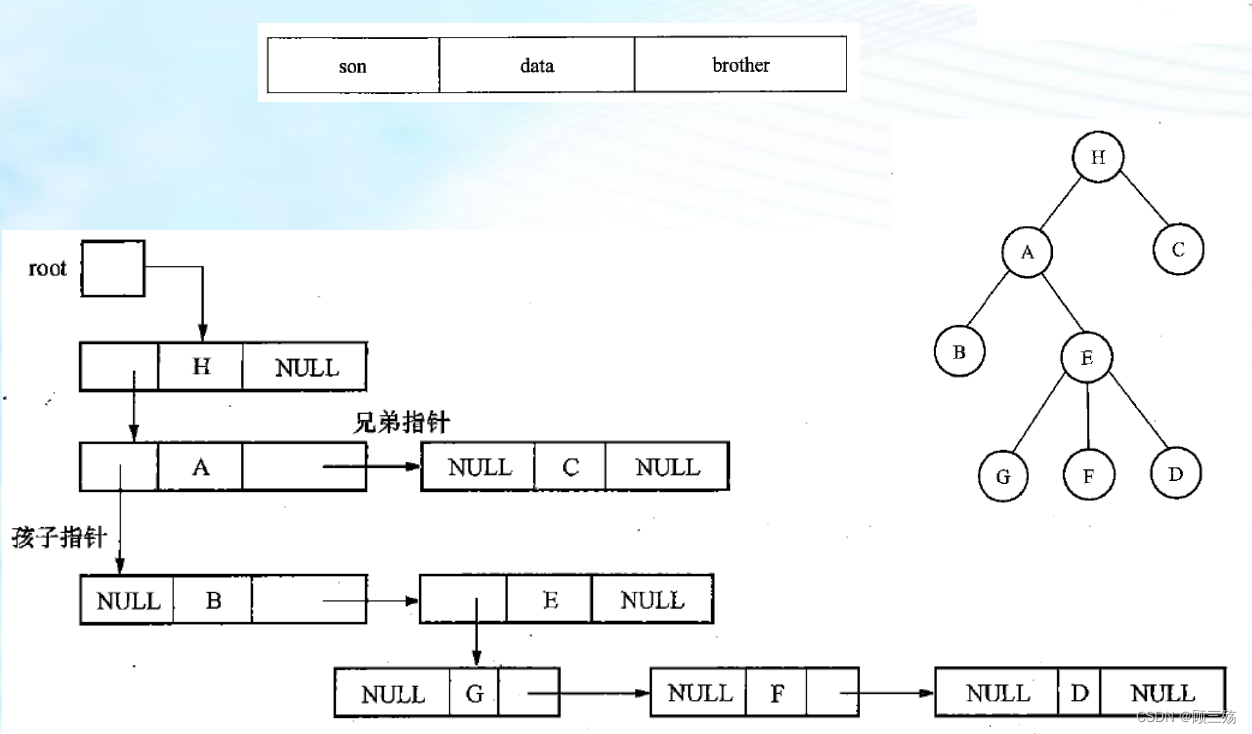
③ 孩子兄弟链表表示法(二叉链表表示)
孩子兄弟链表 的结构形式与 二叉链表 完全相同,但结点中指针的含义不同。
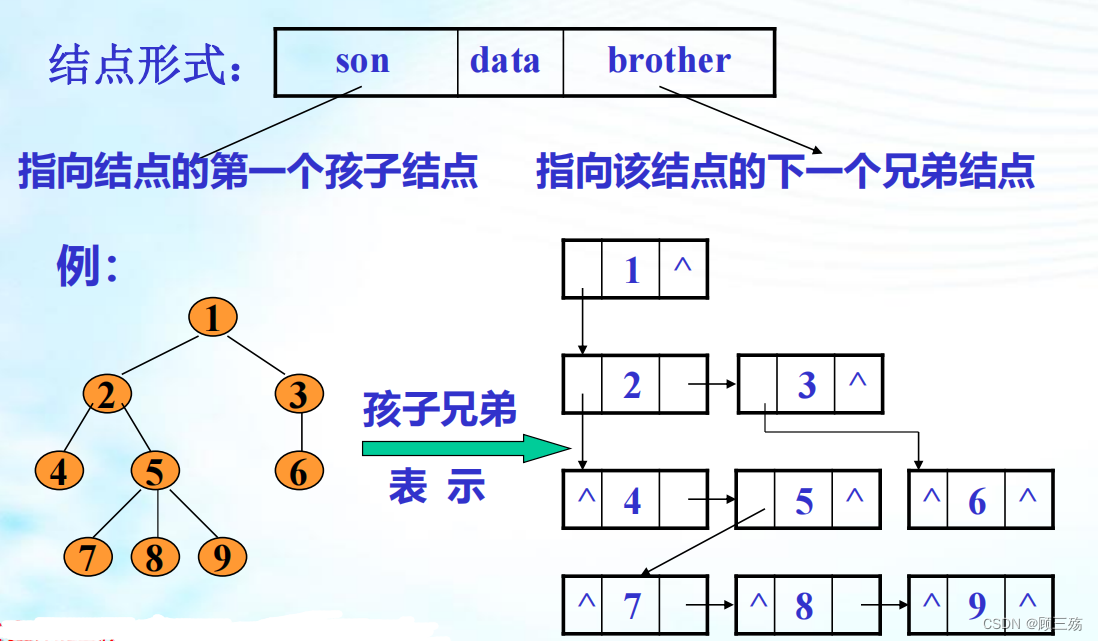
【类型定义】 孩子兄弟链表表示法的类型定义:typedef struct tnode {DataType data;struct tnode* son; // 指向第一个子节点的指针struct tnode* brother; // 指向下一个兄弟节点的指针 } *Tree;
typedef struct tnode { ... } *Tree;:使用typedef关键字定义了一个结构体类型,名为tnode。结构体中包含了DataType data、struct tnode* son和struct tnode* brother三个成员变量。同时,通过*Tree的方式定义了指向该结构体类型的指针类型别名。
DataType data;:结构体中的成员变量data声明了一个名为data的变量,用于存储结点的数据。
struct tnode* son;:结构体中的成员变量son声明了一个名为son的指针变量,该指针指向当前结点的第一个子节点。
struct tnode* brother;:结构体中的成员变量brother声明了一个名为brother的指针变量,该指针指向当前结点的下一个兄弟节点。
*Tree:通过*Tree的方式定义了指向该结构体类型的指针类型别名。这样,以后我们可以使用Tree来声明指向tnode结构体类型的指针。
通过上述代码,定义了一种树的表示方式。
tnode结构体中的son成员指向当前结点的第一个子节点,brother成员指向当前结点的下一个兄弟节点。通过使用
*Tree作为指向tnode结构体类型的指针类型别名,可以声明树的节点指针变量。


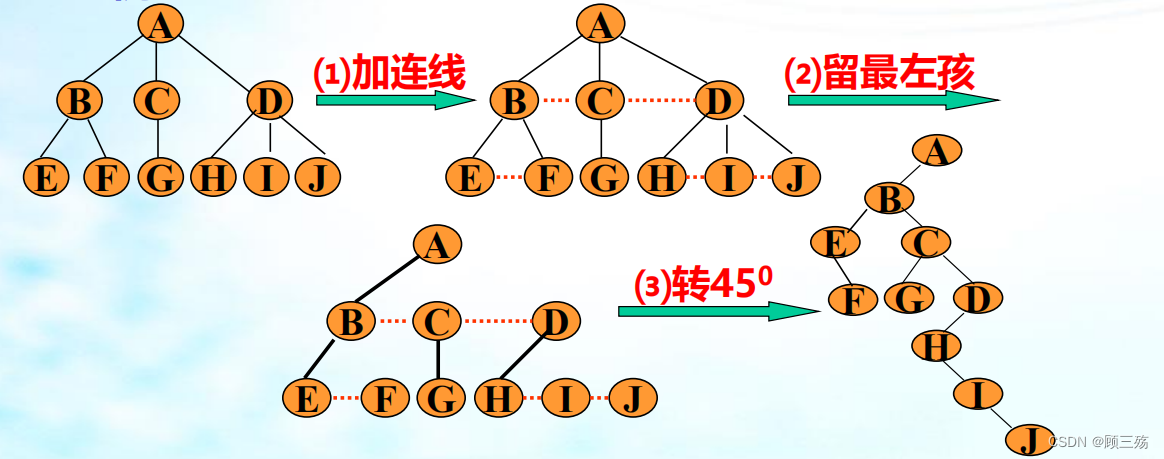
(2)树、森林与二叉树的关系
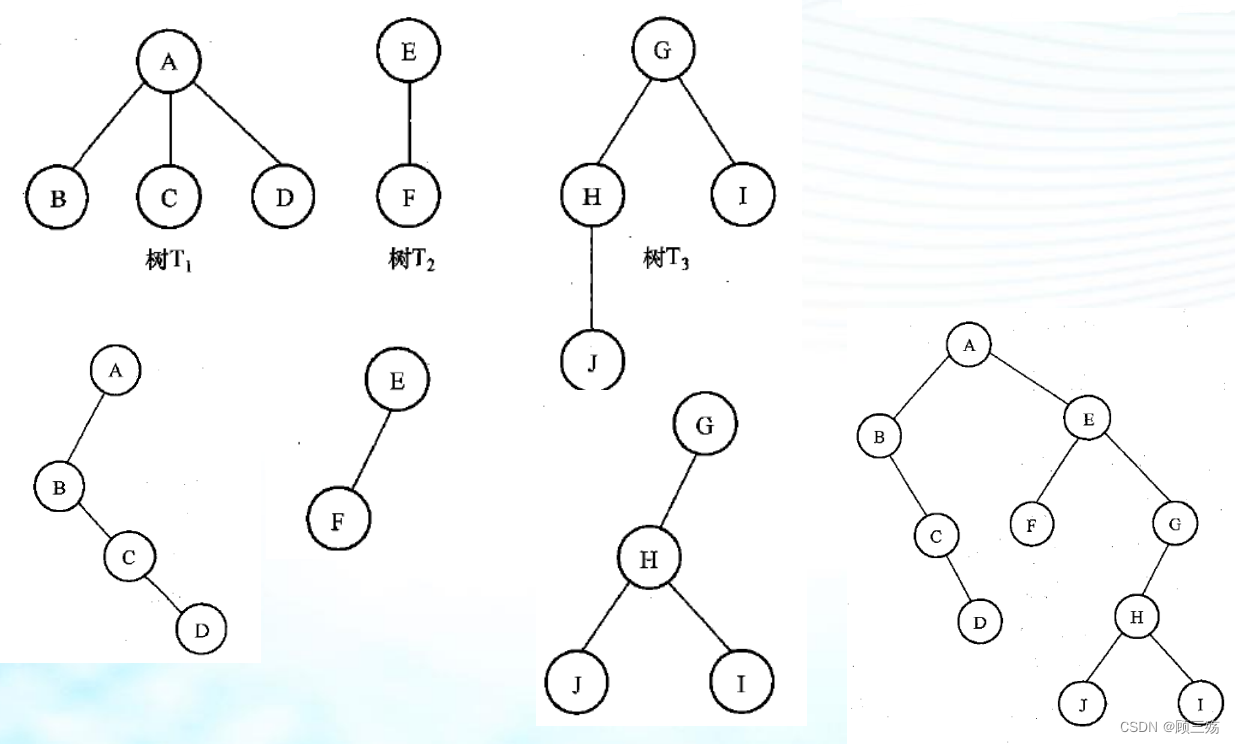
① 一般树 → 二叉树
方法:
- 各兄弟之间加连线
- 对任一结点,除最左孩子外,抹掉该结点与其余孩子的各枝
- 以根为轴心,将连线顺时针转 450°
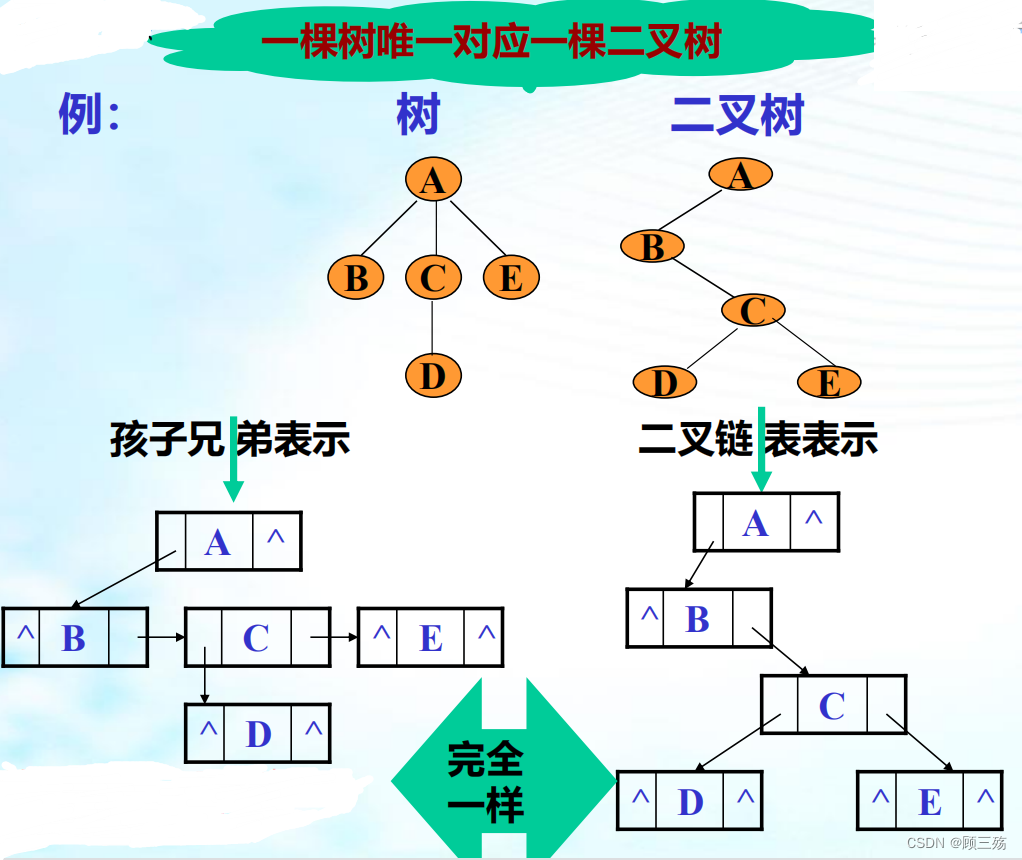
孩子兄弟链表 的结构形式与二叉链表完全相同,但结点中指针的含义不同。
② 森林 → 二叉树
森林 F 转换成二叉树的方法如下:
- 将每棵树转换成相应的二叉树
- 将第 1 点中得到的各棵二叉树的根结点看做是兄弟连接起来
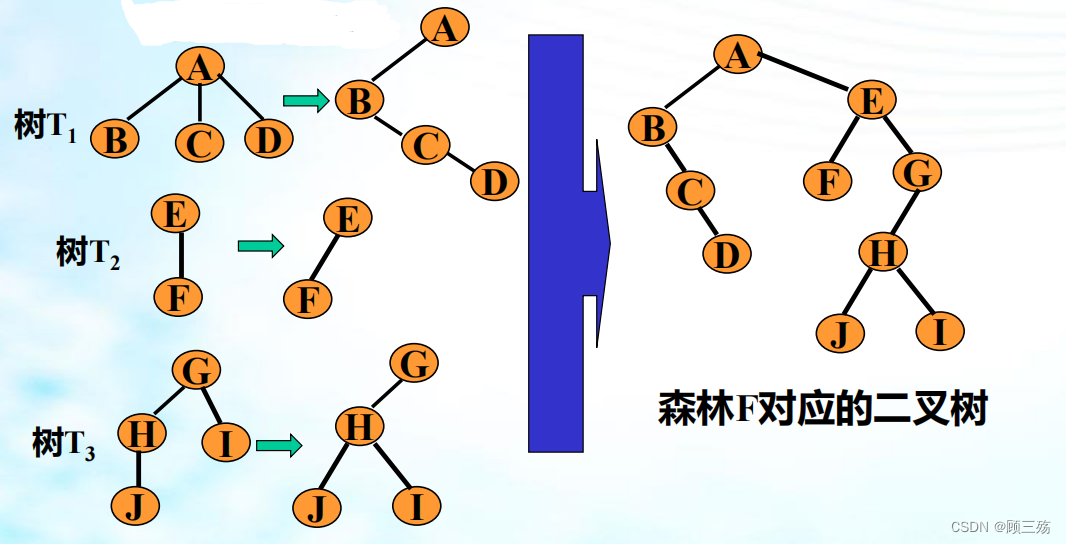
③ 二叉树 → 一般树
 方法:
方法:
- 从根结点起
- 该结点左孩和左孩右枝上的结点依次作为该结点孩子
- 重复第 1 点
- 根无右孩的二叉树可以转变成一般树

(3)树和森林的遍历
① 树的遍历
- 先序遍历:先访问根结点,然后依次先序遍历根的每棵子树
- 后序遍历:先依次后序遍历每棵子树,最后访问根结点
- 层次遍历:
② 森林的遍历
⚫ 先序 遍历森林 : 访问森林中每棵树的根结点;先序遍历森 林中第一棵树的根结点的子树组成的森林;先序遍历除去 第一棵树之外其余的树组成的森林
- 对下图中森林进行先序遍历的序列为: A B C D E F G H J I
⚫ 中序 遍历森林 : 中序访问森林中第一棵树的根结点的子树 组成的森林;访问第一棵树的根结点;中序遍历除去第一 棵树之外其余的树组成的森林
- 对下图中森林进行先序遍历的序列为: B C D A F E J H I G

六、判定树和哈夫曼树
(1)分类与判定树
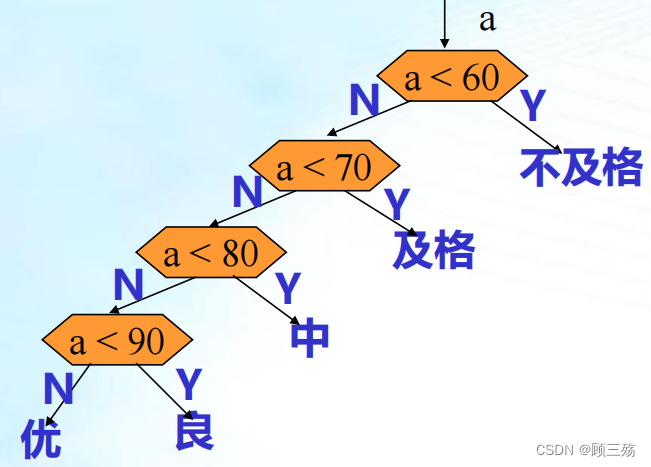
【问题】n 个学生成绩 a1,a2,…,an (百分制),现要转换成五分制,即 a1,a2,…,an 分五类:
- 一类:< 60 不及格
- 二类:[ 60, 70 ) 及格
- 三类:[ 70, 80 ) 中等
- 四类:[ 80, 90 ) 良好
- 五类:≥ 90 优秀

【若按顺序判,得下列判断过程】
判定树 : 用于描 述分类过程的二叉 树,其中:每个非 终端结点包含一个 条件,对应一次比较;每个终端结点 包含一个种类标记, 对应于一种分类结 果。
- 对 n 个数分类花费时间较多。
- 因为大多数元素属于中和良,这样大多数数据都得通过 3 至 4 次判断,这样总的判断次数就多。

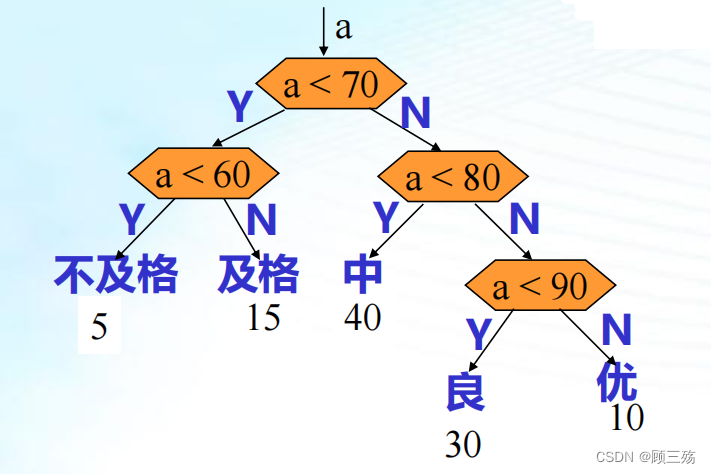
- 总的判断次数最少。
- 因为属于中、良的数最多,而检验它们的判断少,因此总的判断次数少。

(2)哈夫曼树与哈夫曼算法
① 路径长度
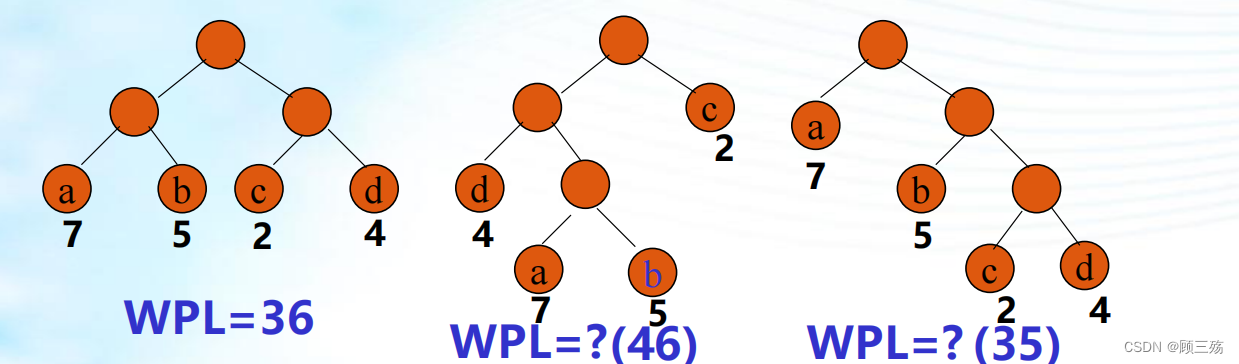
- 叶结点带权的二叉树:
- 结点 ni 的带权路径长度:
- 叶结点带权的二叉树路径长度 WPL:

② 哈夫曼树
【示例】二叉树有 4 个叶子,权分别为 7,5,2,4
【结论】
③ 哈夫曼算法
【方法】

【示例】
【说明】采用顺序存储,设置大小为 2n-1 的数组,每个数组元素由 4 个域组成:
- 存储权值、双亲指针、左孩子指针和右孩子指针
【类型定义】类型定义如下:
const int n = 10;typedef struct {float w; // 结点的权值int parent, lchild, rchild; // 父结点和左、右孩子所在数组的下标 } node;typedef node hftree[2 * n - 1]; // 使用 typedef 定义了一个名为 hftree 的数组类型,数组大小为 2 * n - 1,元素类型为 node 结构体
const int n = 10;: 使用 const 关键字定义了一个名为 n 的整型常量,并将其值设置为 10。这个常量 n 的值是不可修改的。
typedef struct { ... } node;: 使用 typedef 关键字定义了一个结构体类型,名为 node。结构体中包含了 float 类型的 w,int 类型的 parent、lchild 和 rchild 四个成员变量。
float w;: 结构体中的成员变量 w 声明了一个名为 w 的变量,用于存储结点的权值。
int parent, lchild, rchild;: 结构体中的成员变量 parent、lchild 和 rchild 声明了三个名为 parent、lchild 和 rchild 的整数变量,分别表示父结点和左、右孩子在数组中的下标。
typedef node hftree[2 * n - 1];: 使用 typedef 关键字定义了一个名为 hftree 的数组类型,数组大小为 2 * n - 1。元素类型为 node 结构体,即数组的每个元素都是一个 node 类型的结构体对象。
通过上述代码,定义了一个名为 hftree 的数组类型,用于存储哈夫曼树的结点信息。
数组的大小为 2 * n - 1,其中 n 是一个常量。
每个数组元素都是一个 node 结构体对象,包含了权值、父结点和左右孩子的下标信息。
哈夫曼算法:
1. 将表示哈夫曼树的数组T中的 2n-1 结点初始化;2. 读入 n 个权值到数组 T 的前 n 个分量中,它们是初始森林中的 n 个孤立的根结点的权值;3. 对森林中的树进行 n-1 次合并,共产生 n-1 个新结点,依次放入数组 T 的第 i 个分量重(n<=i<2*n-1)。每次合并的步骤如下:
- 从当前森林的所有结点 T[j](0<=j<=i-1) 中选取具有最小权值和次小权值的两个根结点,分别用 x 和 y 记住这两个根结点在数组 T 中的下标。
- 将根为 T[x] 和 T[y] 的两棵树合并,使它们分别成为新结点 T[i] 的左右孩子,得到一棵以新结点 T[i] 为根的二叉树。同时修改 T[x] 和 T[y] 的双亲域 parent,使其指向新结点 T[i],将T[x] 和 T[y] 的权值相加后作为新结点 T[i] 的权值。
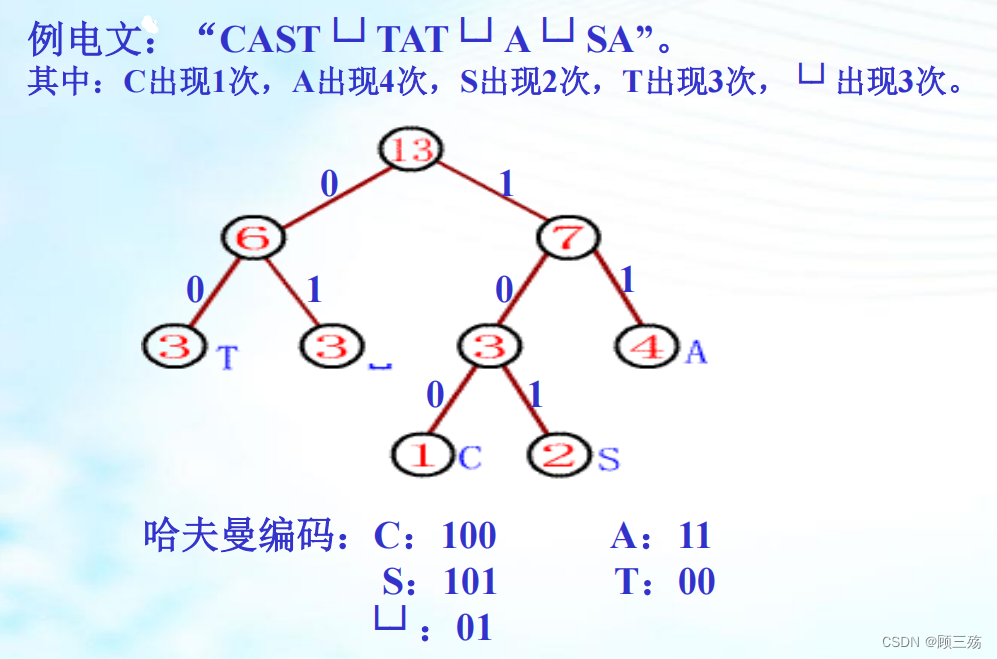
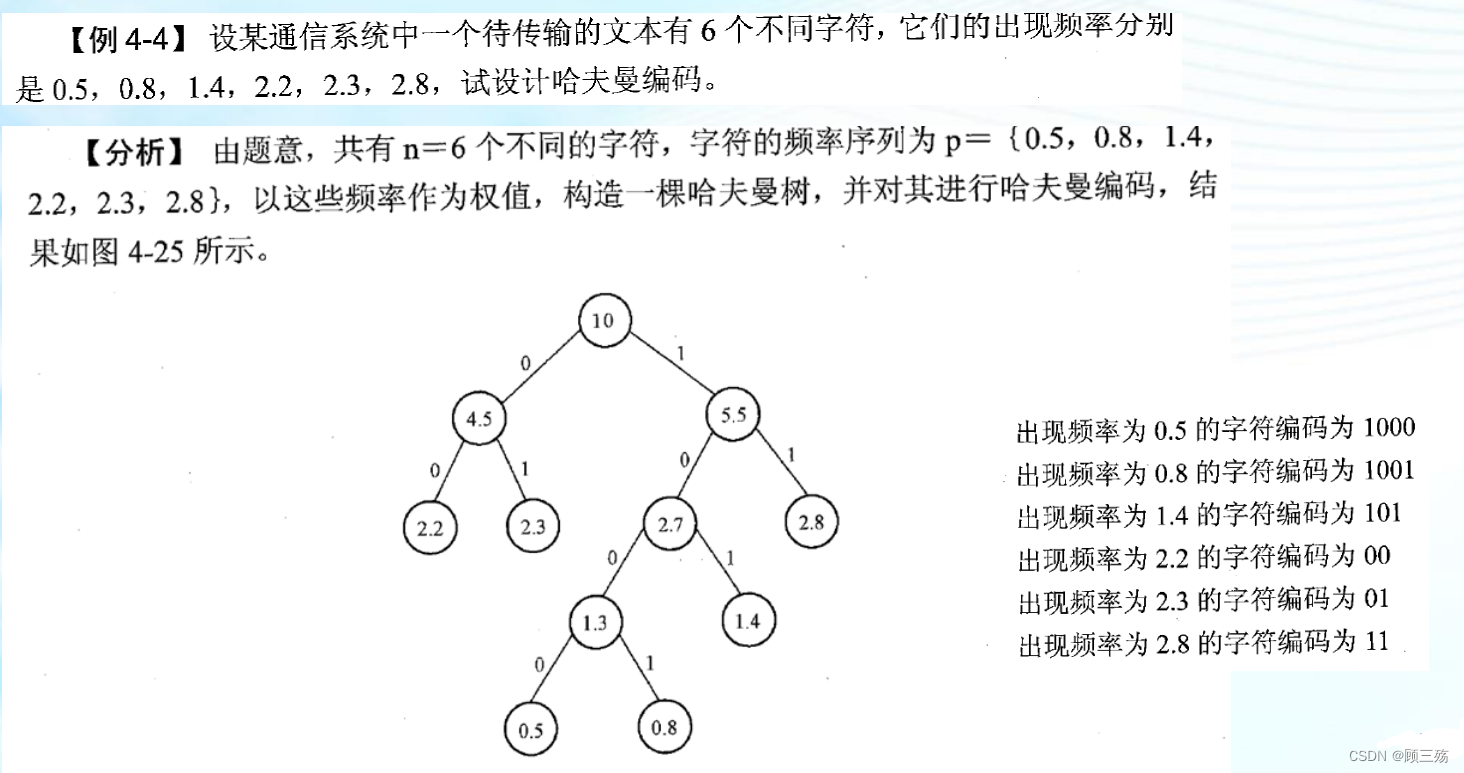
④ 哈夫曼编码

哈夫曼编码:
- 可利用哈夫曼树构造用于通信的二进制编码称为哈夫曼编码。
- 树中从根到每个叶子都有一条路径,对路径上的各分支约定指向左子树根的分支表示 “0” 码,指向右子树的分支表示 “1” 码,取每条路径上的 “0” 或 “1” 的序列作为和各个叶子对应的字符的编码,这就是哈夫曼编码。
哈夫曼编码的应用: