我是荔园微风，作为一名在IT界整整25年的老兵，今天总结一下Windows系统数据结构——最小生成树、Prim算法和Kruskal算法。

我在各在论坛看了很多相关帖子，发现一个简单的问题都被复杂化了。最小生成树、Prim算法和Kruskal算法真的没有大家想的那么复杂。

一些所谓的数据结构教材把这个问题讲的极其复杂，其实这真的没有必要。其实这个问题只需要两张图就可以全部搞懂。

我们下面来看看这个问题。

最小生成树的基本概念

最小生成树： 在一个连通网的所有生成树中，各边的代价之和最小的那棵生成树称为该连通网的最小代价生成树, 简称为最小生成树。
Prim算法和Kruskal算法是两个利用最小生成树性质构造最小生成树的算法

如果连通图的子图是一棵包含该图所有顶点的树，则该子图称为连通图的生成树。生成树往往不唯一。Prim算法和Kruskal算法是求连通带权无向图的最小生成树的常用算法。两种算法都采用贪心策略。

1.Prim算法

Prim算法的实现原理
假设图中的所有顶点和边结点存于U全集集合中，而新建一个集合T用于存放最小生成树的结点。从U集合中的某个顶点开始，不断查找到U-V集合的最小权值边和边所依附的另一个顶点，将此最小权值边和另一个顶点归并入T集合中，在实行完归并操作后，检查此时U-V中的所有结点到刚归入的结点的边的权值是否有小于当前辅助数组单元值lowcost值的情况，若有此情况，则更新辅助数组单元值，使辅助数组的lowcost中永远存放剩余顶点到T集合的最小边权值。
 

设一个带权连通无向图为G=(V,E),其中顶点集合V有n个顶点。
(1)设置一个顶点集合U和边集合T,U的初始状态为空。
(2)选定一条最小权值的边，并将顶点加入到顶点集合U中。
(3)重复下面的步骤，直到集合U=V为止：
1)选择一条最小权值的边(i,j),且满足i∈U,j∈V-U。
2)把顶点j加到顶点集合U中，把边(i,j)加到边集合T中。
此时，T为图G的最小生成树。如下图。

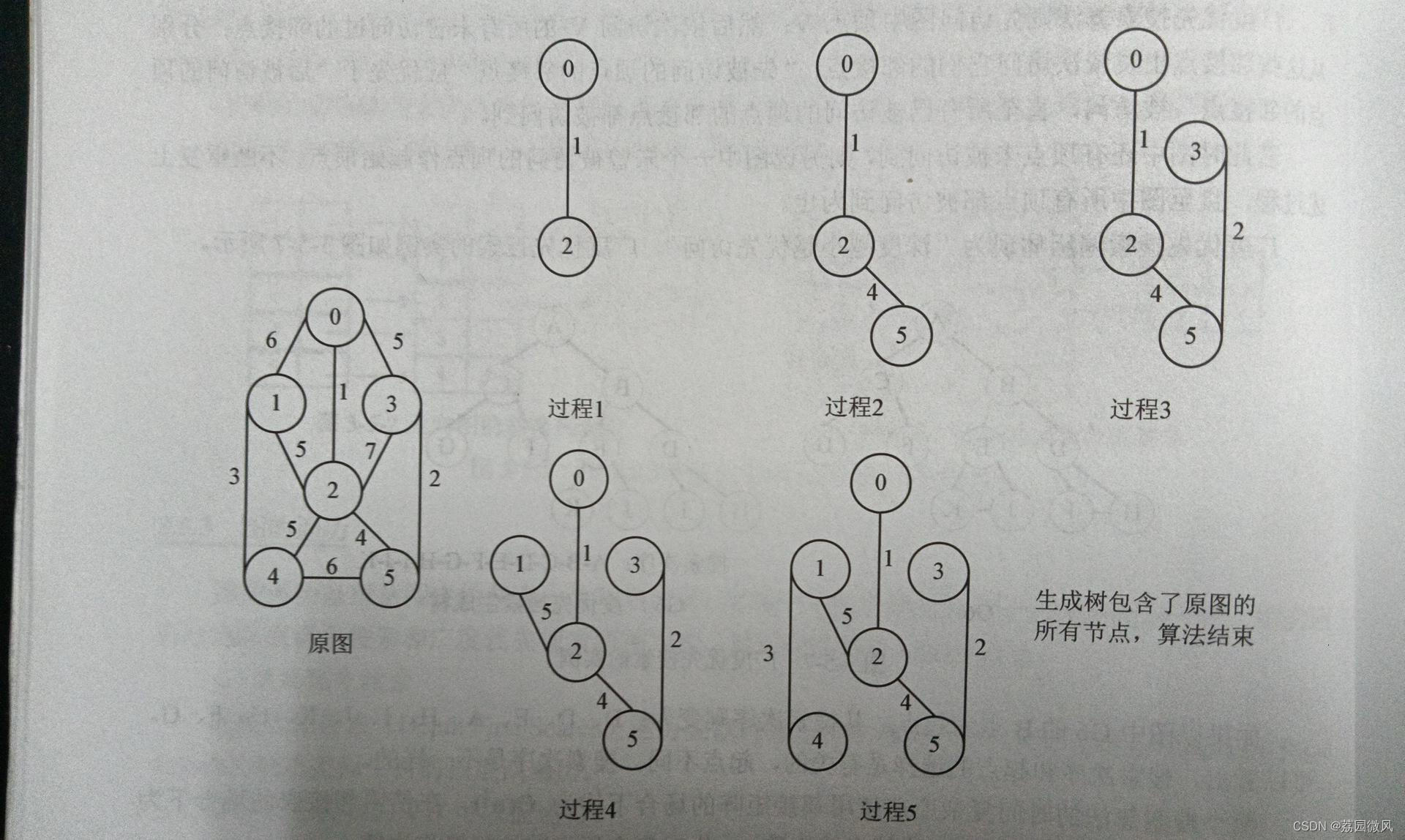
 该算法的时间复杂度为O(n^2)，只和顶点相关，适合于稠密图。

2.Kruskal算法

Kruskal算法的实现原理
设置两个辅助数组Edge和Vexset，Edge用来存储边权值及边依附的始点和终点，Vexset用来存储各顶点的连通分量值（Vexset的单元值相同则表明顶点属于同一个连通分量）。根据输入的边数和点数创建无向图的邻接矩阵，此处不同的是，需要将输入的边信息存储到辅助数组Edge中去。将Edge数组中的元素按边权值从小到大排序，初始化Vexset数组。按照边权值从小到大的顺序，依次使边依附的终点和始点属于同一个连通分量，直到遍历结束边信息，此时最小生成树的所有结点同属于一个连通分量，最小生成树构造完毕。
 

设初始状态只有n个顶点且无边的森林T，选择最小代价的边加入T，直到所有顶点在同一连通分量上，这就生成了最小生成树。这里加入边应避免环的出现。如图所示。

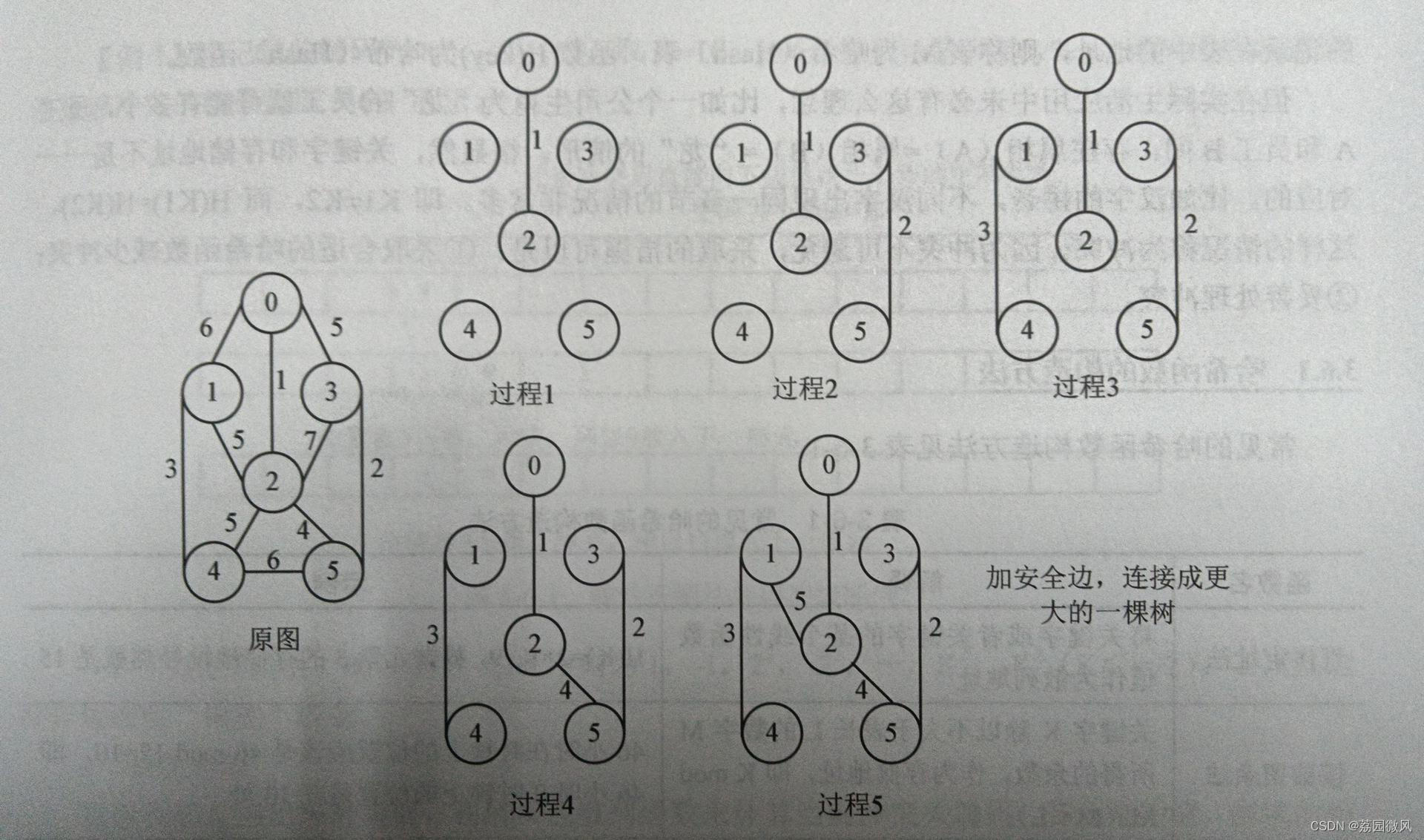
  该算法的时间复杂度为O(elog2e)，只和边相关，较适合于稀疏图。

作者简介：荔园微风，1981年生，高级工程师，浙大工学硕士，软件工程项目主管，做过程序员、软件设计师、系统架构师，早期的Windows程序员，Visual Studio忠实用户，C/C++使用者，是一位在计算机界学习、拼搏、奋斗了25年的老将，经历了UNIX时代、桌面WIN32时代、Web应用时代、云计算时代、手机安卓时代、大数据时代、ICT时代、AI深度学习时代、智能机器时代，我不知道未来还会有什么时代，只记得这一路走来，充满着艰辛与收获，愿同大家一起走下去，充满希望的走下去。