01、开篇语

各位小伙伴，你们好。

本期与您介绍AIAG MSA手册中对线性分析的推荐方法（就称作回归法吧）。通常情况下，偏倚和线性分析是同时进行的，原因在于线性分析是分析偏倚在量具的量程范围内的表现，可包含某具体测量值的偏倚。比如数显卡尺的工作标称范围是0-25cm，企业可能会应用 5、10、15、20几个测量点，此时会考虑各点偏倚以及线性的变差情况。前面文章已对“偏倚”研究做了两种方法的介绍，本期对线性分析的学习过程做概括性介绍。

02、MSA线性相关概念

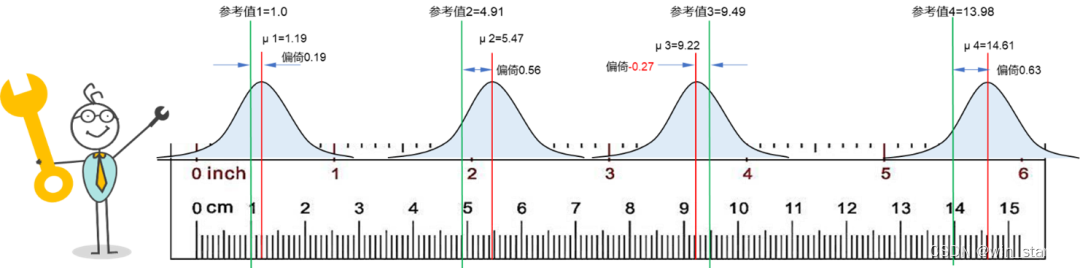
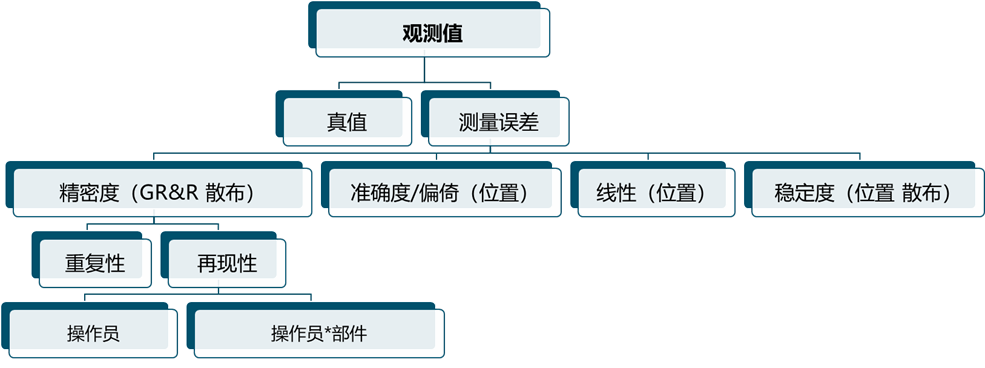
1. 如图所示，“线性”是偏倚在工作范围内或标称范围内的变化；

2. 这里请朋友注意一下MSA手册中关于“线性”术语的介绍：

在第一章 A节 术语汇总中，“线性”包括3个解释：

- 在量具正常工作量程内的偏倚变化量

- 在多个独立的偏倚误差在量具工作量程内的关系

- 是测量系统的系统误差所构成

在附录“术语”部分，“线性”解释如下：

线性：量具在预期工作范围内偏倚的差值。换句话说，线性是多个且独立的偏倚误差在整个量具的工作行程内的相关性。

【注意】“工作量程”（如使用20、40、60、80、100mm构成预期工作范围20-100mm）与“标称量程”（如0-250mm-量具实际刻度）的不同；通常以实际的应用为准（即研究目标的范围≤标称量程），并非所有的测量点均进行分析（同时也是成本的考虑）。

03、请了解“回归法”的概念

1. 线性研究的原理方法，通常是一元线性回归法。找几个比较有代表性的点进行偏倚分析，然后回归分析对各点的偏倚进行拟合形成一个 y=ax+b的一元回归方程（线性拟合 – 评价拟合优度r²）；

2. 拟合优度r²（相关系数r的平方），是z值法的典型应用；

​3. z值的意思是“测量个体和均值之间相差了几个标准差就是标准值，即z值。z值=(具体的数值减去均值)/这组数的标准差；

​以示例来说明，假设以下几个自然数：

 4. 相关系数（也称皮尔逊相关系数），是评价两个变量之间相关性强度的度量，基础公式为：

 以“身高、体重”的示例来说明r的计算（拆解为z值计算过渡）：

 身高和体重之间的相关系数r=((-0.5×-0.6）+0×(-1.0) + (-0.3)×(-0.2)+ …+ (-1.6)×(-0.6)) /(9-1) =0.73972

5. 了解以上这些基础知识将为后续步骤的学习做铺垫。

04、线性研究的操作步骤

同其他方法一样，AIAG-MSA手册给出的指南仅是概括性介绍，将操作方法推给专业的统计软件，本文对线性研究过程起到辅助作用。

【步骤1】MSA计划

同偏倚研究一样，将研究对象纳入MSA计划，一系列的策划活动在此不多赘述。

【步骤2】选定样品/建立基准

如指南中所述，存在过程变差，依据实际的量具使用范围，选择测量点：

- 识别和确定预期的工作范围

- 工程师选件，如2、4、6、8、10mm，即选定样件数为5个（用g表示）

- 对零件多次精密测量求平均值，填入下述表格相应栏目

 备注：场景及数据是模拟的，仅为学习而设，可以以您自己的实际数据为准。

【步骤3】选定人员和设备

- 1名固定的操作工或检验员 即k=1；（如果有多名操作工/检验员使用该测量设备，就是多次分析）

- 他/她使用的卡尺（需经过常规校准）

​【步骤4】测量、记录、初步计算

​计量工程师在策划时，要求选定的人员对每个零件至少测量10次以上（用m表示），此处测量m=12次

- 操作工/检验员对每个零件的测量点进行测量，可以间隔一定的时间，比如每2分钟（计量工程师要注意：盲测）

- 每个件测量12次

- 数据填入表格

 - 计算偏倚，如下：

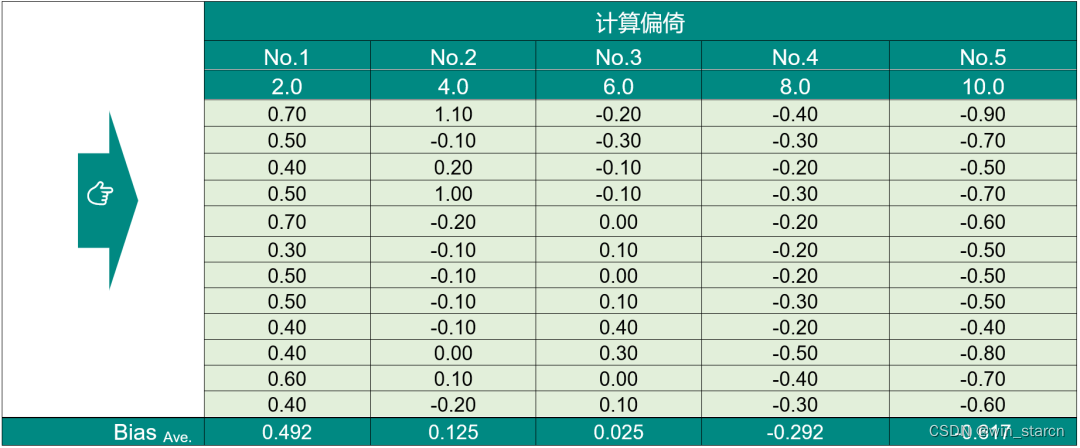
 偏倚值 = 测量值-基准值（这个概念始终要记得）

【步骤5】开始一系列复杂计算，建议使用Excel处理

- 该计算过程相对还是非常复杂的，要逐一摸索

- 为了呈现直观性，见下述表格

上述表格中蓝色的字体是Excel函数，在这里起到意想不到的作用（应当要掌握）。

计算过程需要特别的耐心。提示如下：

- 同样需要学习和了解假设检验（t检验）的知识

- 表中7第和8、11中yi代表每组的偏倚均值，xi表示每个基准值

- 表中第9项选择各组偏倚均值

- 第12项的计算，用SUMPRODUCT（偏倚数据区，基准值辅助区域），这样建立辅助区

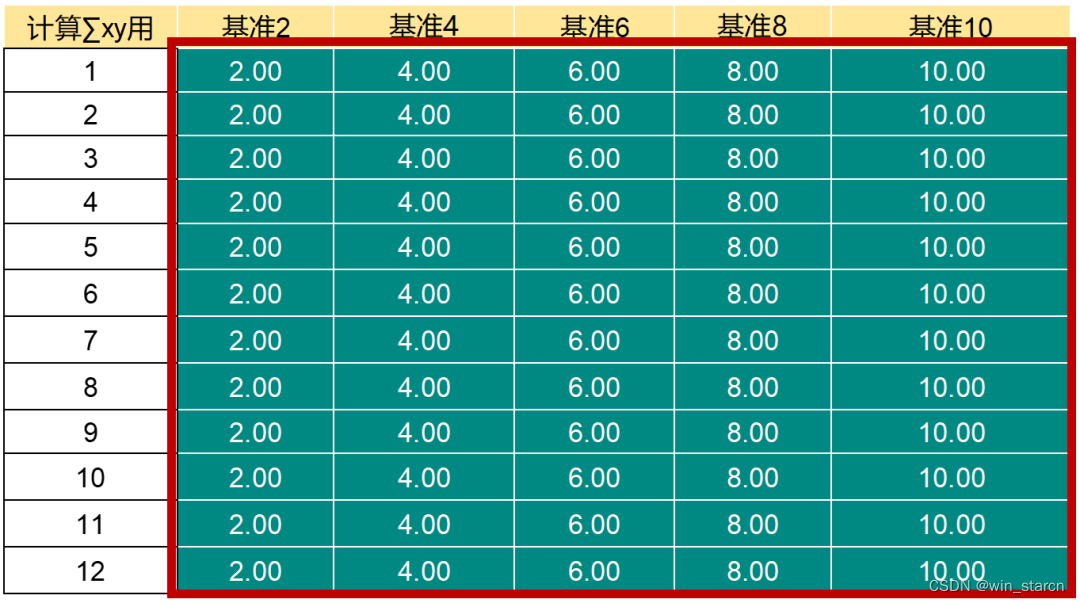
- 第19项中，| a | 读作a的绝对值，函数是ABS(具体数值)

【步骤6】分析准备

分析前要做的准备：

-σ重复性与过程变差或公差进行比较，判断是否满足条件（即<10%满足条件，可以进行后续的分析），本例中就假设与过程变差进行比较。

1) 这里的σ重复性=S=0.23954

​2) 用STDEV.P (原始测量值) 估算一下总体标准差=2.46≈2.5（很巧，跟手册差不多）

​3) 进行比较 0.2395/2.5≈9.6% < 10%，满足条件，可以继续分析

-构建一下方程 y = ax +b = - 0.13167*X + 0.73667（后续作线性拟合图添加线性趋势线，就应该得出同样的这个公式）

-对各组偏倚的置信区间画出拟合图（得有个辅助数据区域，这样建立）

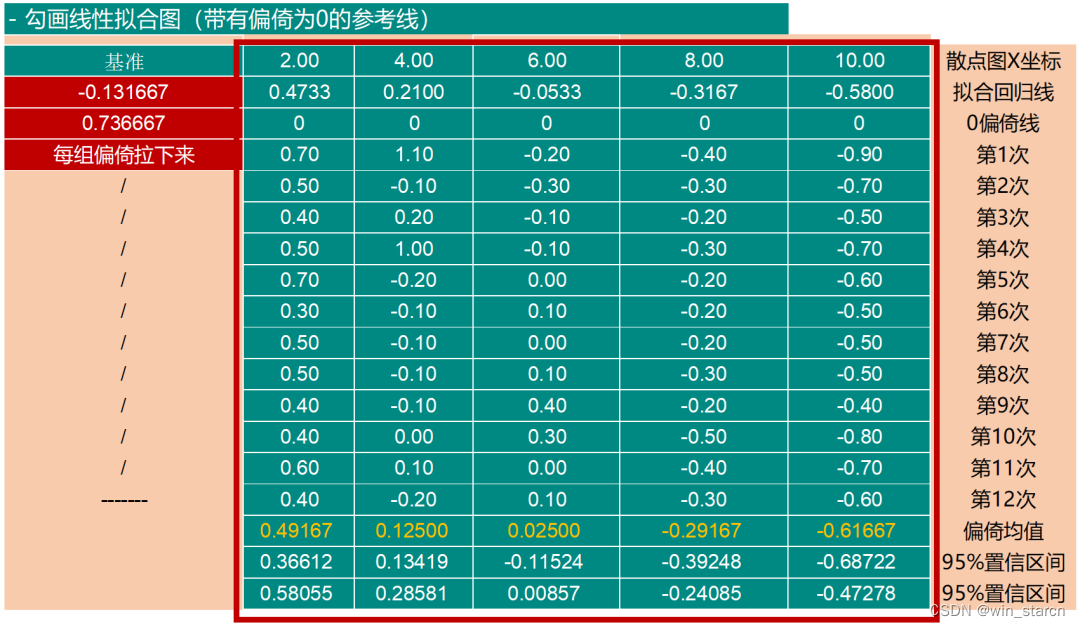
 95%置信区间计算为：

 成图如下：

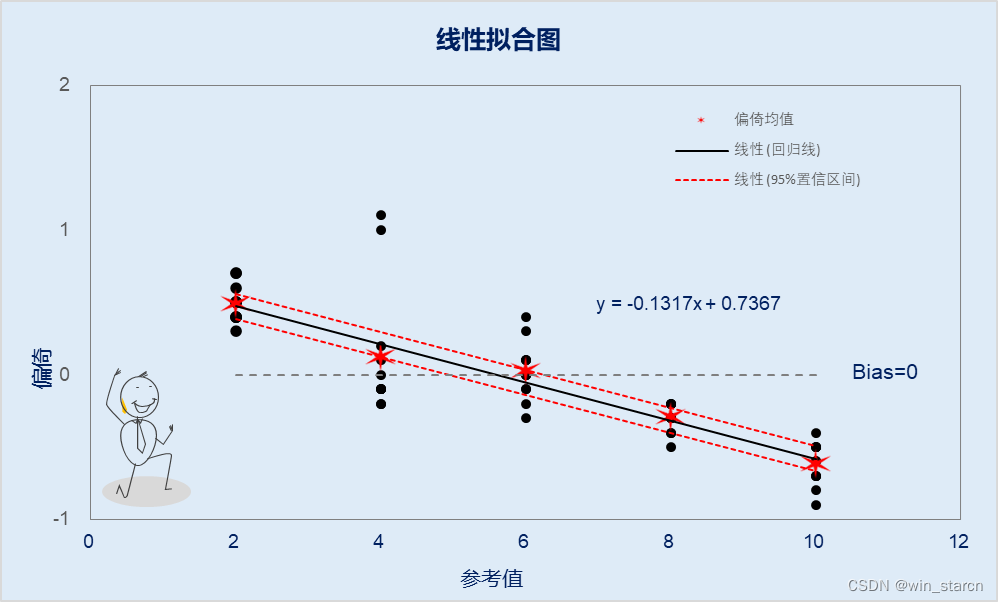
作图的技巧就不再说了

（稍微美化一下，跟手册几乎一模一样）

【步骤7】分析和结论（图示与数值并重的分析结论）

- 线性拟合优度r²=71.4%（开平方后即相关系数，通常0.8~1认为是强相关，基本在边上了），并且对r²还有更多的专业解读，请查阅统计专业书籍进行补充；

​- 根据图形，Bias=0参考线，没有被95%置信区间的两条线包含，认为还是存在线性误差的，特别是基准为4的测量点；

​- 线性误差占比是一个评估指标，Linearity%=100*| a |，通常认为<10%是可接受的（此例中 Linearity% =13.167% 不能接受。

​【步骤8】后续（改进如何做）

​- 后续是否需要对该测量系统进行改进，就要具体问题具体分析了，不再过多解释，可参考手册中的说明（如调整测量系统或r²很优秀的情况下修正）

​- 评价MS的任何特性均要考虑用途是什么

​至此，线性的学习过程基本结束了。容我再啰嗦补充一下：

​- 通常在对计量值的测量系统分析之前，要对采集的数据进行一下“离群值”的检验，因为其对MSA的结果产生重大影响。推荐方法可以是箱线图，以此为例进行说明。

​做个数据辅助区域表：

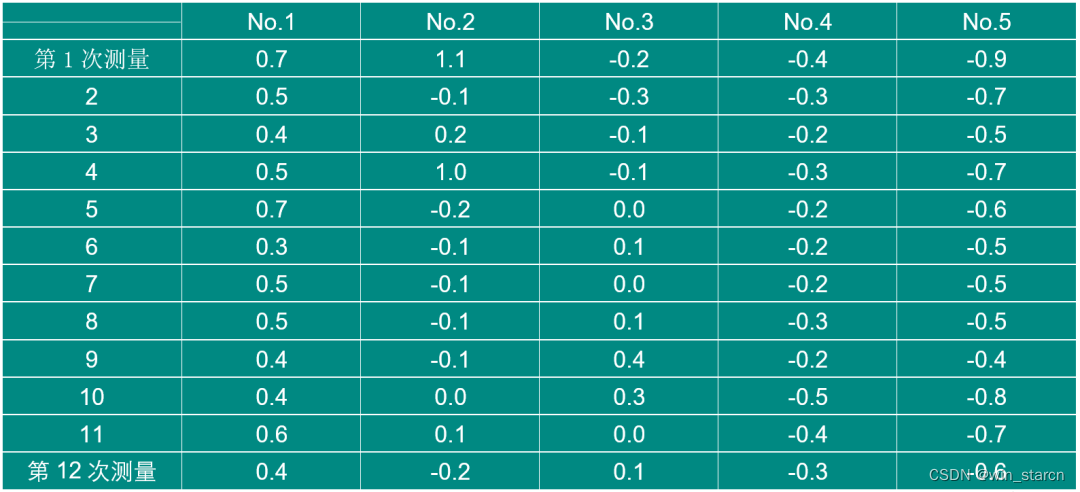
成图（跟手册也基本一模一样，同样需要作图的一些技巧，本文就不做描述了）

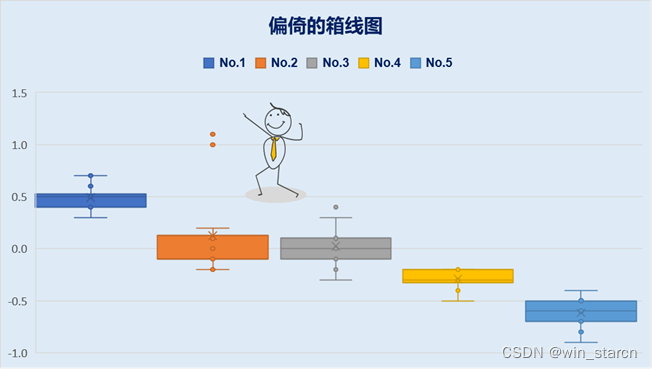
05、结束语

本文仅对“线性”分析的学习过程进行了分享，旨在对手册中指南的一个补充。从工具应用的角度，只要数据丢进Minitab，这些结果瞬间就能得到。以Excel为载体模拟MSA手册中指南的结果，只为在工具应用的角度上更进一步，了解一些背后的知识，如：

- 假设检验

- T检验

- Z检验

- 一元线性回归（相关系数、拟合优度）

​测量系统分析需要具备计量、统计和数学、所在行业的知识，在枯燥的学习中寻找到一种适合的方法是非常不容易的。

​至此，对于位置上的几个评估方法均做了简单的介绍，4篇文章是一个整体，希望能给您学习MSA基础知识带来一些帮助。

感谢阅读，期待与您更多的交流！

文思特（北京）管理咨询有限公司为您整理分享