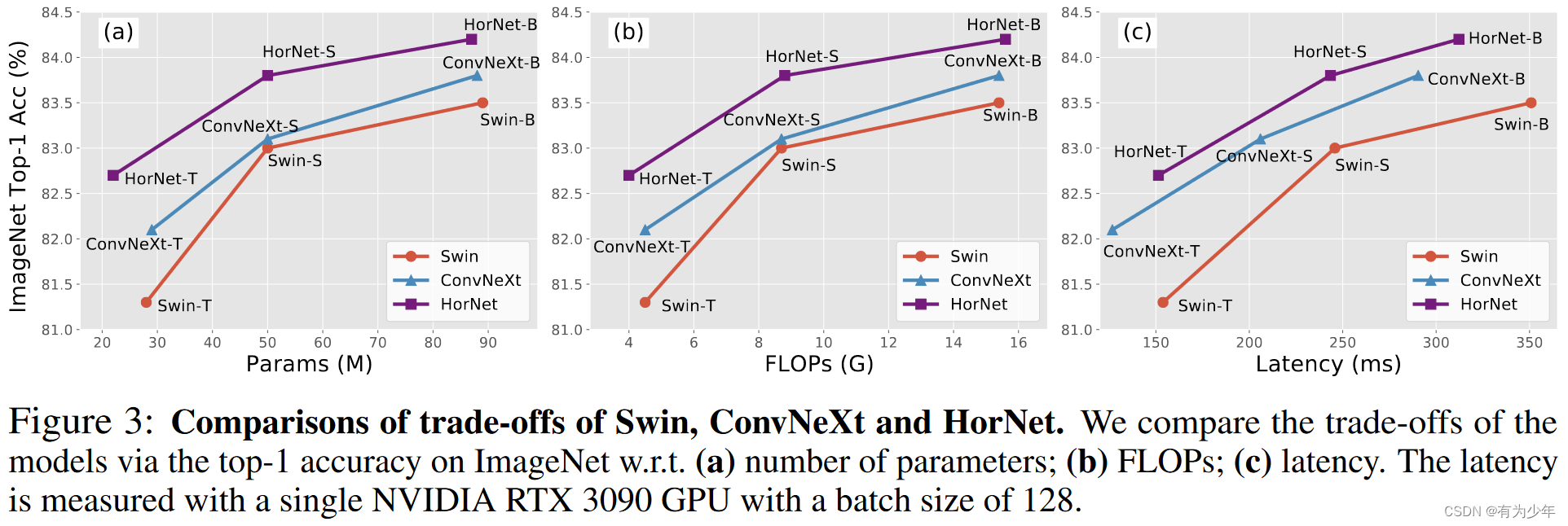
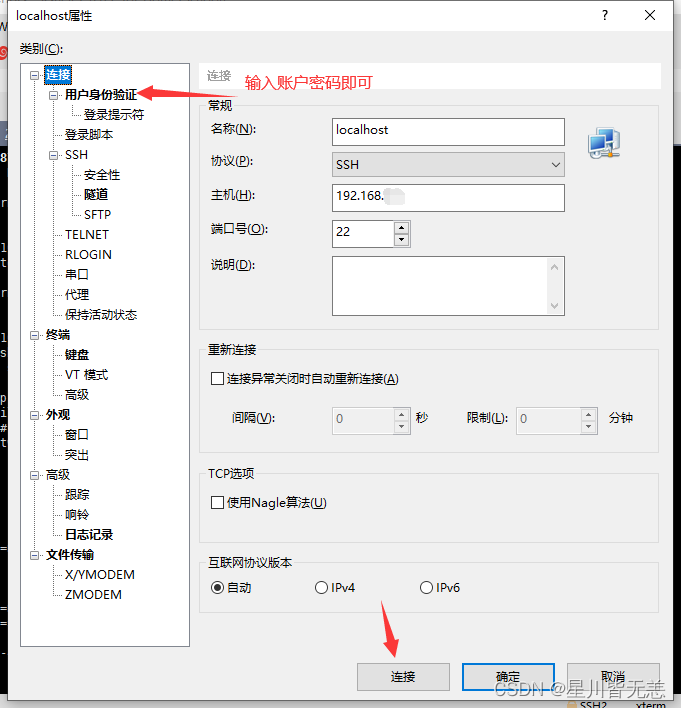
做这道题，走了一个小时的弯路，大冤种是谁我不说🐧 

事情是这样的，大早起八点多钟没啥思路，吃完早饭还困着呢。迷迷糊糊我就想着用C++string的各种函数来解决这道题：

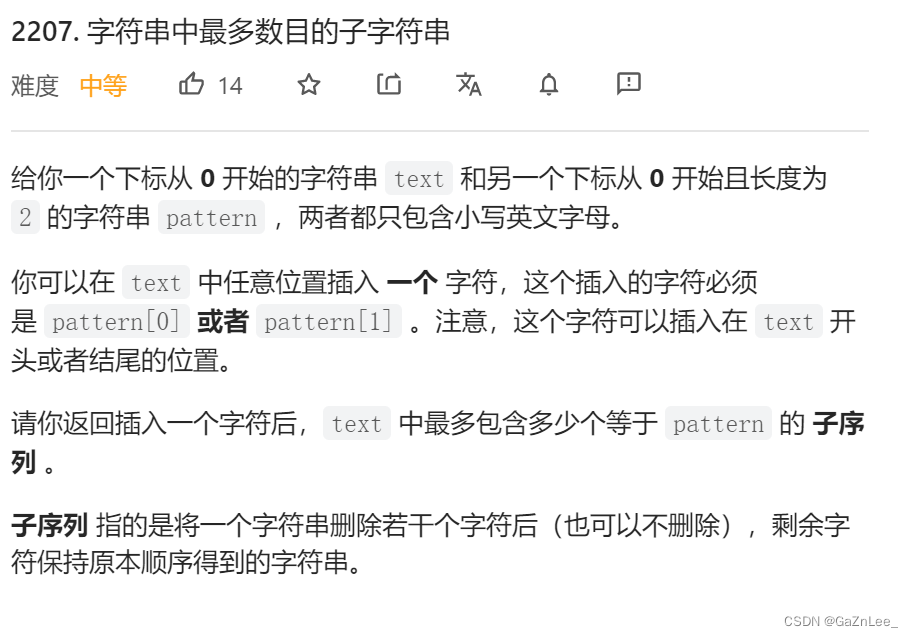
先利用 find 函数确定两字符pattern[0] pattern[1] 在字符串中出现的首位置，之后再利用substr截取字符串，分别统计两字符出现的次数（count函数）。

兜兜转转，又要注意下标又要定义很多子字符串。

代码冗长，本人也很慌张，啊啊啊怎么会如此麻烦且没有技术含量？？？

---

嗯，一定是方法错了。

我开始往算法思想上靠近：由于题目叙述说只能插入一个字符，且要构成数目最多的子字符串，那么无非就两种情况下数目最大：

① pattern[0] 插入，且位于字符串头。

② pattern[1] 插入，且位于字符串尾

终于找到了正确的道路：贪心方法 ＋ 遍历 即可

解题思路：

我们从头到尾开始遍历，设置两变量记录字符串中 pattern[0]  pattern[1]  的数目，遇到 pattern[0] 我们就让 cnt0++ ,遇到 pattern[1]  就让 cnt1++ 。且在遇到 pattern[1] 时，需要更新子字符串的数目，res+=cnt0 ；

上代码：

class Solution {
public:long long maximumSubsequenceCount(string text, string pattern) {int cnt0=0,cnt1=0;long long res=0;int p=0;while(text[p]!='\0'){char c=text[p];if(c==pattern[1]){cnt1++;res+=cnt0;}if(c==pattern[0])cnt0++;p++;}res+=max(cnt1,cnt0);return res;}
};

Notes:

我们新时代的农民工，计数都喜欢从0开始嘛，所以在程序while循环中，我一开始是将 if(c==pattern[0]) 放在前面的，且第二个 if 前面加了 else ，结果是解答错误。原因是：

当 pattern[0]=pattern[1] 时，因为 res 有 +=cnt0 的操作，我们不能把 cnt0++ 放在前面，否则就会多加，例如：

                                                "aabbaca"

                                                "aa"

此时当每遍历到一个 a ，cnt0 都会多加1，不妨拿第一个 a 举例，此时没有满足题意的子字符串，但 res 会在这次遍历之后变成1。并且为了处理两字符相等的情况，第二个 if 不能加 else 。

终于写完啦！ 撒花❀❀