栈和队列OJ题：LeetCode--232.用栈实现队列

news/2024/11/15 21:28:09/

朋友们、伙计们，我们又见面了，今天给大家带来的是LeetCode--232.用栈实现队列

数 据 结 构 专 栏：数据结构

个    人   主    页 ：stackY、

LeetCode 专  栏 ：LeetCode刷题训练营

LeetCode--232.用栈实现队列：https://leetcode.cn/problems/implement-queue-using-stacks/

目录

1.题目介绍

2.实例演示

3.解题思路

3.1创建队列

3.2入列

3.3出列

3.4获取队头元素

3.5优化代码

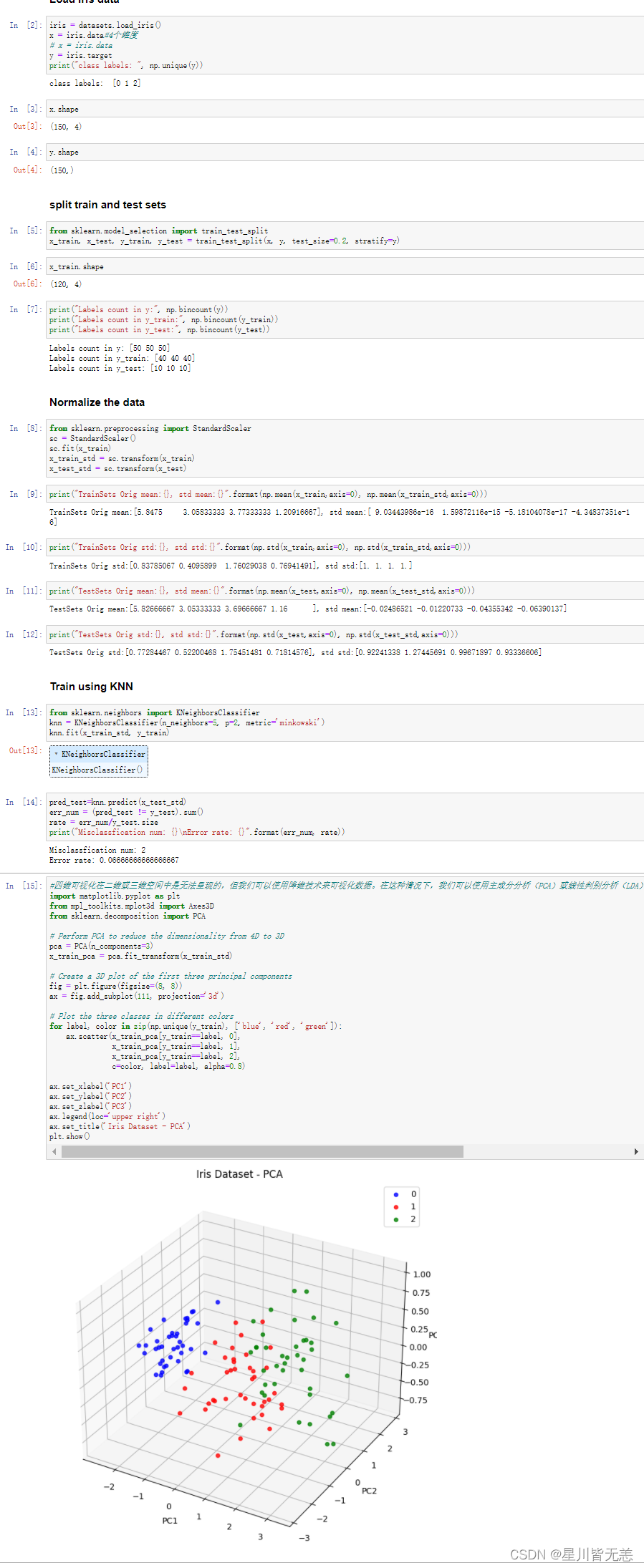
3.6检测队列是否为空

3.7销毁队列 

4.完整代码

1.题目介绍

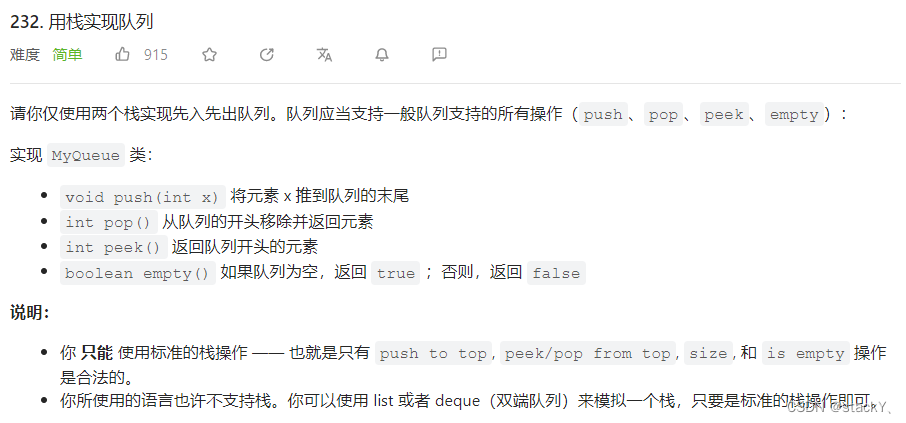
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

        1. void push(int x) 将元素 x 推到队列的末尾
        2. int pop() 从队列的开头移除并返回元素
        3. int peek() 返回队列开头的元素
        4. boolean empty() 如果队列为空，返回 true ；否则，返回 false
说明：

        你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。

你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

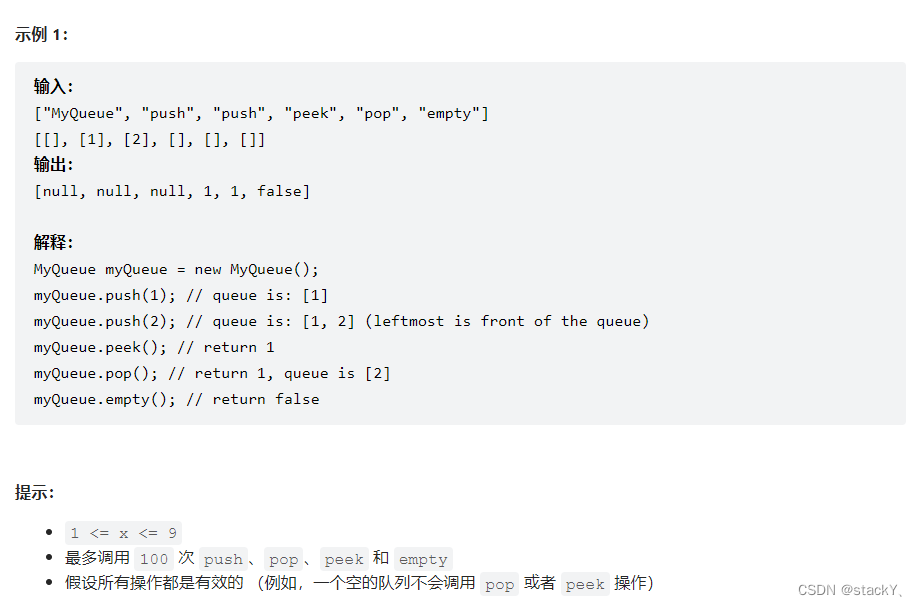
2.实例演示

3.解题思路

在做题之前我们先来进行简单的梳理逻辑，要通过两个栈来实现队列的功能，首先得清楚栈和队列都有什么区别，不熟悉的宝子可以去看看数据结构：栈和队列，队列的功能先进先出，而栈的功能是后进先出，那么有两个栈，要实现队列这种先进先出的功能就比较简单了，可以进行数据的转化，要将数据出队列，那么就需要将这个栈中的数据的前n-1个数据先插入到另外的一个栈，然后再将最后的元素出栈即可，这样就实现了队列的出列操作，那么在入列的时候我们是往哪个栈中入数据呢？所以我们的两个栈分别要有他们的功能，一个用来出数据，另外一个用来入数据，这样子就比较方便了。

3.1创建队列

使用两个栈来实现队列的功能，首先我们得写出一个栈，队列的功能是先进先出，栈的功能是后进先出，在创建队列的时候需要有两个栈，然后为队列创建一块空间，并且将两个栈都进行初始化：

实现栈：

//动态栈
typedef int STDataType;typedef struct Stack
{STDataType* a;int top;        //栈顶int capacity;  //栈的容量
}Stack;//对栈的初始化
void StackInit(Stack* pst);//入栈
void StackPush(Stack* pst, STDataType x);//出栈
void StackPop(Stack* pst);//获取栈顶元素
STDataType StackTop(Stack* pst);//获取栈中的有效元素的个数
int StackSize(Stack* pst);//检测栈是否为空
bool StackEmpty(Stack* pst);//销毁栈
void StackDestroy(Stack* pst);//对栈的初始化
void StackInit(Stack* pst)
{assert(pst);pst->a = NULL;//top为-1时，插入一个数据之后top指向的是刚刚插入数据的位置//pst->top = -1     //top为0时，插入一个数据之后top指向的是刚刚插入数据后面的位置pst->top = 0;pst->capacity = 0;
}//入栈
void StackPush(Stack* pst, STDataType x)
{assert(pst);//检测容量if (pst->top == pst->capacity){int NewCapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;//当pst->a为NULL时执行的功能是和malloc一样STDataType* tmp = (STDataType*)realloc(pst->a, sizeof(STDataType) * NewCapacity);if (tmp == NULL){perror("realloc fail");return;}pst->a = tmp;pst->capacity = NewCapacity;}//入栈pst->a[pst->top] = x;pst->top++;
}//出栈
void StackPop(Stack* pst)
{assert(pst);//判断栈是否为空assert(!StackEmpty(pst));//出栈pst->top--;
}//获取栈顶元素
STDataType StackTop(Stack* pst)
{assert(pst);assert(!StackEmpty(pst));//top指向的是栈顶的下一个位置的元素return pst->a[pst->top-1];
}//获取栈中的有效元素的个数
int StackSize(Stack* pst)
{assert(pst);return pst->top;
}//检测栈是否为空
bool StackEmpty(Stack* pst)
{assert(pst);/*if (pst->top == 0){return true;}else{return false;}*/return pst->top == 0;
}//销毁栈
void StackDestroy(Stack* pst)
{assert(pst);//释放free(pst->a);pst->a = NULL;//重置为0pst->top = pst->capacity = 0;
}

创建队列：

typedef struct {Stack STPush;  //用来出数据的栈Stack STPop;   //用来入数据的栈
} MyQueue;MyQueue* myQueueCreate() {//先为队列开辟一块空间MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));if(obj == NULL){perror("malloc fail");return NULL;}//再初始化栈StackInit(&obj->STPush);StackInit(&obj->STPop);return obj;
}

3.2入列

插入数据就非常简单了，直接将数据插入到我们指定的STPush这个栈中：
代码演示：

void myQueuePush(MyQueue* obj, int x) {StackPush(&obj->STPush, x);
}

3.3出列

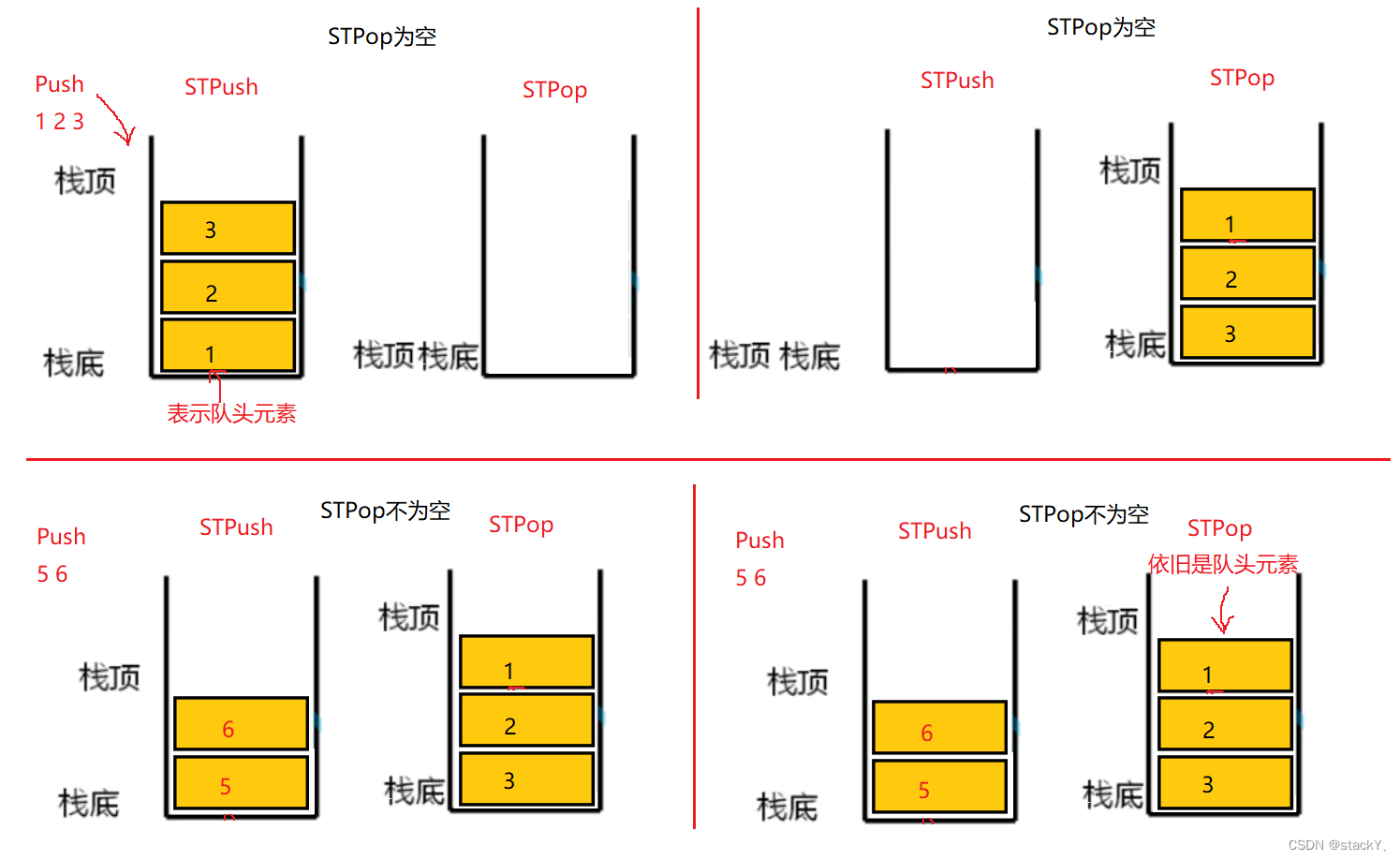
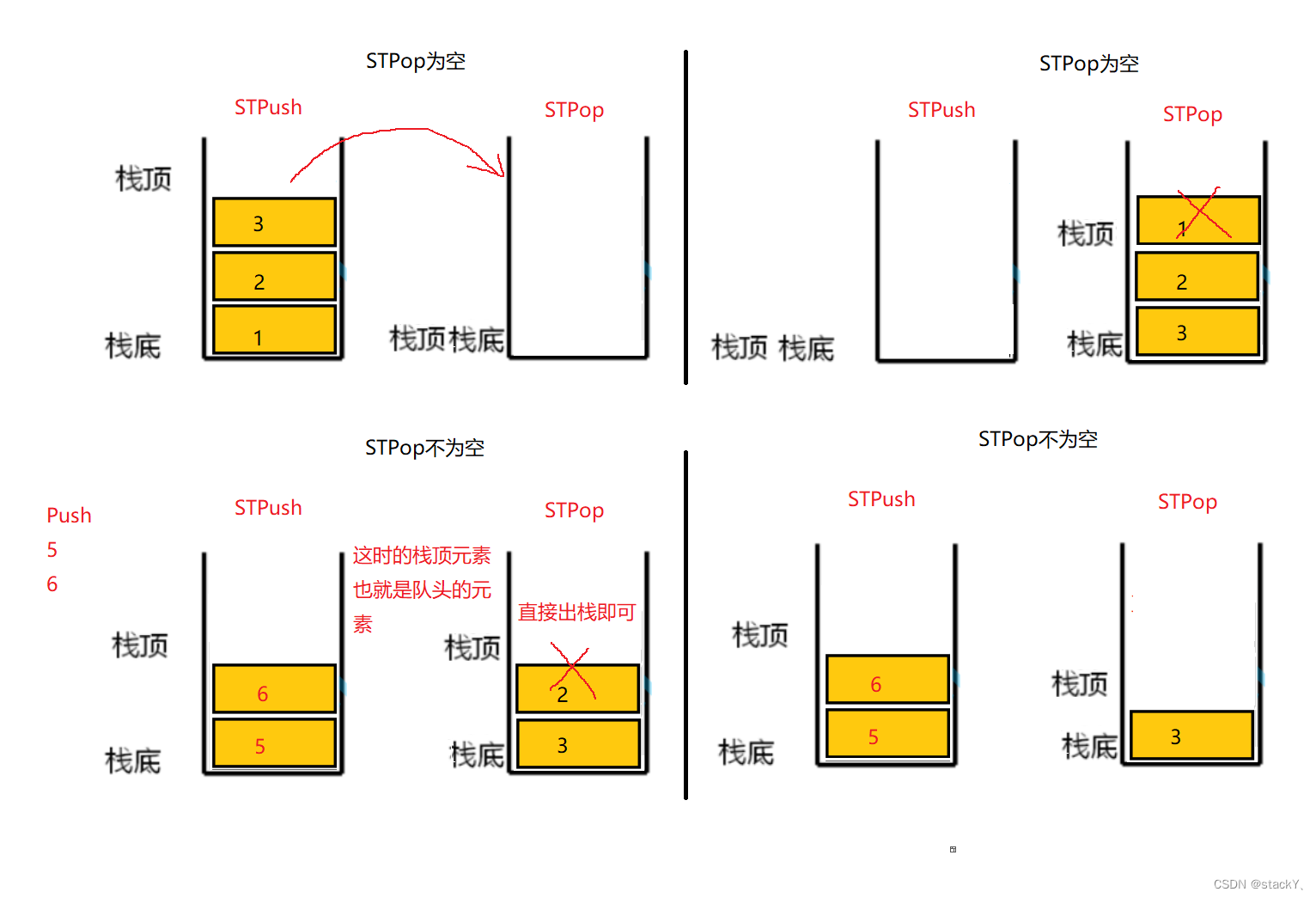
栈的出栈是先进后出，我们有两个栈，因此可以将STPush栈中的前n-1个数据先依次插入到STPop栈中，然后将剩下的最后一个元素，对于队列来说就是队头的数据进行删除即可，但是呢，当第二次删除的时候STPush中没有数据了，这时的STPop中的数据的排列刚好是队列的这种效果，所以可以直接在STPop栈中直接删除即可，所以出列操作需要分两种情况：STPop栈中有无数据

 

代码演示：

 


int myQueuePop(MyQueue* obj) {//判断STPop是否为空if(StackEmpty(&obj->STPop)){//导数据while (StackSize(&obj->STPush) > 1){StackPush(&obj->STPop, StackTop(&obj->STPush));StackPop(&obj->STPush);}//保存队头元素int top = StackTop(&obj->STPush);//删除StackPop(&obj->STPush);return top;}else{int top = StackTop(&obj->STPop);StackPop(&obj->STPop);return top;}
}

3.4获取队头元素

 获取队头元素这里就比较有点麻烦了，先要知道队头元素在哪个栈中，由于我们刚开始设定的缘故，队头的数据是在STPop这个栈中的，这时就需要分两种情况，如果STPop为空，这时就要将STPush中的数据全部插入到STPop中，插入过来之后STPop中的栈顶的数据就是对头的数据，如果STPop不为空，就不需要进行导数据，STPop中的栈顶元素也就是对头的数据：

代码演示： 

int myQueuePeek(MyQueue* obj) {//判断STPop是否为空if(StackEmpty(&obj->STPop)){//全部导过去while (!StackEmpty(&obj->STPush)){StackPush(&obj->STPop, StackTop(&obj->STPush));StackPop(&obj->STPush);}}//再取栈顶元素return StackTop(&obj->STPop);
}

3.5优化代码

如果将出列和获取队头元素这两个函数合在一起看的话还是有许多相似之处，因此我们可以进行改造，在出列时可以直接复用获取队头元素这个函数，这时表现出来的结果就是将STPush中的所有元素都挪动到STPop中，然后再进行删除即可：

 

代码演示：

int myQueuePop(MyQueue* obj) {/*//判断STPop是否为空if(StackEmpty(&obj->STPop)){//导数据while (StackSize(&obj->STPush) > 1){StackPush(&obj->STPop, StackTop(&obj->STPush));StackPop(&obj->STPush);}//保存队头元素int top = StackTop(&obj->STPush);//删除StackPop(&obj->STPush);return top;}else{int top = StackTop(&obj->STPop);StackPop(&obj->STPop);return top;}*///复用int front = myQueuePeek(obj);//删除StackPop(&obj->STPop);return front;
}int myQueuePeek(MyQueue* obj) {//判断STPop是否为空if(StackEmpty(&obj->STPop)){//全部导过去while (!StackEmpty(&obj->STPush)){StackPush(&obj->STPop, StackTop(&obj->STPush));StackPop(&obj->STPush);}}//再取栈顶元素return StackTop(&obj->STPop);
}

3.6检测队列是否为空

队列若为空就表示两个栈都为空，若一个栈不为空，则队列就不为空：

代码演示：

bool myQueueEmpty(MyQueue* obj) {return StackEmpty(&obj->STPush)&& StackEmpty(&obj->STPop);
}

3.7销毁队列 

要销毁队列先要销毁两个栈，然后再将队列释放：

代码演示：

void myQueueFree(MyQueue* obj) {//先释放栈StackDestroy(&obj->STPush);StackDestroy(&obj->STPop);//再释放队列free(obj);
}

4.完整代码


//动态栈
typedef int STDataType;typedef struct Stack
{STDataType* a;int top;        //栈顶int capacity;  //栈的容量
}Stack;//对栈的初始化
void StackInit(Stack* pst);//入栈
void StackPush(Stack* pst, STDataType x);//出栈
void StackPop(Stack* pst);//获取栈顶元素
STDataType StackTop(Stack* pst);//获取栈中的有效元素的个数
int StackSize(Stack* pst);//检测栈是否为空
bool StackEmpty(Stack* pst);//销毁栈
void StackDestroy(Stack* pst);//对栈的初始化
void StackInit(Stack* pst)
{assert(pst);pst->a = NULL;//top为-1时，插入一个数据之后top指向的是刚刚插入数据的位置//pst->top = -1     //top为0时，插入一个数据之后top指向的是刚刚插入数据后面的位置pst->top = 0;pst->capacity = 0;
}//入栈
void StackPush(Stack* pst, STDataType x)
{assert(pst);//检测容量if (pst->top == pst->capacity){int NewCapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;//当pst->a为NULL时执行的功能是和malloc一样STDataType* tmp = (STDataType*)realloc(pst->a, sizeof(STDataType) * NewCapacity);if (tmp == NULL){perror("realloc fail");return;}pst->a = tmp;pst->capacity = NewCapacity;}//入栈pst->a[pst->top] = x;pst->top++;
}//出栈
void StackPop(Stack* pst)
{assert(pst);//判断栈是否为空assert(!StackEmpty(pst));//出栈pst->top--;
}//获取栈顶元素
STDataType StackTop(Stack* pst)
{assert(pst);assert(!StackEmpty(pst));//top指向的是栈顶的下一个位置的元素return pst->a[pst->top-1];
}//获取栈中的有效元素的个数
int StackSize(Stack* pst)
{assert(pst);return pst->top;
}//检测栈是否为空
bool StackEmpty(Stack* pst)
{assert(pst);/*if (pst->top == 0){return true;}else{return false;}*/return pst->top == 0;
}//销毁栈
void StackDestroy(Stack* pst)
{assert(pst);//释放free(pst->a);pst->a = NULL;//重置为0pst->top = pst->capacity = 0;
}typedef struct {Stack STPush;  //用来出数据的栈Stack STPop;   //用来入数据的栈
} MyQueue;MyQueue* myQueueCreate() {//先为队列开辟一块空间MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));if(obj == NULL){perror("malloc fail");return NULL;}//再初始化栈StackInit(&obj->STPush);StackInit(&obj->STPop);return obj;
}void myQueuePush(MyQueue* obj, int x) {StackPush(&obj->STPush, x);
}int myQueuePop(MyQueue* obj) {/*//判断STPop是否为空if(StackEmpty(&obj->STPop)){//导数据while (StackSize(&obj->STPush) > 1){StackPush(&obj->STPop, StackTop(&obj->STPush));StackPop(&obj->STPush);}//保存队头元素int top = StackTop(&obj->STPush);//删除StackPop(&obj->STPush);return top;}else{int top = StackTop(&obj->STPop);StackPop(&obj->STPop);return top;}*///复用int front = myQueuePeek(obj);//删除StackPop(&obj->STPop);return front;
}int myQueuePeek(MyQueue* obj) {//判断STPop是否为空if(StackEmpty(&obj->STPop)){//全部导过去while (!StackEmpty(&obj->STPush)){StackPush(&obj->STPop, StackTop(&obj->STPush));StackPop(&obj->STPush);}}//再取栈顶元素return StackTop(&obj->STPop);
}bool myQueueEmpty(MyQueue* obj) {return StackEmpty(&obj->STPush)&& StackEmpty(&obj->STPop);
}void myQueueFree(MyQueue* obj) {//先释放栈StackDestroy(&obj->STPush);StackDestroy(&obj->STPop);//再释放队列free(obj);
}/*** Your MyQueue struct will be instantiated and called as such:* MyQueue* obj = myQueueCreate();* myQueuePush(obj, x);* int param_2 = myQueuePop(obj);* int param_3 = myQueuePeek(obj);* bool param_4 = myQueueEmpty(obj);* myQueueFree(obj);
*/

今天的博客就分享到这里，喜欢的老铁留下你的三连，感谢感谢！我们下期再见！！ 


http://www.ppmy.cn/news/75914.html

相关文章

Allegro优化布线常用技巧

Allegro优化布线常用技巧

delete-cut 在排线布线过程中，有时候需要调整线序， 这时候，可以使用delete-cut，将需要调整的线， 首尾各剪断一小段线， 这样，中间部分，就变成了dummy net，就可以挂靠任意…
阅读更多...
机器学习与深度学习——通过knn算法分类鸢尾花数据集iris求出错误率并进行可视化

机器学习与深度学习——通过knn算法分类鸢尾花数据集iris求出错误率并进行可视化

什么是knn算法？ KNN算法是一种基于实例的机器学习算法，其全称为K-最近邻算法（K-Nearest Neighbors Algorithm）。它是一种简单但非常有效的分类和回归算法。 该算法的基本思想是：对于一个新的输入样本，通过…
阅读更多...
【设计模式】观察者模式与责任链模式异同点

【设计模式】观察者模式与责任链模式异同点

责任链模式和观察者模式都是常见的设计模式，它们都可以用于解耦和增强代码的可维护性。下面是它们的优劣对比： 责任链模式的优点： 可以动态地组合处理者，增加或删除处理者，而不需要修改客户端代码。可以避免请求发送…
阅读更多...
Linux防火墙之iptables（下）

Linux防火墙之iptables（下）

目录 一、通用匹配 1）协议匹配 2）地址匹配 3）接口匹配 二、隐含匹配 1）端口匹配 2）TCP标志位的匹配 3）ICMP的类型匹配 ①请求规则设置 ②回显匹配 ②显示目的不可达匹配 三、显示匹配 1 &…
阅读更多...
3、EasyExcel介绍

3、EasyExcel介绍

文章目录 EasyExcel介绍1、 导出示例2、 导入示例3、EasyExcel集成3.1 添加依赖 EasyExcel介绍 Java解析、生成Excel比较有名的框架有Apache poi、jxl。但他们都存在一个严重的问题就是非常的耗内存，poi有一套SAX模式的API可以一定程度的解决一些内存溢出的问题&am…
阅读更多...
物业管理可视化大屏

物业管理可视化大屏

物业管理可视化大屏是一种可视化的智能物业管理，它可以将物业管理中的各种数据进行可视化展示，帮助物业管理人员更好地管理社区或园区。 什么是物业可视化数据大屏？ 物业可视化数据大屏就是利用大数据技术，将物业管理中的各种信…
阅读更多...
箭头函数的多线程在开发中的常用配置类

箭头函数的多线程在开发中的常用配置类

拿Runable实现多线程举例，需要实体类继承runnable的接口。然后重新run方法。再新建一个Thread类去执行。我们也可以使用内部类及箭头函数去简化。 内部类 Runnable runnable new Runnable() {Overridepublic void run() {//操作体} }; Thread thread new Thread…
阅读更多...
面试：浏览器从输入url到渲染页面，发生了什么

面试：浏览器从输入url到渲染页面，发生了什么

用户输入阶段合成 URL：浏览区会判断用户输入是合法 URL，比如用户输入的是搜索的关键词，默认的搜索引擎会合成新的，如果符合url规则会根据url协议，在这段内容加上协议合成合法的url 查找缓存 网络进程获取到 URL&am…
阅读更多...
最新文章

Copyright @ 2022~2023