💓博主CSDN主页:杭电码农-NEO💓

⏩专栏分类:数据结构学习分享⏪

🚚代码仓库:NEO的学习日记🚚

🌹关注我🫵带你了解更多数据结构的知识
🔝🔝

在这里插入图片描述

数据结构第八课

1. 前言🚩
2. 求二叉树的高度🚩
3. 查找值为X的节点🚩
4. 二叉树的层序遍历🚩
- 4.1 借助队列实现层序遍历🏁
- 4.2 层序遍历的代码实现🏁
5. 判断一个二叉树是不是完全二叉树🚩
- 5.1 代码实现🏁
6. 二叉树的销毁🚩
7. 链式二叉树题目分享🚩
8. 总结🚩

1. 前言🚩

本节是上一节二叉树知识的延申,这一节中会用到队列的相关知识和二叉树的结构配合使用,如果你还没有接触过队列,那么请先跳转栈和队列详解.如果对二叉树结构与一些基础问题感兴趣的可以跳转二叉树(一)

这里我们直接接着上一章往后介绍

2. 求二叉树的高度🚩

我们还是用之前的二叉树结构来分析:

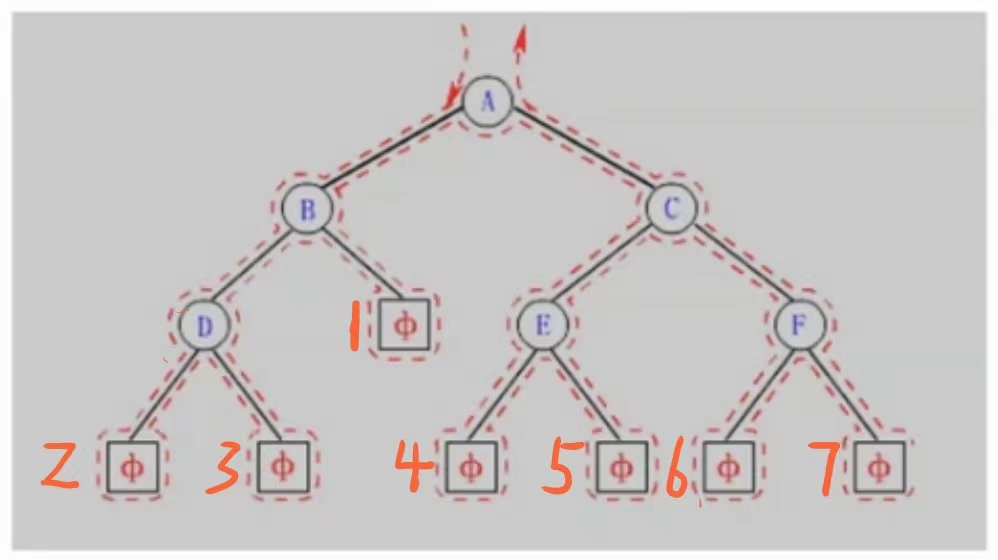在这里插入图片描述这里的空节点我们给赋值成了,1~7.方便我们识别

首先我们要想到的是,当这棵树为空树时,二叉树的高度应该是0,所以当数为空我们返回0,然而当树不等于空时,我们可以以大事化小,小事化了的思想,将当前树的高度转换成左右子树两个中的最大高度再加上一,然后左右子树中最大高度的树的高度又可以转换成我们刚刚的思想,就这样不断递归下去直接我们遇见空节点.

int BinaryTreeDepth(BTNode* root)//求树的高度(按第一层为1的标准)
{if (root == NULL)//树为空或节点为空时返回0{return 0;}//还有一种写法是://return BinaryTreeDepth(root->left) > BinaryTreeDepth(root->right) ?//BinaryTreeDepth(root->left) + 1 : BinaryTreeDepth(root->right) + 1int left = BinaryTreeDepth(root->left);//将值保存起来,否则开辟的栈帧过多int right = BinaryTreeDepth(root->right);return left > right ? left + 1 : right + 1;
}

这里第一步的节点等于空还是有两个涵义,一是我们拿到的树本身就是空树,二是我们递归下去时,遇见了空节点.值得注意的是,这里有两种写法,但是第一种被注释的写法不太好,因为在三目操作符中会不断调用递归函数,这个方法会严重消耗栈帧,所以定义变量将它的值保存起来再比较是优解!

3. 查找值为X的节点🚩

首先我们查找到值后,应该将对应的节点返回到函数外面去,所以这里函数的返回值应该是BTNode*.还是一样的思想

第一步,当树为空树时,里面根本没有节点,所以外面返回空,
第二步,当树或节点不为空时,就应该判断当前节点对应的值是不是与X相同,如果当前节点的值与X相同就应该返回当前节点.
第三步,当我们把一二步都走完后,走到第三步这个位置说明当前节点即不为空节点,并且当前节点对应的值也不为X,那么这时我们就应该去当前节点的左右子树去寻找.

现在来实现代码:

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)//查找值为x的节点,返回节点地址
{if (root == NULL)//空树或空节点就返回空{return NULL;}if (root->data == x)//对应上了就返回节点的地址{return root;}BTNode* left = BinaryTreeFind(root->left, x);if (left != NULL)//left会再次进入到此函数直到遇见NULL或对应值X{return left;//当left不为空时,代表left中一定存储着对应值X的地址}BTNode* right = BinaryTreeFind(root->right, x);if (right != NULL){return right;}return NULL;//当左右子树都为空时,左右子树都不返回,这个节点下面所有的节点都不能与X对应上
}

这里需要解释的是当left不为空指针时,那么left一定是找到了与X值对应上的节点了,因为除了找到对应节点以外,其他情况都是返回空指针,我们就把找到的left返回到上一层函数后,上一层函数发现我们返回的值不为空,又会将这个节点地址返回到上上一层函数,就这样一直返回直到走完所有递归的函数

并且我们这样左子树判断后再定义右子树判断有一个好处,那就是如果左子树找到了,我们就不会走右子树,假如我们像下面这样写的话,不管左子树有没有找到,右子树都会走

    BTNode* left = BinaryTreeFind(root->left, x);BTNode* right = BinaryTreeFind(root->right, x);if (left != NULL)//left会再次进入到此函数直到遇见NULL或对应值X{return left;//当left不为空时,代表left中一定存储着对应值X的地址}if (right != NULL){return right;}return NULL;

这里如果你感到很难理解,应该画一幅递归展开图来分析,假设这里这个图中我需要想找字符’E’.

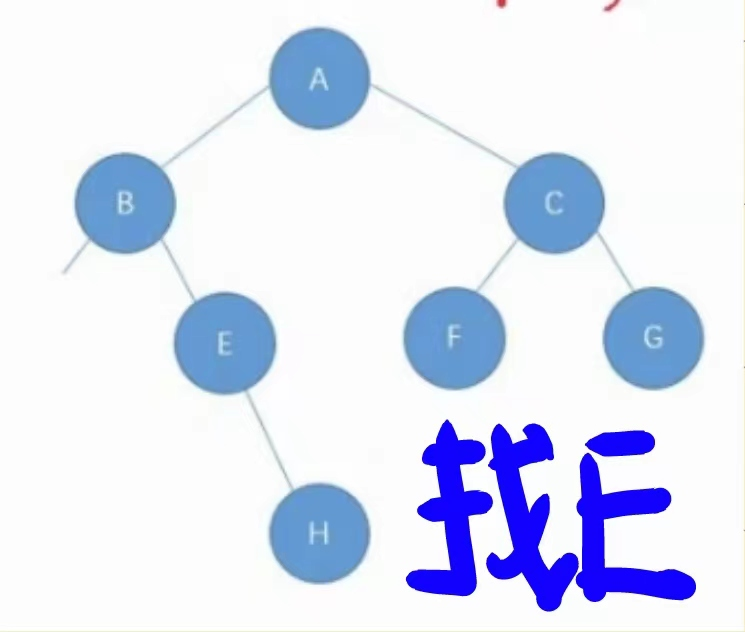
在这里插入图片描述

递归展开图:

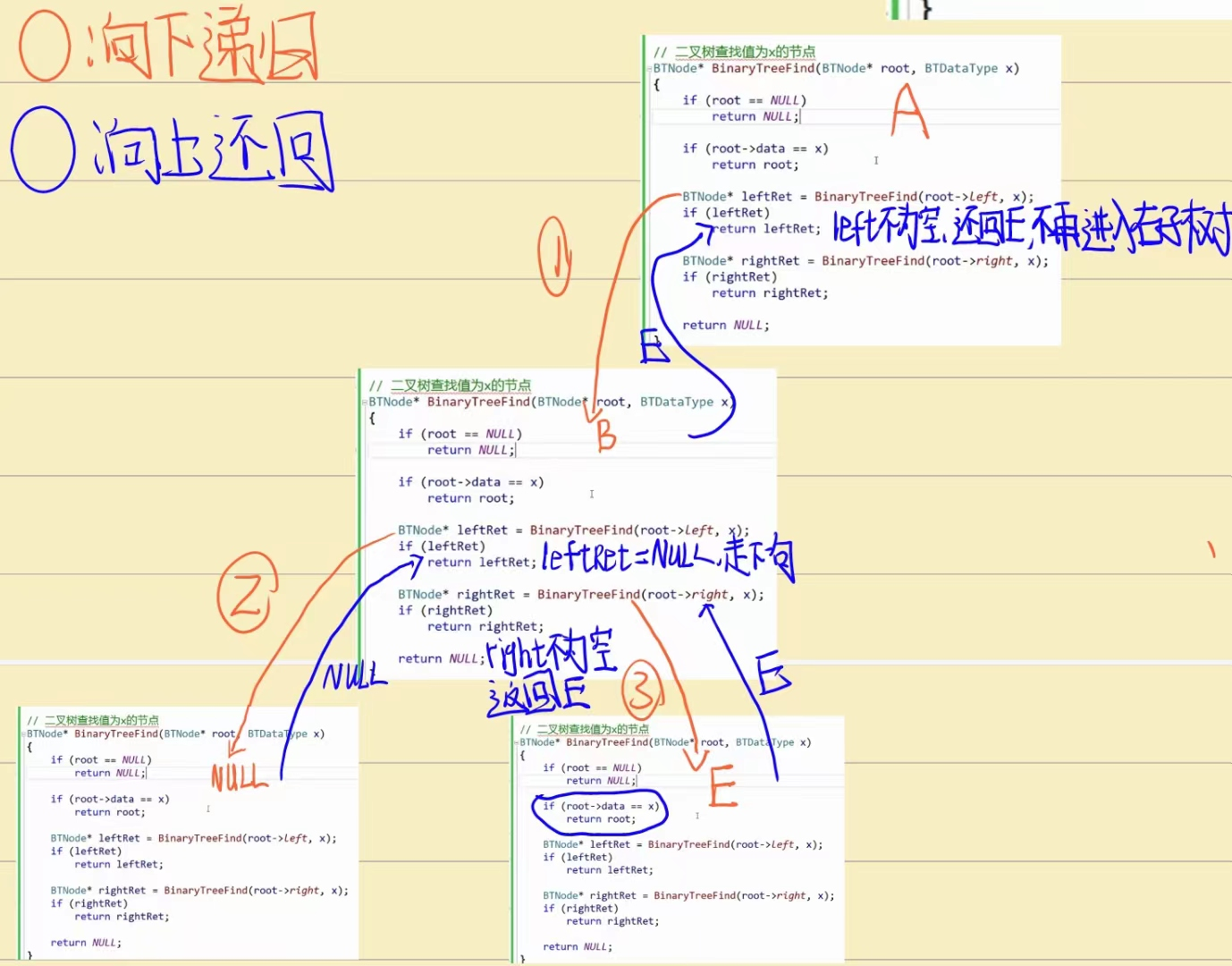
在这里插入图片描述

这里就很好的体现出这样写代码的优势,左子树找到后就直接返回不会进入右子树了

4. 二叉树的层序遍历🚩

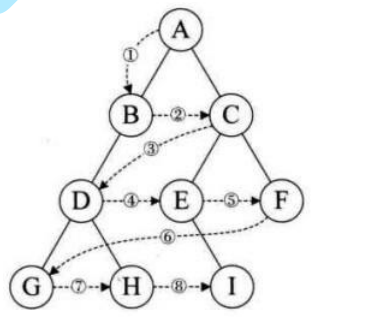
层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

层序遍历的顺序:

在这里插入图片描述

4.1 借助队列实现层序遍历🏁

我们已经了解了层序遍历的顺序,我们自己画一个二叉树的图模拟一下怎样借助队列来实现层序遍历:

在这里插入图片描述
基本步骤是:

先将根入队列
当前节点出队列后,将次此节点的左右孩子入队列
一直这样循环往复直到队列为空,说明最后一层已经没有节点了,遍历结束

我们再来画个图理解一下:

在这里插入图片描述

一直这样循环往复直到队列为空!

4.2 层序遍历的代码实现🏁

void BinaryTreeLevelOrder(BTNode* root)//层序遍历,需要使用队列
{if (root == NULL){return;}Queue q;QueueInit(&q);//先定义一个队列后初始化它,再将根入队QueuePush(&q, root);while (!QueueEmpty(&q))//当队列不为空时就继续{BTNode* front = QueueFront(&q);//将队头出来并打印QueuePop(&q);//取出队头元素并保存在front后将队头删除掉printf("%c ", front->data);if (front->left != NULL)//若孩子不为空就将孩子入队{QueuePush(&q, front->left);}if (front->right != NULL){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);//使用完后销毁队列
}

这样我们就可以将二叉树以层序遍历的方式打印出来:

在这里插入图片描述

5. 判断一个二叉树是不是完全二叉树🚩

判断二叉树是否为完全实际上需要借助我们刚刚介绍的层序遍历的内容,那么怎么判断呢?这里我先不剧透,我们先用一个完全二叉树和一个非完全二叉树来走一走层序遍历看看有没有规律.

1. 完全二叉树的层序遍历

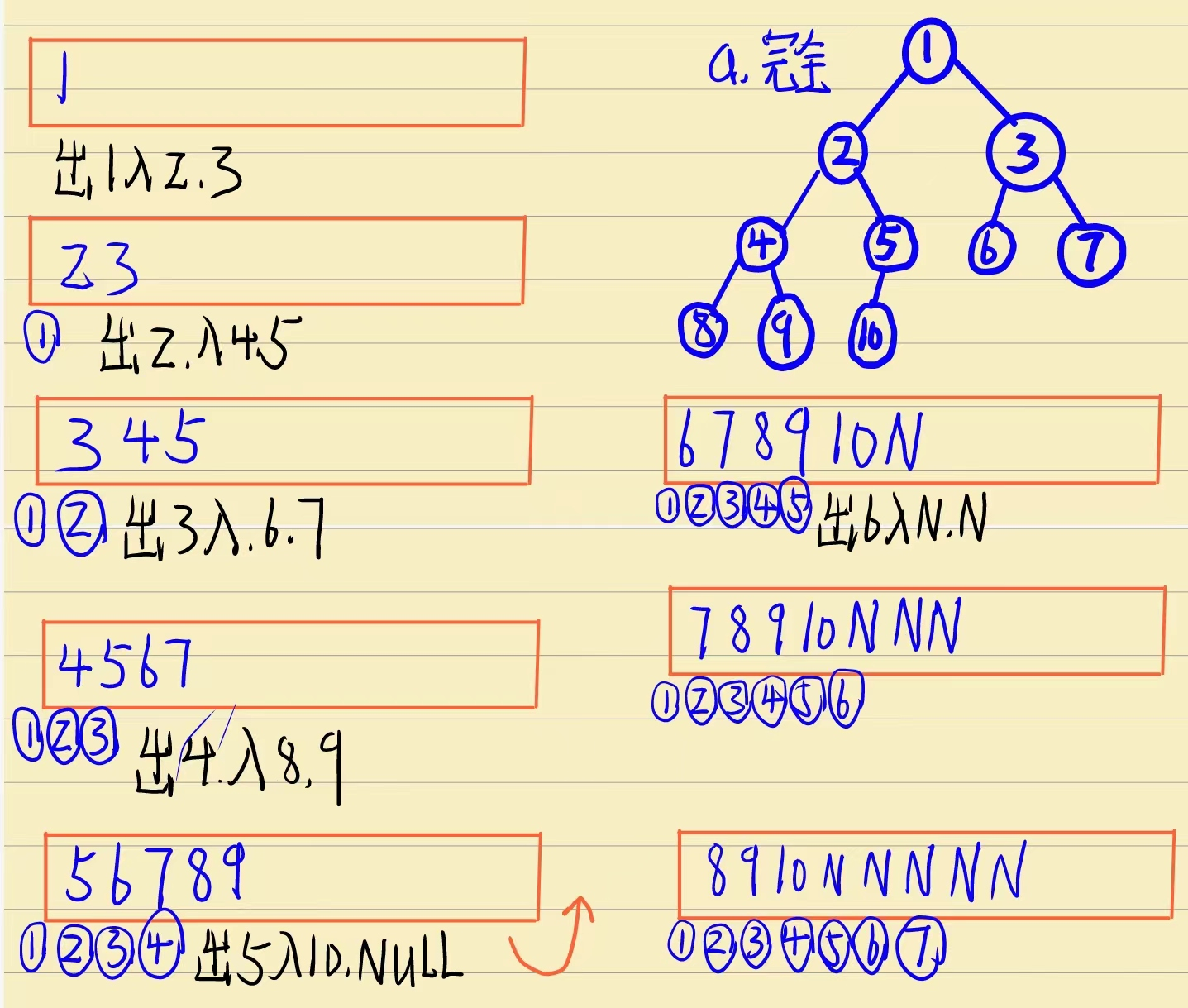
在这里插入图片描述

2. 非完全二叉树的层序遍历:

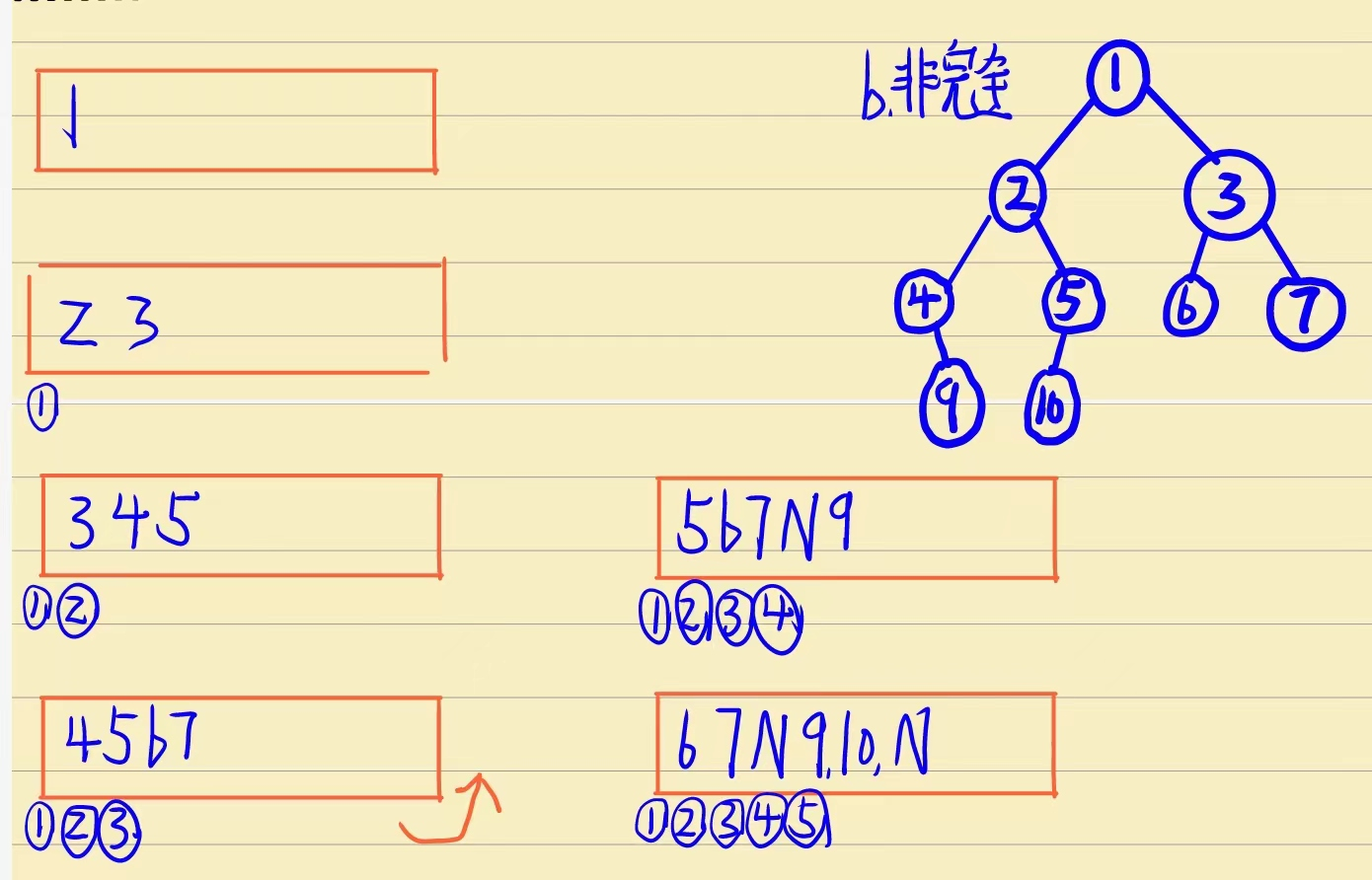
在这里插入图片描述

我们可以发现一个规律,就是完全二叉树在队列中只要遇见了第一个NULL,那么队列后面的内容就全是NULL,而非完全二叉树在队列中遇见了第一个NULL后,后面还会遇见非空元素

5.1 代码实现🏁

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)//当遇见第一个NULL时就直接跳出循环来到下面的语句{break;}else{QueuePush(&q, front->left);QueuePush(&q, front->right);}}// 遇到空了以后，检查队列中剩下的节点// 1、剩下全是空，则是完全二叉树// 2、剩下存在非空，则不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front)//如果不为空就返回false{QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;//全部节点都走完了没有发现非空,说明队列里全是空就返回true.
}

代码的详解已经注释出来了,如果你还不太理解的话,可以直接手动画一个二叉树再来画图判断

6. 二叉树的销毁🚩

这里销毁二叉树右两种写法,一种是传二级指针在函数中将我们事先创建的节点给销毁了,第二种是传一级指针,我们就需要在main函数中将root置空.这里也是用递归的思想.

// 二叉树销毁
//void BinaryTreeDestory(BTNode** root)传二级指针就不用在main函数中将root置空
void BinaryTreeDestory(BTNode* root)//后序遍历释放所有节点(先释放了根会找不到儿子)
{if (root == NULL){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}