F - Max Sum Counting (atcoder.jp)

题意：

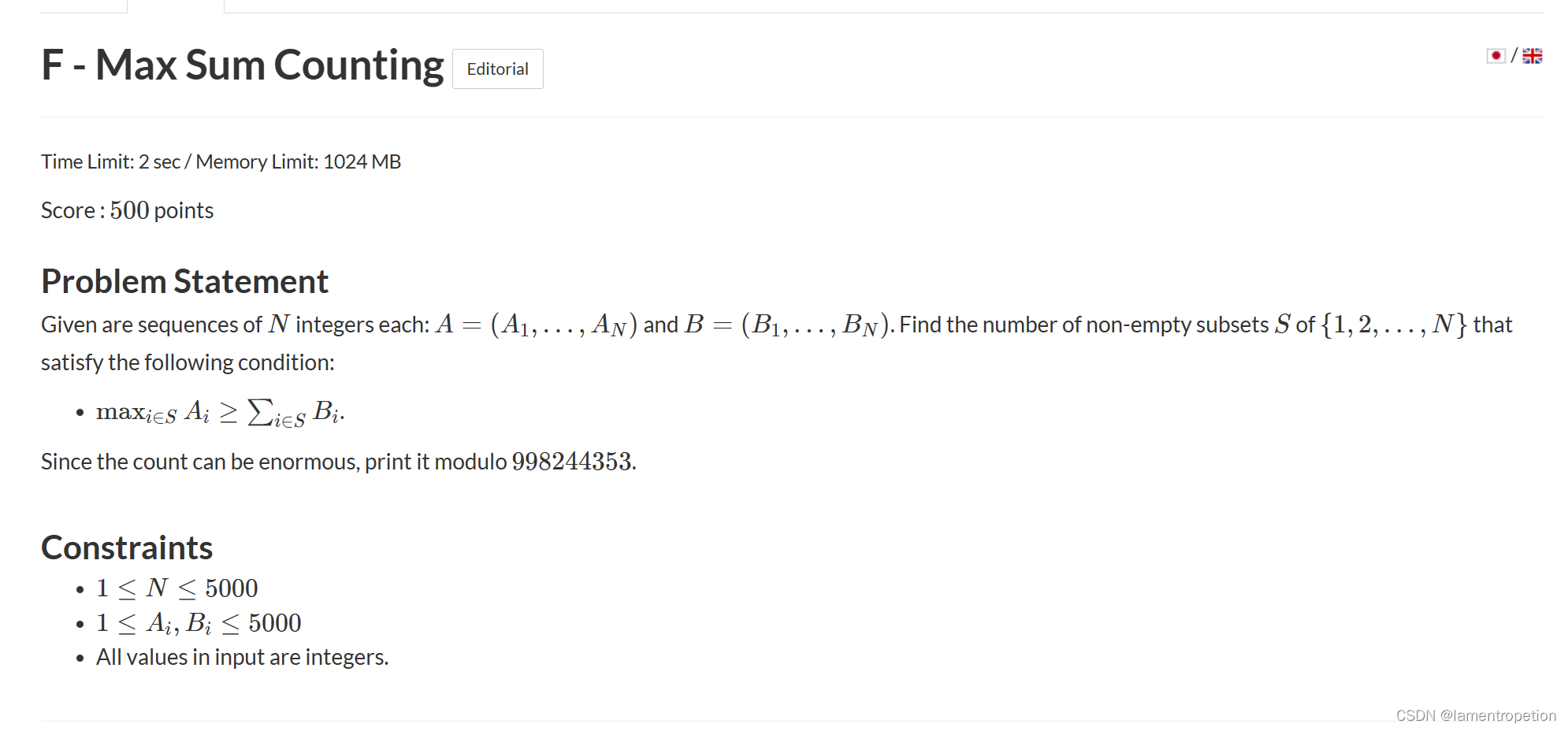
思路：

首先求方案数，除了组合数就是计数DP

但是这道题数据范围是5000，因此考虑DP

因为求的是子集的方案数，因此可以考虑给数组排序

排完序之后做一次背包（子集用背包求）

它的转移条件是A数组中选的最大值>=B数组中选的数的和

这个条件在转移的时候体现

DP中的限制条件除了多一维，也可以在转移的时候加条件

因为已经排好序了，因此选的Ai一定是最大值

那么只需要对B数组做一次01背包即可

Code：

#include <bits/stdc++.h>#define int long longusing namespace std;const int mxn=5e3+10;
const int mxe=1e6+10;
const int mod=998244353;
const int Inf=0x3f3f3f3f;struct ty{int a,b;
}p[mxn];int N;
int dp[mxn];
//选了b数组子集为j的方案数bool cmp(ty x,ty y){return x.a<y.a;
}
void solve(){cin>>N;for(int i=1;i<=N;i++) cin>>p[i].a;for(int i=1;i<=N;i++) cin>>p[i].b;sort(p+1,p+1+N,cmp);dp[0]=1;int ans=0;for(int i=1;i<=N;i++){for(int j=p[i].b;j<=p[i].a;j++){ans+=dp[j-p[i].b];ans%=mod;}for(int j=5000;j>=p[i].b;j--){dp[j]+=dp[j-p[i].b];dp[j]%=mod;}}cout<<ans<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;while(__--)solve();return 0;
}