1. 高斯混合模型概念

        高斯混合模型（Gaussian Mixture Model）是一种聚类算法，它是多个高斯分布函数的线性组合，通常用于解决同一集合下的数据包含多种不同的分布情况。

2.高斯混合模型的一个例子

        在校园里随机抽取2000个学生，其中有男生也有女生，已知男女生的身高都服从高斯分布，这两个高斯分布的均值和方差我们不知道，另外，由于某种原因，我们也不知道这2000个人中有多少个男生有多少个女生，现在我们要求出这两个分布的均值和标准差，还有其权重。

        根据题目的需求，我们需要产生两个高斯分布序列，分别代表男女生的身高。需要注意的是，我们在产生序列的时候必须要在知道男女生各占多少的情况下进行随机生成。但是在求解的过程中，我们必须遵照题意，假设不知道男女生的人数和其各自的均值和方差。然后再对这混合后的2000人序列数据，进行不断地迭代，直到得到的均值和方差趋于平稳。
        

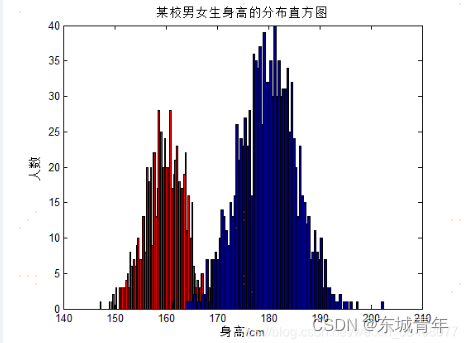
 在图中我们也可以看到，我们生成的女生身高f e m a l e femalefemale服从于N ( 160 ， 16 ) N(160，16)N(160，16),男生身高m a l e malemale服从于N ( 180 , 30 ) N(180,30)N(180,30)。并且其matlab生成该随机序列的代码如下：
 

%绘制男女生身高的例子
clc
clear all
%男女生共取2000人，女生平均身高160，男生平均身高180
female=160+randn(1,821)*sqrt(16);
male=180+randn(1,1179)*sqrt(30);
people=[female male];
figure(1)
hist(people,150);%画出混合后的频率分布直方图
N=100;
figure(2)
hist(female,N);%画出生成的女性的频率分布直方图
h=findobj(gca,'Type','patch');
set(h,'facecolor','r');hold on;%设置柱形图颜色
hist(male,N);%画出生成的男性的频率分布直方图
title('某校男女生身高的分布直方图');
xlabel('身高/cm');ylabel('人数');hold off ;%坐标轴设置

接下来我们就需要对数据进行不断地迭代，从而使其得到两类分布的最优解。

2.1 初始化参数

对于首次迭代，我们需要提供一下，对于男女的均值方差以及权值之间的初始值设定，否则无法启动迭代。这里我们的初始值的设定，我们只需要我们生活中的常识对其进行一下赋初值即可。无需考虑太多。

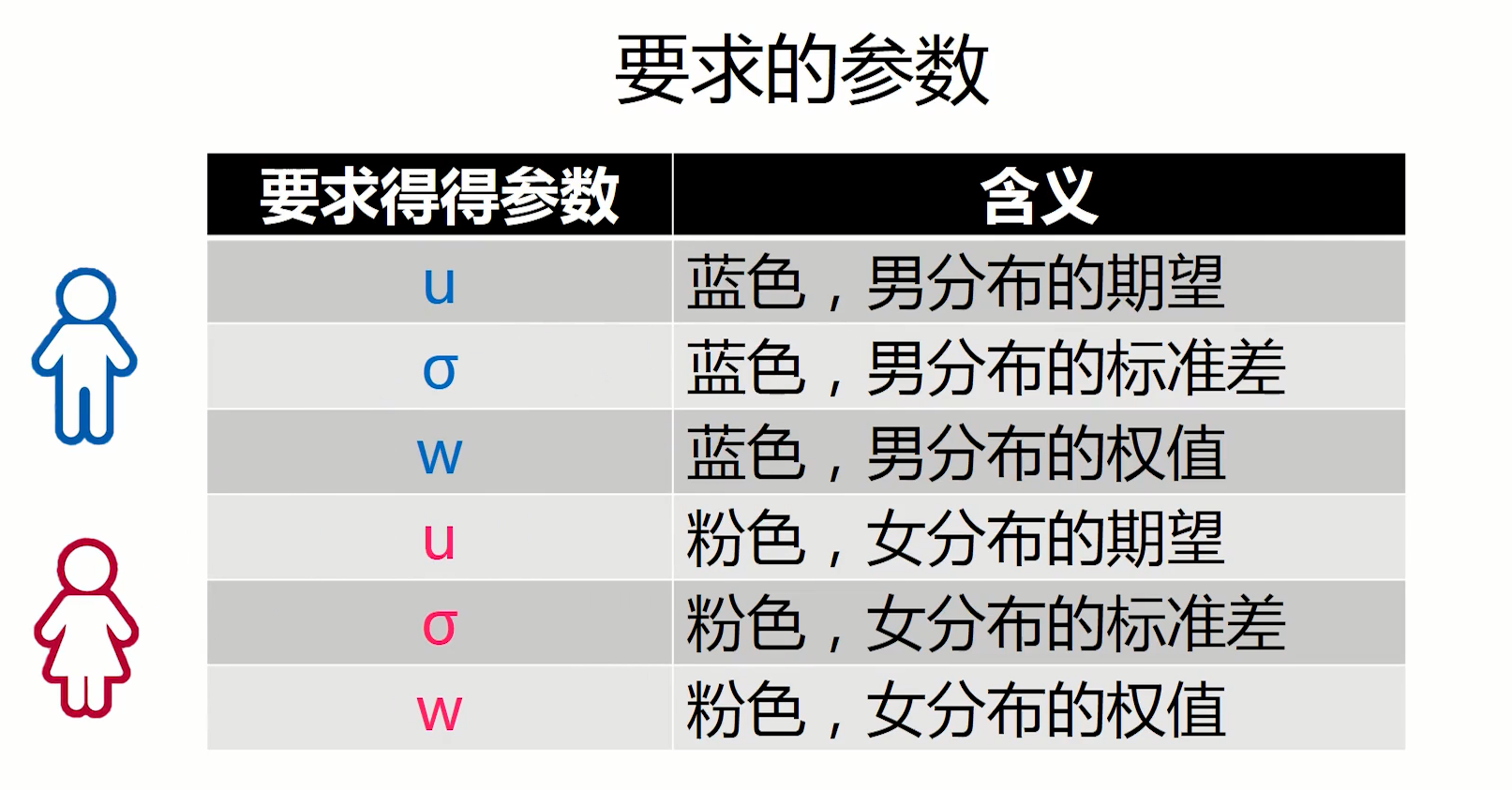
        正如图上所画的，在以后的介绍中，μ ，sigma的颜色不同，代表了性别不同，此处我们以蓝色代表男生的，粉色代表女生的。例如我们在这里的，我假设男女生人数一样多，于是我就对初值进行了如下赋值:

%前提是不知道男女生分布的均值和方差的。
g_mu1=170;g_sigma1=10;g_w1=0.5;%男生的
g_mu2=160;g_sigma2=5;g_w2=0.5;%女生的

2.2 计算每个身高在男分布中的响应R 
 

 通过下面的公式，我们要对我们的2000个混合后的身高数据，利用我们刚刚赋的初值来计算一下每身高hi在男分布中的响应R。所以此处也就一共有2000个响应值。

        在这里或许大家会疑惑，公式中的g (hi∣μ , σ ) 代表的是啥，其实这是一维高斯函数的密度函数，对于我们的这个例子而言，其详细的表达式如下：

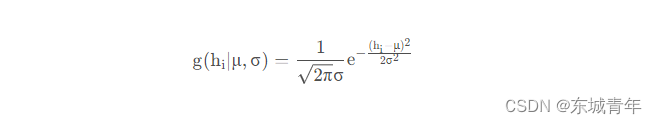
 好了计算完身高在男分布中的响应R ，我们再来计算一下在女分布中的响应R，其求解公式同理。

2.3 更新男女生分布的期望值μ

        由于之前的男女生的期望值μ都是我们凭着主观经验猜测的，所以我们需要对该值进行迭代更新，下面我先介绍男生身高期望值的更新公式。

 

 
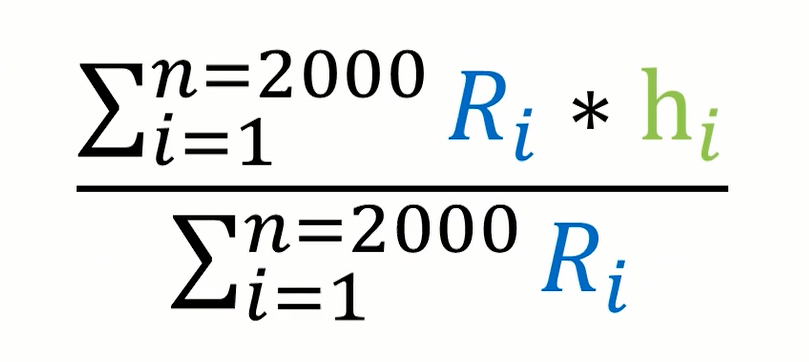
2.4 更新男女生分布的方差σ 2 

        原因同上边一样，我们要通过如下公式更新一下男生分布的方差，其求解公式如下所示：

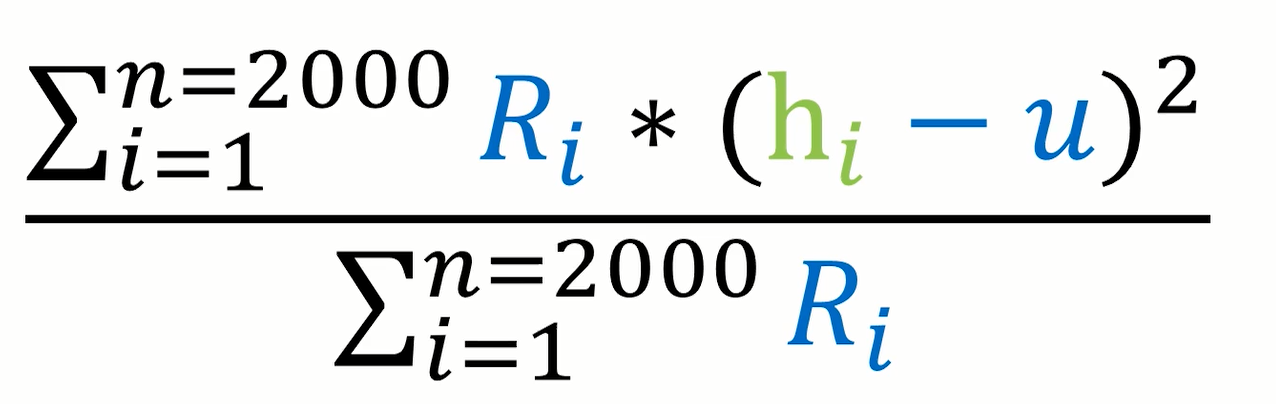
2.5 更新权值ω 1 , ω 2 

男生分布的权值的更新如下：

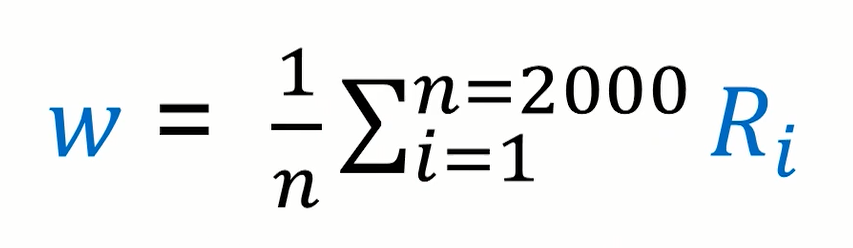
 类似的，女生分布的权值的更新如下：

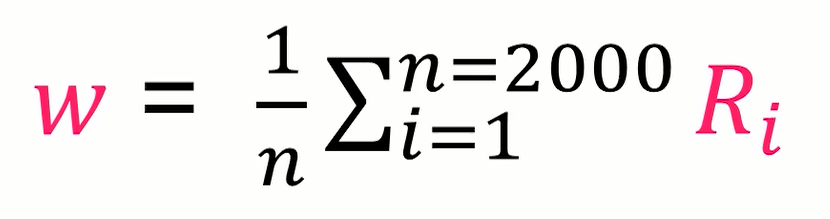
3. matlab源码

3.1 迭代更新的函数封装（matlab）

        由于要使用不断迭代的方式来不断求取新的均值方差权值，以期使得迭代的结果更加接近真实值，于是我对于这部分的代码进行了一下封装，将其封装为一个loop.m文件。其内容具体如下：

文件名称：loop.m
function [ mu1_new,sigma1_new,w1_new,mu2_new,sigma2_new,w2_new ] = loop(male,female,g_mu1,g_sigma1,g_w1,g_mu2,g_sigma2,g_w2 )
%UNTITLED 此处显示有关此函数的摘要
%   此处显示详细说明
%Step 1.首先根据经验来分别设置男女生的均值、方差和权值
% g_mu1=175;g_sigma1=10;g_w1=0.5;%男生的
% g_mu2=158;g_sigma2=10;g_w2=0.5;%女生的%Step 2. 
%计算男的身高在男分布中的响应R1i
%计算女的身高在男分布中的响应R2i
people=[female male];
R1=zeros(1,2000);
R2=zeros(1,2000);
for i=1:2000px1=g_w1*pdf('norm',people(i),g_mu1,g_sigma1);px2=g_w2*pdf('norm',people(i),g_mu2,g_sigma2);R1(i)=px1/(px1+px2);R2(i)=px2/(px1+px2);
end%Step 3.
%更新男、女生身高分布的期望musum1=0;
sum2=0;
for i=1:2000sum1=sum1+R1(i)*people(i);sum2=sum2+R2(i)*people(i);
end
sum11=sum(R1);
sum22=sum(R2);
mu1_new=sum1/sum11;%得出男生的新均值
mu2_new=sum2/sum22;%得出女生的新均值%Step 4.
%更新男、女生身高分布的标准差sigma
sum1=0;
sum2=0;
for i=1:2000sum1=sum1+R1(i)*(people(i)-mu1_new)^2;sum2=sum2+R2(i)*(people(i)-mu2_new)^2;
end
sigma1_new=(sum1/sum11)^0.5;%得出男生的新标准差
sigma2_new=(sum2/sum22)^0.5;%得出女生的新标准差%Step 5.
%更新权值
w1_new=sum11/2000;
w2_new=sum22/2000;end

3.2 主函数实现高斯混合模型GMM

该函数是实现整个这个实例的matlab代码主函数，其内容如下：

文件名称：GMM.m
%绘制男女生身高的例子
clc
clear all
%男女生各取2000人，女生平均身高163，男声平均身高180
female=160+randn(1,821)*sqrt(16);
male=180+randn(1,1179)*sqrt(30);
people=[female male];
figure(1)
hist(people,150);%画出混合后的频率分布直方图
N=100;
figure(2)
hist(female,N);%画出生成的女性的频率分布直方图
h=findobj(gca,'Type','patch');
set(h,'facecolor','r');hold on;%设置柱形图颜色
hist(male,N);%画出生成的男性的频率分布直方图
title('某校男女生身高的分布直方图');
xlabel('身高/cm');ylabel('人数');hold off ;%坐标轴设置%以下通过五个步骤开始构建高斯混合模型%Step 1.首先根据经验来分别设置男女生的均值、方差和权值
%前提是不知道男女生分布的均值和方差的。
g_mu1=170;g_sigma1=10;g_w1=0.5;%男生的
g_mu2=160;g_sigma2=5;g_w2=0.5;%女生的times=10;%设置迭代次数
result=zeros(times,6);%定义一个数组来存储每次的迭代结果
result(1,1)=g_mu1;result(1,2)=g_sigma1;%以下
result(1,3)=g_w1;result(1,4)=g_mu2;
result(1,5)=g_sigma2;result(1,6)=g_w2;%以上将result的第一行设置为初始值for i=1:times-1%调用自己的迭代函数loop来实现迭代计算[ mu11_new,sigma11_new,w11_new,mu22_new,sigma22_new,w22_new ]=loop(male,female,result(i,1),result(i,2),result(i,3),result(i,4),result(i,5),result(i,6));result(i+1,1)=mu11_new;result(i+1,2)=sigma11_new;result(i+1,3)=w11_new;%将每次迭代的结果存入resultresult(i+1,4)=mu22_new;result(i+1,5)=sigma22_new;result(i+1,6)=w22_new ;%当前迭代完成
end
result    % 输出每次迭代结果
figure(3)
%plot(result(:,3),'linewidth',1.5);%画出男生的权重迭代历史
xi=1:0.4:times;
xx=interp1(result(:,3),xi, 'spline');
plot(xx,'linewidth',1.5);%画出男生的权重迭代历史
hold on ;grid on;
yy=interp1(result(:,6),xi, 'spline');
plot(yy,'r','linewidth',1.5);%画出女生权重迭代历史
legend('男生权重变化','女生权重变化','location','northeast');%坐标轴设置
title('男女生权重随迭代次数的变化');
xlabel('迭代次数');ylabel('权重值');axis([1 times 0 1]);%坐标轴设置%开始分别求取出男女生的概率密度函数
%在刚刚的迭代结果中取出男女生的分别的mu和sigma
%男生而言需要求出mu1,sigma1,w1
%女生而言需要求取mu2,sigma2,w2
mu1=result(times,1);
sigma1=result(times,2);
mu2=result(times,4);
sigma2=result(times,5);
figure(4);
%画出男生的概率密度曲线
inter_x=linspace(140,210,500)';
inter_y=normpdf(inter_x,mu1,sigma1);
plot(inter_x,inter_y,'linewidth',1.5);
hold on;
%画出女生的概率密度曲线
inter_yy=normpdf(inter_x,mu2,sigma2);
plot(inter_x,inter_yy,'m','linewidth',1.5)
grid on;
legend('男生','女生');title('男女生身高的概率密度曲线');
xlabel('身高/cm');ylabel('概率');hold off;%坐标轴设置%%此部分开始画高斯混合模型的图像
x =140:0.1:210 ;
y1 = normpdf(x,mu1,sigma1);%定义第1个高斯密度曲线
y2 = normpdf(x,mu2,sigma2);%定义第2个高斯密度曲线
figure(5)
plot(x,y1,'--b','linewidth',1.5);%画出第1个高斯概率密度曲线的图像
hold on;
plot(x,y2,'--g','linewidth',1.5);%画出第2个高斯概率密度曲线的图像
title('两个一维高斯分布HMM模型');xlabel('X');ylabel('概率密度');
% axis([-8 10 0 0.5]);
grid on;%坐标轴设置
tex=text(180,0.1,'当前W1数值为：','FontSize',14,'FontWeight','demi');%图中显示权重
rate=result(:,3)%定义一个权重
c=colormap(lines(times));%定义times条不同颜色的线条
for i=1:timespause(0.1);%延时函数y3=rate(i)*y1+(1-rate(i))*y2%对两个高斯概率密度图像进行加权p2=plot(x,y3,'color',c(i,:),'linewidth',1.5);%绘画加权后的图像num=num2str(rate(i));%将当前第一个高斯概率所用的权重值转为字符串类型tex1=text(203,0.1,num,'FontSize',14,'FontWeight','demi','color','r');%显示当前权重值pause(0.3);%延时函数if(i<times)delete(tex1);%删除当前权重delete(p2);  %删除当前加权后图像end
end
hold off