一、题目描述

给定一个二叉树的根节点 root ，返回它的中序遍历。
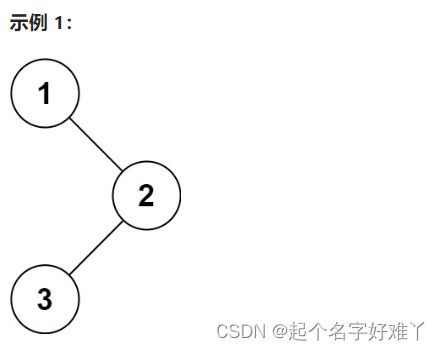
在这里插入图片描述

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

二、解题思路

2.1 递归

先来念一下我们的中序遍历口诀 " 左根右 " “左根右”
对于二叉树的遍历方法基本概念不太了解的可以参考下面的博客：
二叉树的前序/中序/后序遍历新手入门介绍
言归正传：
在这里插入图片描述
递归的代码实现：

class Solution {
public:void LDR(TreeNode* root, vector<int>& vctResult){if(root == nullptr){return;}LDR(root->left, vctResult);vctResult.push_back(root->val);LDR(root->right, vctResult);}vector<int> inorderTraversal(TreeNode* root) {vector<int> vctResult;LDR(root, vctResult);return vctResult;}
};

我们结合代码和图示进行讲解思路：
首先一直往左孩子遍历，直到找到了叶子节点，然后将该节点值保存

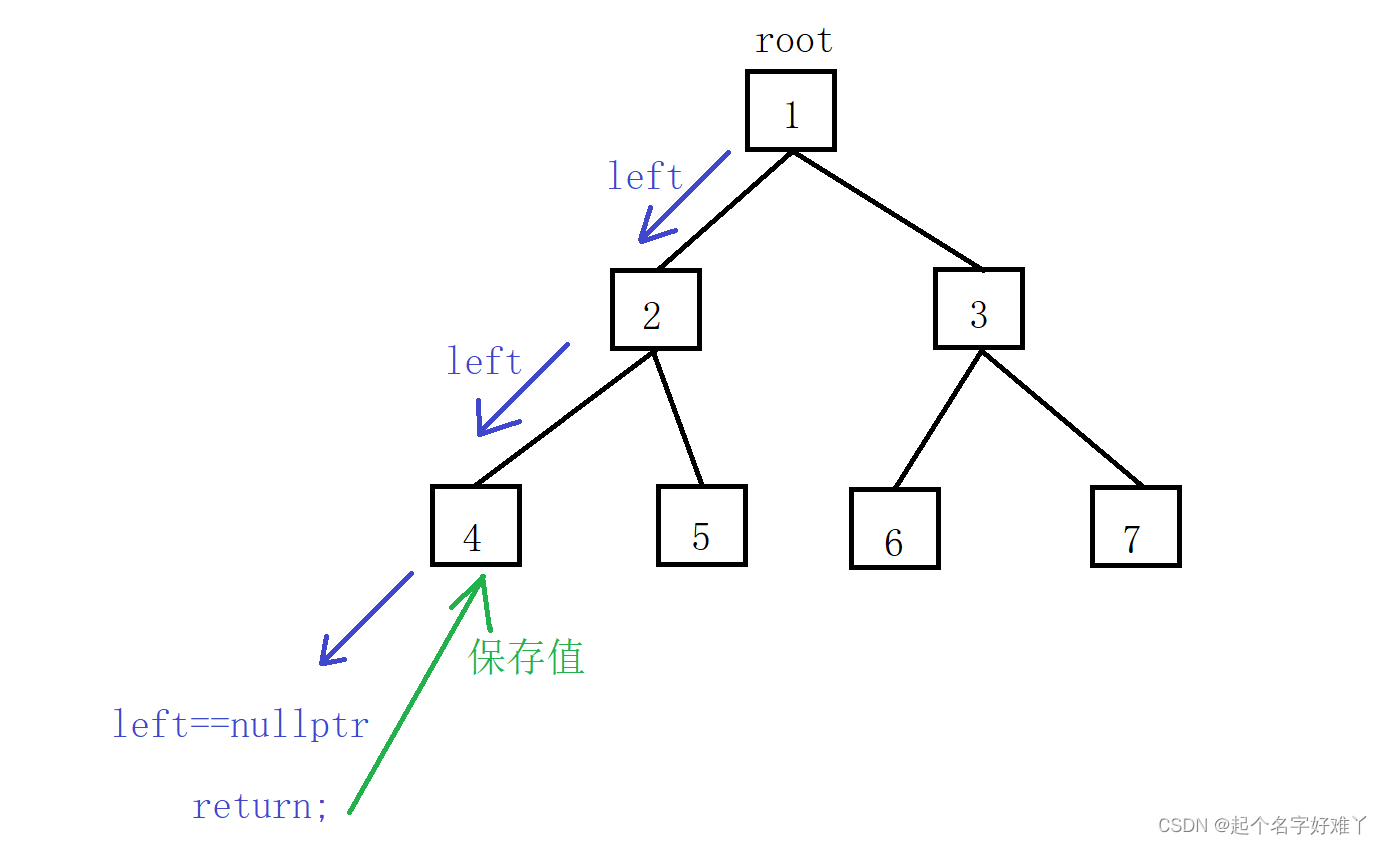
在这里插入图片描述
接下来继续遍历 4 的 right 4 的右孩子也为空，4 的左右子树遍历结束；再次 return 返回上一层即根节点为 2 ，并保存该节点值，节点 2 的左子树已经遍历完毕，接下来遍历 2 的右孩子

结合逻辑，我们再看一下代码的调用关系：
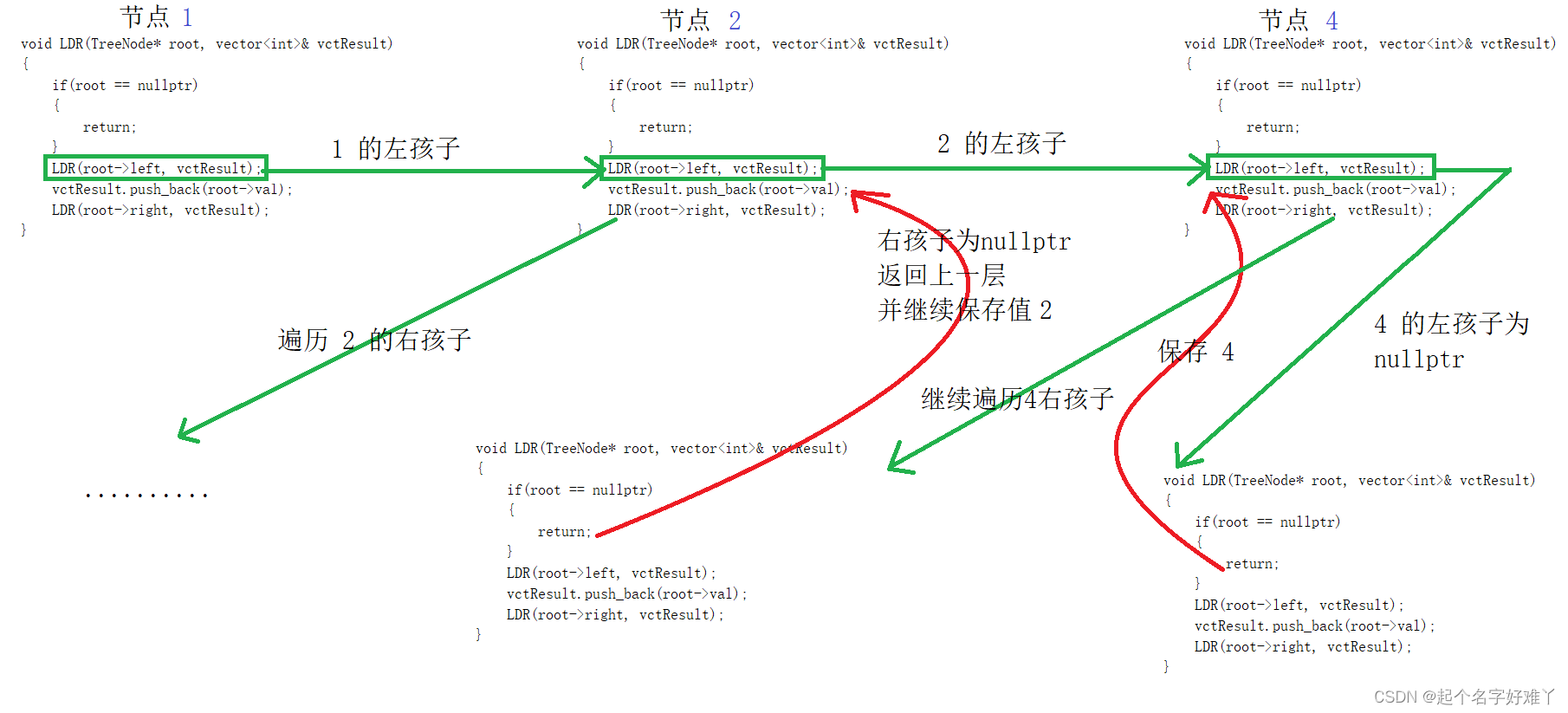
在这里插入图片描述
递归中序遍历运行结果：

2.2 非递归

非递归的中序遍历我们需要借助一个栈来辅助我们遍历
中序遍历，第一个是要找最左的孩子，那么我们就从根开始往左孩子遍历，依次将左孩子入栈，那么，最后一个入栈的，也就是栈顶元素就是最左边的孩子节点
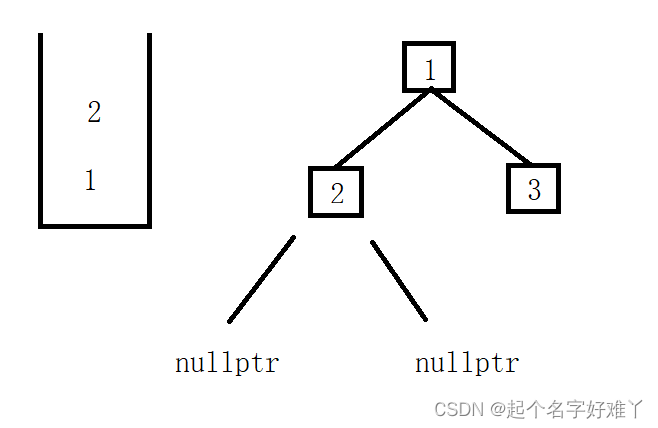
在这里插入图片描述

代码：

            while(root != nullptr){staTemp.push(root);root = root->left;}root = staTemp.top();//取栈顶元素staTemp.pop();vctResult.push_back(root->val);//存值

判断完 2 的左孩子为 nullptr 后，那么意味着 2 没有左，按照左根右的顺序，2 将作为根节点值进行保存，接下俩，按照左根右的顺序，继续遍历 2 的右孩子，若 2 的右孩子不为 nullptr 则继续入栈
即：

root = root->right; //遍历右孩子

2 的右孩子依然为 nullptr，此时栈里还剩元素 1
在这里插入图片描述
代表 1 的左子树已经遍历结束，接下来继续遍历 1 的右孩子，并将 1 pop 出去，保存 1 的值
并继续遍历该节点 1 的右孩子

并继续将 3 入栈，并继续遍历节点 3 的左孩子节点
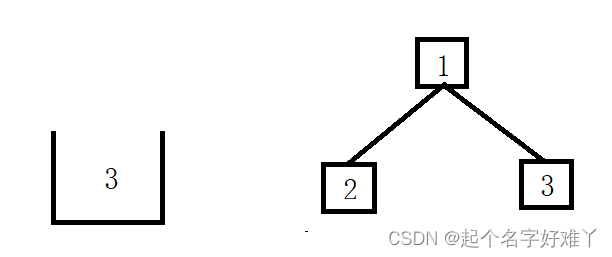
在这里插入图片描述

左孩子为 nullptr 此时栈顶元素为 3 ，将 3 值保存并 pop 出去，并继续遍历 3 的右孩子，3 的右孩子为 nullptr 栈为空且所有节点遍历结束，那么整个中序遍历也已结束。
完整代码示例：

        vector<int> vctResult;  //中序遍历非递归写法stack<TreeNode*> staTemp;while(root != nullptr || !staTemp.empty()) {while(root != nullptr){staTemp.push(root);root = root->left;//遍历左孩子}root = staTemp.top();//取栈顶元素 staTemp.pop();//值取过就 pop出去vctResult.push_back(root->val);root = root->right;//继续遍历右孩子}return vctResult;