目录
- 有序数组
- 哈希表
- 二叉搜索树
- B-Tree
- B+Tree
有序数组
我们指定一个列为索引,然后按照这个列的值排序,以有序数据存放入数据表中,如下所示
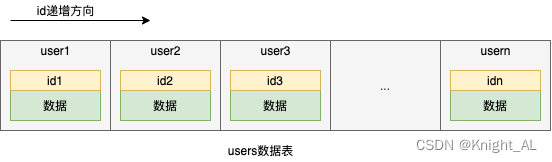
这样,我们在查找数据的时候,就可以通过id这个列,在数据表中进行二分查找,二分查找的时间复杂度为O(logn),这是非常快的
另外由于数据是有序存放的,所以支持范围查找,只要找到起始值然后往后扫描判断,就可以检索出范围内的值
但是使用有序数组的情况,如果是插入或者删除数据,就会非常的麻烦。可以想象,插入数据需要将后半部数据往后挪动一个位置,删除数据需要将后半部数据往前挪动一个位置,这样的代价是非常大的,所以这也是没有使用有序数组来组织索引的原因
哈希表
我们指定一个列为索引,然后将这个列的值作为key,将数据放到哈希表其中的一个bucket中,如下所示
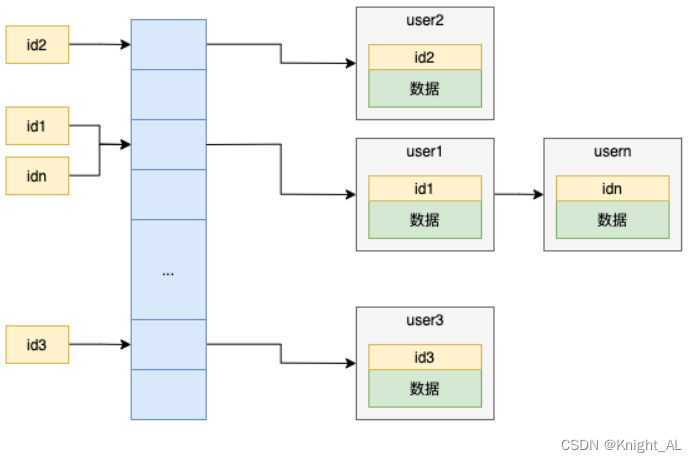
在查找数据的时候,就可以通过id这个列作为key,在哈希表中查找,理论上哈希表的时间复杂度是O(1),所以查找数据会非常快
但是哈希表是无序的,所以我们无法利用索引进行范围查找,只能利用索引来进行等值查询
二叉搜索树
我们指定一个列为索引,然后将这个列的值作为key,来组织一棵二叉搜索树,如下所示
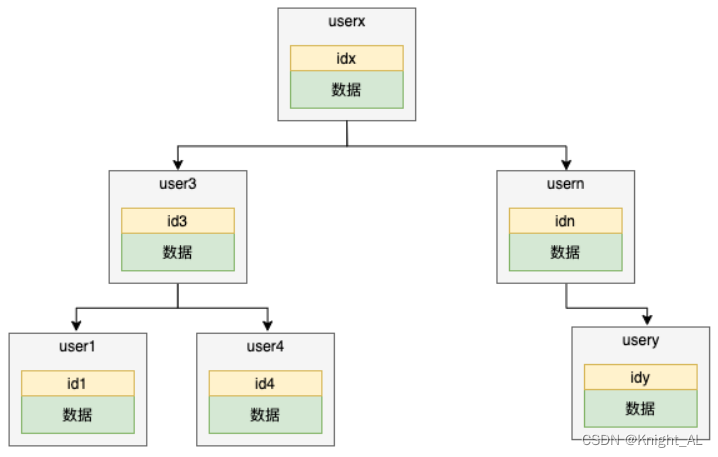
对于平衡二叉树来说,查找的时间复杂度为O(logn),所以查找速度也非常快
二叉搜索树是有序的,所以也支持范围查找
首先我们要明确的一点是,这棵树是存在于磁盘中,每次我们都要从磁盘中读取出相应的节点,然而二叉搜索树的节点在文件中是随机存放的,所以可能读取一个节点就需要一个磁盘IO,恰恰二叉搜索树都会比较高,如一棵一百万个元素的平衡二叉树就有十几层高度了,也就是大部分情况下检索一次数据就需要十几次磁盘IO,这个代价太高了,所以一般二叉搜索树也不会被用来作索引
B-Tree
B-Tree的每个节点都是一个页,可以存放多个数据节点,每页中的节点都是有序的,左子树的节点小于当前节点,右子树节点大于当前节点,InnoDB中规定一个页大小为16K,使用B-Tree作为索引如下所示
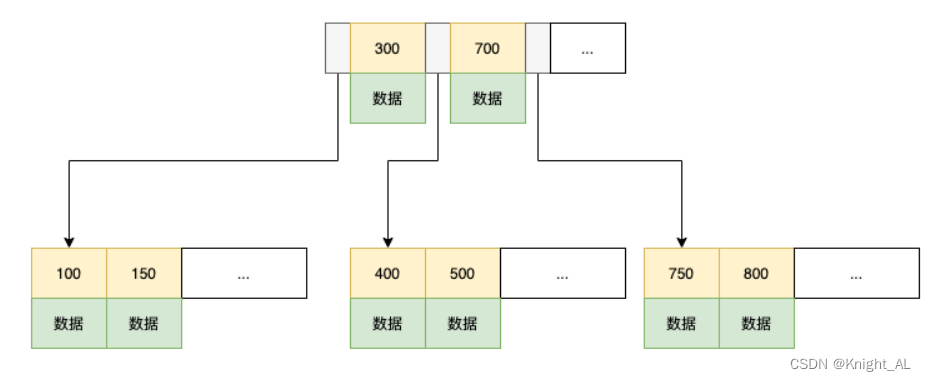
B-Tree的查找过程是,因为每个页中的节点都是有序的,所以在每个页中都可以使用二分查找,而B-Tree的高度又会很低,所以查找效率会很快
一个页有16k,假设平均一条数据大小为100,那么一个页就可以放160条记录,三层高度的B-Tree就可以存放400多万(160160160)条记录,四层高度就可以存放6亿多条记录,B-Tree的高度一般为3-5层。而根节点一般都是缓存在内存中的,所以一般只需要2-4次磁盘IO就可以查询到指定的数据
B+Tree
B+Tree相对于B-Tree,有两个区别
- 非节点只存放索引key,不存放数据,数据只存在于叶子节点
- 叶子节点页之间使用链表连接
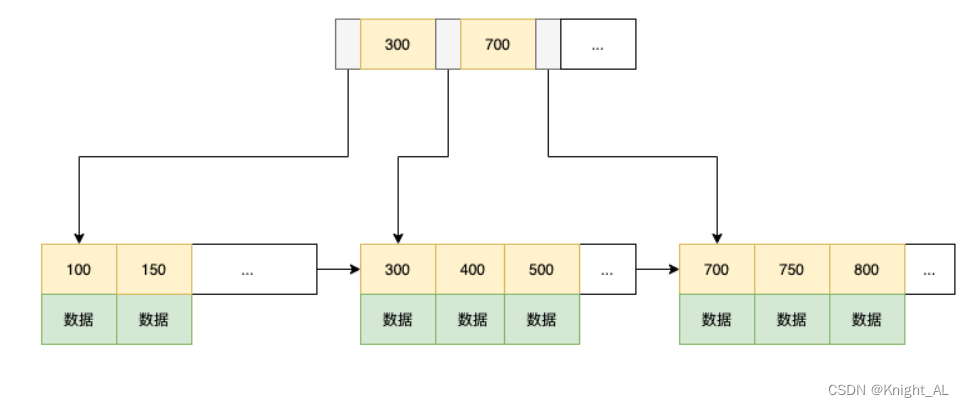
因此带来的几个好处
- B+Tree的磁盘读写代价更低:由于非叶子节点只存放索引不存放数据,所以每个节点可以存放更多的索引,一次读取查找的关键字更多,树的高度更低
- B+Tree的查询效率更加稳定,因为只有叶子节点存在数据,所以每次查询的路径长度都是相同的
- B+Tree更适合范围查询,因为B-Tree的非叶子节点存放数据,所以需要使用中序遍历来查询,- 而B+Tree只有叶子节点有数据,叶子节点之间使用链表连接,所以只要顺序扫描进行,更加方便
基于上述的原因,B+Tree比B-Tree更适合做数据库索引