文章目录
- 【半监督医学图像分割 2023 MICCAI】SCP-Net
- 摘要
- 1. 简介
- 2. 方法
- 2.1 自交原型预测
- 2.2 典型预测不确定性
- 2.3 无监督原型一致性约束
- SPCC
- CPCC
- 3 实验与结果
- 3.1 数据集和评价指标
- 3.2 实施细节
- 3.3 与其他方法的比较
- 3.4 消融研究
- 4. 总结
【半监督医学图像分割 2023 MICCAI】SCP-Net
论文题目:Self-aware and Cross-sample Prototypical Learning for Semi-supervised Medical Image Segmentation
中文题目:自感知交叉样本原型学习用于半监督医学图像分割
论文链接:https://arxiv.org/abs/2305.16214
论文代码:
论文团队:
发表时间:
DOI:
引用:
引用数:
摘要
一致性学习在半监督医学图像分割中起着至关重要的作用,它可以有效地利用有限的标注数据,同时充分利用丰富的未标注数据。
一致性学习的有效性和效率受到预测多样性和训练稳定性的挑战,而这两个问题往往被现有的研究所忽视。 同时,用于训练的标记数据数量有限,往往不足以形成伪标记的内部紧凑性和类间差异。
- 为了解决这些问题,我们提出了一种自感知的跨样本原型学习方法(SCP-NET),通过利用从多个输入中获得的更广泛的语义信息来提高一致性学习中预测的多样性。
- 此外,我们引入了一种
自我感知的一致性学习方法,该方法利用未标记数据来提高每个类中伪标记的紧凑性。 - 此外,在跨样本原型一致性学习方法中引入了双损失重加权方法,以提高模型的可靠性和稳定性。
通过对ACDC数据集和Promise12数据集的大量实验,验证了SCP-NET的性能优于现有的半变量分割方法,并与有限监督训练相比取得了显著的性能提高。 我们的代码很快就会来。
1. 简介
随着人们对准确高效的医学图像分析的需求日益增加,半监督分割方法为解决标记数据稀少和对人工专家标注的依赖提供了一个可行的解决方案。 对数据集中的所有图像进行注释通常是不可行的。 通过探索未标记数据中包含的信息,半监督学习[1,2]可以帮助提高分割性能,而不是只使用少量的注释示例集。
一致性约束是半监督分割中广泛使用的一种解决方案,它通过使预测和/或中间特征在不同的扰动下保持一致来提高分割性能。 然而,在不同的任务中获得普遍和适当的扰动(例如,增强[3]、上下文[4]和解码器[5])是一个挑战。 此外,在半监督分割模型中使用的一致性损失的有效性可能会被对预测结果没有明显影响的微小扰动所削弱。 反之,不适当的扰动或结构间边界不清会引入不准确的监控信号,导致误差积累并导致模型的次优性能。 近年来,一些无监督原型分割方法[6,7,8]将特征匹配操作应用于半监督分割任务中的伪标签生成。 然后,对模型的预测与相应的原型预测进行一致性约束,以提高模型的性能。 例如,许等人。 [6]提出了一个循环原型一致性学习框架,它涉及标记数据和未标记数据之间的双向信息流。 吴等人。 [7]建议通过促进类特性的对齐来促进类特性向相应的高质量原型的汇聚。 张等人。 [8]利用与原型的特征距离来促进训练课程中对伪标签的在线纠正。 文献[6,7,8]中所用的全局范畴原型由于受到原型数量的限制,可能会忽略多样性,损害表示能力。
简单地说,以前的研究忽略了考虑预测结果对扰动响应的鲁棒性和可变性。 为了解决这个问题,与[6,7]中的全局原型不同,我们引入了自感知和跨样本类原型,它们产生两个不同的原型预测,以增强语义信息交互并确保一致性训练中的分歧。 我们还利用自感知原型预测和多个预测之间的预测不确定性来重新加权交叉样本原型的一致性约束损失。 通过这样做,我们可以在低对比度区域或粘合边缘等具有挑战性的区域减少标签噪声的不利影响,从而产生更稳定的一致性约束训练过程。 反过来,这将大大提高模型的性能和精度。 最后,我们提出了一个无参数的半监督分割框架SCP-Net,它结合了这两种原型一致性约束。
本文的主要贡献可以概括如下:
(1)对基于原型的半监督分割方法进行了深入研究,提出了自感知原型预测和跨样本原型预测,以保证一致性学习中适当的预测多样性。
(2)为了提高伪标签的类内紧致性,提出了一种Selfaware原型一致性学习方法。
(3)为了提高跨样本原型一致性学习的稳定性和可靠性,我们设计了一种双损失重加权方法,减少了噪声伪标签的负面影响。
(4)在ACDC和Promise12数据集上的大量实验表明,SCP-net有效地利用了未标记数据,提高了半监督分割性能,标注率低至10%。
2. 方法
在半监督分割任务中,训练集被划分为标记集 D l = { ( x k , y k ) } k = 1 N l \mathcal{D}_{l}=\{(x_{k},y_{k})\}_{k=1}^{N_{l}} Dl={(xk,yk)}k=1Nl和未标记集 D u = { x k } k = N l + 1 N l + N u \mathcal{D}_{u}=\{x_{k}\}_{k=N_{l}+1}^{N_{l}+N_{u}} Du={xk}k=Nl+1Nl+Nu,其中 N u ≫ N l N_{u}\gg N_{l} Nu≫Nl。 每个标记图像 x k ∈ R H × W x_{k}\in\mathbb{R}^{H\times W} xk∈RH×W都有其地真值掩码 y k ∈ { 0 , 1 } C × H ^ × W y_{k}\in \{0,1\}^{C\times\hat{H}\times W} yk∈{0,1}C×H^×W,其中h、w和c分别是高度、宽度和类数。 我们的目标是通过从未标记的数据集中提取额外的知识来提高模型的分割性能。
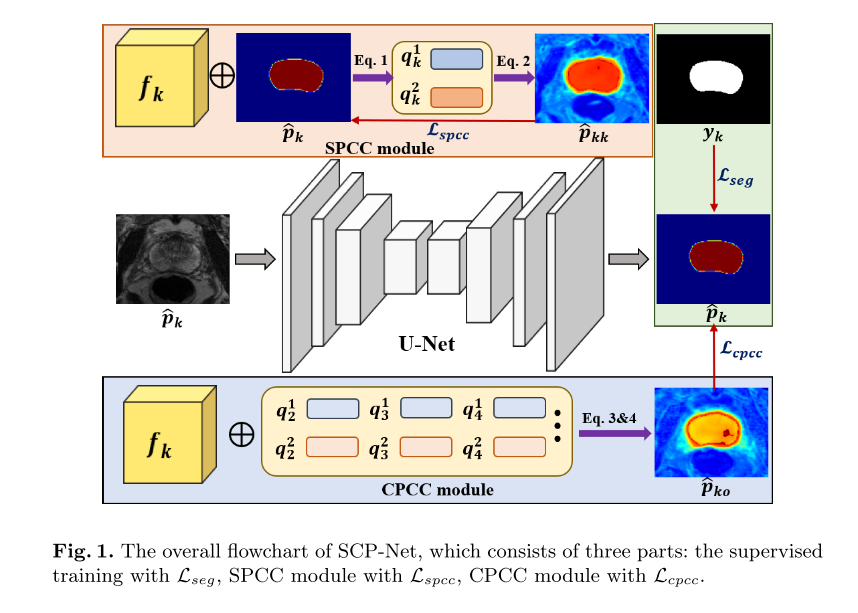
2.1 自交原型预测
分割中的原型是指从特定对象或类中捕获某些像素级特征的共同特征的聚合表示。 设 p k i c p_{ki}^{c} pkic表示像素i属于C类的概率, f k ∈ R D × H × W f_{k}\in\mathbb{R}^{D\times H\times W} fk∈RD×H×W表示样本k的特征映射。 按类划分的原型 q k c q_{k}^{\mathbf{c}} qkc定义如下:
q k c = ∑ i p k c ( i ) ⋅ f k ( i ) ∑ i p k c ( i ) q_k^c=\frac{\sum_ip_k^c(i)\cdot f_k(i)}{\sum_ip_k^c(i)} qkc=∑ipkc(i)∑ipkc(i)⋅fk(i)
设 B B B表示批大小。 在迭代训练过程中,一个小批包含样本 k = 1 k=1 k=1的 B × C B\times C B×C原型和指数 j = 2 , 3 , ⋯ , B j=2,3,\cdots,B j=2,3,⋯,B的其他样本。然后根据Selfaware原型 q k c q_{k}^{c} qkc或交叉样本原型 q j c q_{j}^{c} qjc计算特征相似度,形成多个分割概率矩阵。 具体而言, s ^ k k c \hat{s}_{kk}^{c} s^kkc是通过计算特征映射 f k f_{k} fk与原型向量 q k c q_{\boldsymbol{k}}^{c} qkc之间的余弦相似度作为公式2而得到的自感知原型相似度映射。
s ^ k k c = f k ⋅ q k c ∥ f k ∥ ⋅ ∥ q k c ∥ \hat{s}_{kk}^{c}=\frac{f_{k}\cdot q_{k}^{c}}{\|f_{k}\|\cdot\|q_{k}^{c}\|} s^kkc=∥fk∥⋅∥qkc∥fk⋅qkc
然后,利用softmax函数生成基于 s ^ k k ∈ R C × H × W \hat{s}_{kk}\in\mathbb{R}^{C\times H\times W} s^kk∈RC×H×W的自感知概率预测 p ^ k k ∈ R C × H × W \hat{p}_{kk}\in\mathbb{R}^{C\times H\times W} p^kk∈RC×H×W。由于 q k c q_{k}^{c} qkc在样本 k k k中聚合,可以使 f k f_{k} fk与更多的同源特征对齐,保证了预测的类内一致性。同样,我们可以得到式3下的B−1跨样本原型相似度映射 s ^ k j c \hat{s}_{kj}^{c} s^kjc:
s ^ k j c = f k ⋅ q j c ∥ f k ∥ ⋅ ∥ q j c ∥ \hat{s}_{kj}^c=\frac{f_k\cdot\boldsymbol{q}_j^c}{\|f_k\|\cdot\left\|q_j^c\right\|} s^kjc=∥fk∥⋅ qjc fk⋅qjc
这一步确保特征是相关联的,并且信息是以跨图像的方式交换的。 为了提高预测的可靠性,我们考虑了多重相似性估计 s ^ k j ∈ R C × H × W \hat{s}_{kj}\in\mathbb{R}^{C\times H\times W} s^kj∈RC×H×W,并将其综合得到跨样本概率预测 p ^ k o ∈ R C × H × W \hat{p}_{ko}\in\mathbb{R}^{C\times H\times W} p^ko∈RC×H×W:
p ^ k o c = ∑ j = 2 B e s ^ k j c ∑ c ∑ j = 2 B e s ^ k j c \hat{p}_{ko}^c=\frac{\sum_{j=2}^Be^{\hat{s}_{kj}^c}}{\sum_{c}\sum_{j=2}^Be^{\hat{s}_{kj}^c}} p^koc=∑c∑j=2Bes^kjc∑j=2Bes^kjc
2.2 典型预测不确定性
为了有效地评估半监督环境下的预测一致性和训练稳定性,我们提出了一种基于相似矩阵 s ^ k k \hat{s}_{kk} s^kk和 s ^ k j \hat{s}_{kj} s^kj的原型预测不确定性估计方法。 首先,我们通过Argmax运算和一热编码运算生成B个二进制表示的掩码 m ^ k n ∈ R C × H × W \hat{m}_{kn}\in\mathbb{R}^{C\times H\times W} m^kn∈RC×H×W,其中 n = 1 , 2 , ⋯ , B n=1,2,\cdots,B n=1,2,⋯,B。然后,我们将所有的掩码 m ^ k n \hat{m}_{kn} m^kn求和并除以B,得到归一化概率 p ^ n o r m \hat{p}_{norm} p^norm为:
p ^ n o r m c = ∑ n = 1 B m ^ k n c B \hat{p}_{norm}^{c}=\frac{\sum_{n=1}^{B}\hat{m}_{kn}^{c}}{B} p^normc=B∑n=1Bm^knc
由 p ^ n o r m \hat{p}_{norm} p^norm估计一个归一化熵,记为 e k ∈ R H × W e_{k}\in\mathbb{R}^{H\times W} ek∈RH×W:
e k = − 1 log ( C ) ∑ c = 1 C p ^ n o r m c log p ^ n o r m c e_k=-\frac{1}{\log(C)}\sum_{c=1}^C\hat{p}_{norm}^c\log\hat{p}_{norm}^c ek=−log(C)1c=1∑Cp^normclogp^normc
其中 e k e_k ek是多个原型预测的总体置信度,更高的熵等于更多的预测不确定性。 然后,我们使用EK来调整标记和未标记样本的像素加权,这将在下一小节中阐述。
2.3 无监督原型一致性约束
为了提高一致性学习中的预测多样性和训练有效性,减轻 p ^ k k \hat{p}_{kk} p^kk和 p ^ k j \hat{p}_{kj} p^kj中噪声预测的负面影响,我们在SCP-Net中提出了两种无监督的原型一致性约束(PCC),利用了自感知原型预测 p ^ k k \hat{p}_{kk} p^kk、跨样本原型预测 p ^ k j \hat{p}_{kj} p^kj以及相应的不确定性估计 e k e_k ek。
自感知原型一致性约束(SPCC)为了提高分割预测的类内紧凑性,提出了一种将 p ^ k k \hat{p}_{kk} p^kk作为伪标记监督的SPCC方法。 因此,SPCC的损失函数公式化为:
L s p c c = 1 C × H × W ∑ i = 1 H × W ∑ c = 1 C ∥ p ^ k k c ( i ) − p k c ( i ) ∥ 2 \mathcal{L}_{spcc}=\frac{1}{C\times H\times W}\sum_{i=1}^{H\times W}\sum_{c=1}^{C}\left\|\hat{p}_{kk}^{c}(i)-p_{k}^{c}(i)\right\|_{2} Lspcc=C×H×W1i=1∑H×Wc=1∑C∥p^kkc(i)−pkc(i)∥2
交叉感知的原型一致性约束(CPCC) 为了从其他训练样本中获得可靠的知识,我们提出了CPCC的双重加权方法。
首先,我们将不确定性估计 e k e_k ek考虑在内,它反映了预测的稳定性。 e k e_k ek的值越高,表明具有较大不确定性的伪标签可能越容易出错。然而,这些区域为分割性能提供了有价值的信息。为了减少可疑伪标签的影响,并在训练过程中调整这些关键监督信号的贡献,我们通过设置权重 w 1 k i = 1 − e k i w_{1ki}=1-e_{ki} w1ki=1−eki将 e k e_k ek纳入CPCC中。其次,我们将自知的概率预测 p ^ k k \hat{p}_{kk} p^kk引入CPCC模块。具体来说,我们沿着c类计算 p ^ k k \hat{p}_{kk} p^kk的最大值,称为自我意识到的信心权重 w 2 k i w_{2ki} w2ki:
w 2 k i = max c p ^ k k c ( i ) w_{2ki}=\max_c\hat{p}_{kk}^c(i) w2ki=cmaxp^kkc(i)
w 2 k w_{2k} w2k可以进一步提高CPCC的可靠性。 因此,在交叉感知原型预测 p ^ k o \hat{p}_{ko} p^ko和 p ^ k \hat{p}_{k} p^k之间计算CPCC的优化函数:
L c p c c = 1 C × H × W ∑ i = 1 H × W ∑ c = 1 C w 1 k i ⋅ w 2 k i ⋅ ∥ p ^ k o c ( i ) − p k c ( i ) ∥ 2 {\cal L}_{cpcc}=\frac{1}{C\times H\times W}\sum_{i=1}^{H\times W}\sum_{c=1}^{C}w_{1ki}\cdot w_{2ki}\cdot\left\|\hat{p}_{ko}^{c}(i)-p_{k}^{c}(i)\right\|_{2} Lcpcc=C×H×W1i=1∑H×Wc=1∑Cw1ki⋅w2ki⋅∥p^koc(i)−pkc(i)∥2
SCP-Net的损失函数我们使用交叉熵损失 L c e \mathcal{L}_{ce} Lce和骰子损失 L D i c e \mathcal{L}_{Dice} LDice的结合来监督标记集的训练过程[9],定义为:
L s e g = L c e ( p ^ k , y k ) + L D i c e ( p ^ k , y k ) \mathcal L_{seg}=\mathcal L_{ce}(\hat{p}_{k},y_{k})+\mathcal L_{Dice}(\hat{p}_{k},y_{k}) Lseg=Lce(p^k,yk)+LDice(p^k,yk)
对于有标记数据和无标记数据,我们利用 L s p c c \mathcal{L}_{spcc} Lspcc和 L c p c c \mathcal{L}_{cpcc} Lcpcc为网络训练提供无监督一致性约束,并挖掘有价值的无标记知识。 概括起来,SCP-Net的总体损失函数是监督损失和无监督一致性损失的组合,其表述为:
L t o t a l = ∑ k = 1 N l L s e g ( p ^ k , y k ) + λ ∑ k = 1 N l + N u ( L s p c c ( p ^ k , p ^ k k ) + L c p c c ( p ^ k , p ^ k o ) ) \mathcal{L}_{total}=\sum\limits_{k=1}^{N_l}\mathcal{L}_{seg}(\hat{p}_k,y_k)+\lambda\sum\limits_{k=1}^{N_l+N_u}(\mathcal{L}_{spcc}(\hat{p}_k,\hat{p}_{kk})+\mathcal{L}_{cpcc}(\hat{p}_k,\hat{p}_{ko})) Ltotal=k=1∑NlLseg(p^k,yk)+λk=1∑Nl+Nu(Lspcc(p^k,p^kk)+Lcpcc(p^k,p^ko))
λ ( t ) = 0.1 ⋅ e − 5 ( 1 − t / t m a x ) 2 \lambda\left(t\right)=0.1\cdot e^{-5\left(1-t/t_{max}\right)^{2}} λ(t)=0.1⋅e−5(1−t/tmax)2是使用时间相关的高斯预热函数[10]来平衡监督损失和非监督损失的权重。 T表示当前的训练迭代,而 t m a x t_{max} tmax是总的迭代。
知乎总结:
SPCC
自感知原型一致性约束(SPCC)旨在增强分割预测的类内紧密性。它利用自我知原型预测作为伪标签进行监督。通过使用自感知原型,该方法能够在样本本身上对特征进行更准确的对齐,从而确保预测的类内一致性。通过引入这个约束,模型可以更好地学习到类别内部的共性特征,提高分割性能。
CPCC
跨样本感知原型一致性约束(CPCC)旨在从其他训练样本中获得可靠的知识。它采用双重加权方法,通过考虑不确定性估计和自感知概率预测来调整约束的贡献。
首先,使用不确定性估计来降低可疑伪标签的影响,减少这些具有较大不确定性的区域在训练中的权重。其次,引入自感知概率预测,计算在特定类别上的最大值作为权重,进一步增强CPCC的可靠性。通过这种双重加权方法,CPCC能够更好地利用跨样本的原型预测来提升分割模型的性能和稳定性。
3 实验与结果
3.1 数据集和评价指标
我们在两个公共基准上验证了我们方法的有效性,即自动心脏诊断挑战1(ACDC)数据集[11]和前列腺MR图像分割挑战2(Promese12)数据集[12]。 ACDC数据集包含来自100名受试者的200个注释短轴心脏电影MRI扫描。 所有扫描随机分为140个训练扫描、20个验证扫描和40个测试扫描,遵循之前的工作[13]。 PROMERE12数据集包含50幅T2加权MRI扫描,分为35个训练案例、5个验证案例和10个测试案例。 所有的3D扫描都被转换成2D切片。 然后,将每个切片的大小调整为256×256,并将其归一化为[0,1]。 为了评价半监督分割的性能,我们使用了两个常用的评价指标:骰子相似系数(DSC)和平均对称曲面距离(ASSD)。
3.2 实施细节
我们的方法采用U-Net[14]作为基线。 我们使用初始学习率为0.1的随机梯度下降(SGD)优化器,并在训练过程中应用“聚”学习率策略更新学习率。 批大小设置为24。 每批包括12个标记切片和12个未标记切片。 为了减少过拟合,我们采用随机翻转和随机旋转来增加数据。 所有对比实验和烧蚀实验都遵循相同的设置,为了公平的比较,我们对所有对比实验和烧蚀实验都使用相同的实验设置。 所有框架都使用PyTorch实现,并在一台具有3.0GHz CPU、128 GB RAM和4个NVIDIA GeForce RTX 3090 GPU的计算机上执行。
3.3 与其他方法的比较
为了验证SCPNET的有效性,我们将它与7种最先进的半监督分割方法和全监督(100%标记率)有限监督(10%标记率)基线方法进行了比较。 ACDC数据集的定量分析结果如表1所示。
在RV、MYO和LV的DSC上,SCP-NET显著优于有限监督基线,分别为7.02%、6.13%和6.32%。
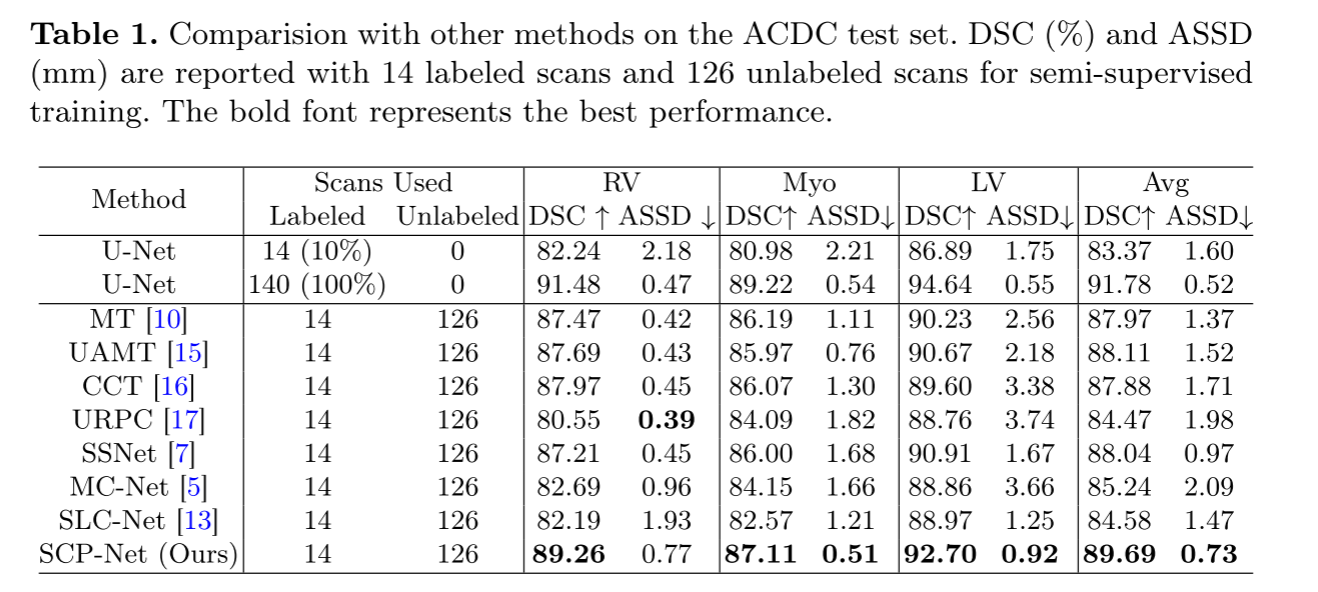
SCP-NET实现了与完全监督基线相比较的DSC和ASSD。 (89.69%对91.78,0.73%对0.52)。 与其它方法相比,SCP-NET获得了最好的DSC和ASSD,分别比第二好的指标提高了1.58%和0.24%。
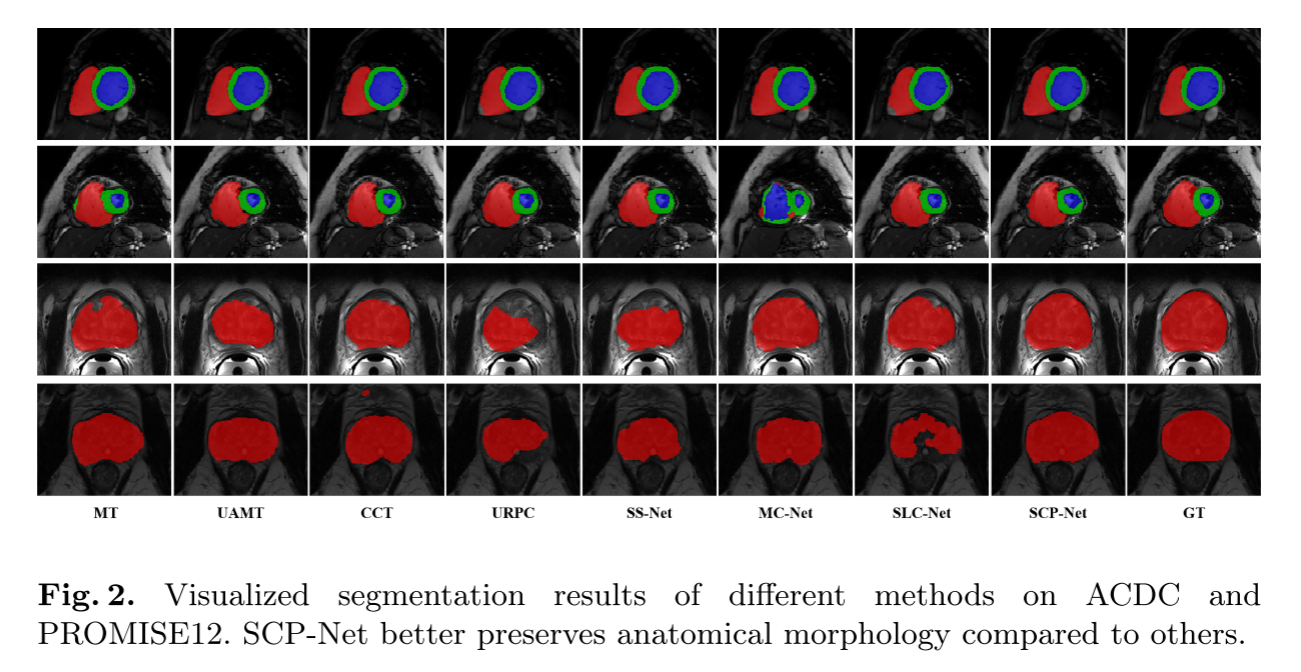
在此基础上,给出了几个ACDC数据集在图中的可视化分割实例 2. SCP-Net对RV、MYO和LV类的分割结果一致且准确,证明了无监督原型一致性约束有效地提取了有价值的未标记信息,提高了分割性能。
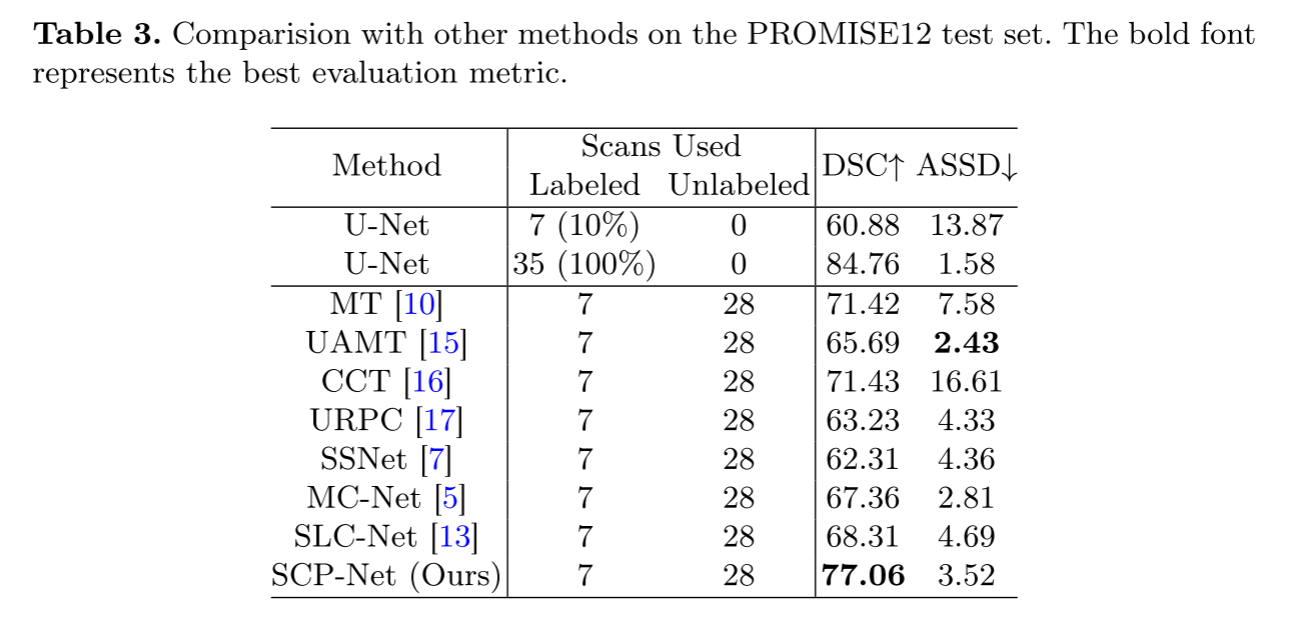
补充材料表3报告了前列腺节段的定量结果。 我们还分别以10%的标记率和100%的标记率进行有限监督训练和完全监督训练。 SCP-NET在DSC和ASSD上分别超过限制监督基线16.18%和10.35%。
另外,SCP-NET的DSC最高,为77.06%,比第二好的CCT提高了5.63%。
所有的改进都表明,SPCC和CPCC有利于利用未标记信息。 我们还在最后两行图中可视化了一些前列腺分割示例 2. 我们可以观察到SCP-NET产生解剖学上可信的前列腺分割结果。
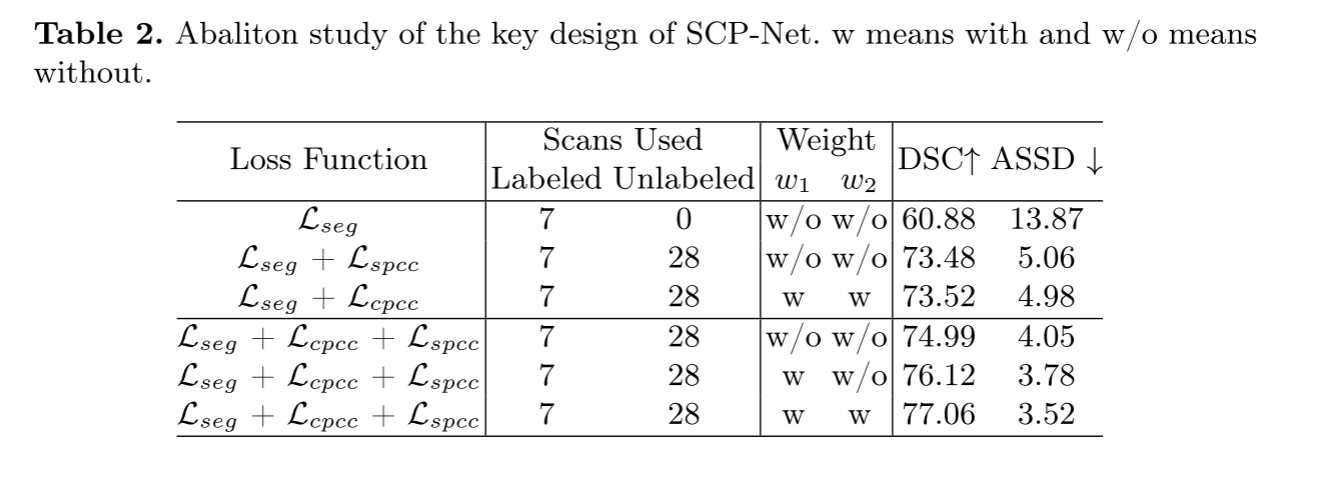
3.4 消融研究
为了验证SCPNET关键设计的有效性,我们在Promise12数据集上通过逐步增加损耗分量进行烧蚀研究。 表2报告了消融结果的结果。 结果表明,SPCC和CPCC的设计都提高了前三行半监督分割的性能,表明PCC能够从图像本身和其他图像中提取有价值的信息,非常适合于半监督分割。 我们还可视化了图不同结构的原型预测PKK和PKO 3. 这些预测结果与实际情况一致,并表现出类内紧凑性和类间差异,验证了PCC对半监督分割提供了有效的监督。 在最后三行,逐渐提高的性能验证了CPCC中预测不确定性W1和自我感知置信度W2的集成提高了一致性训练的可靠性和稳定性。
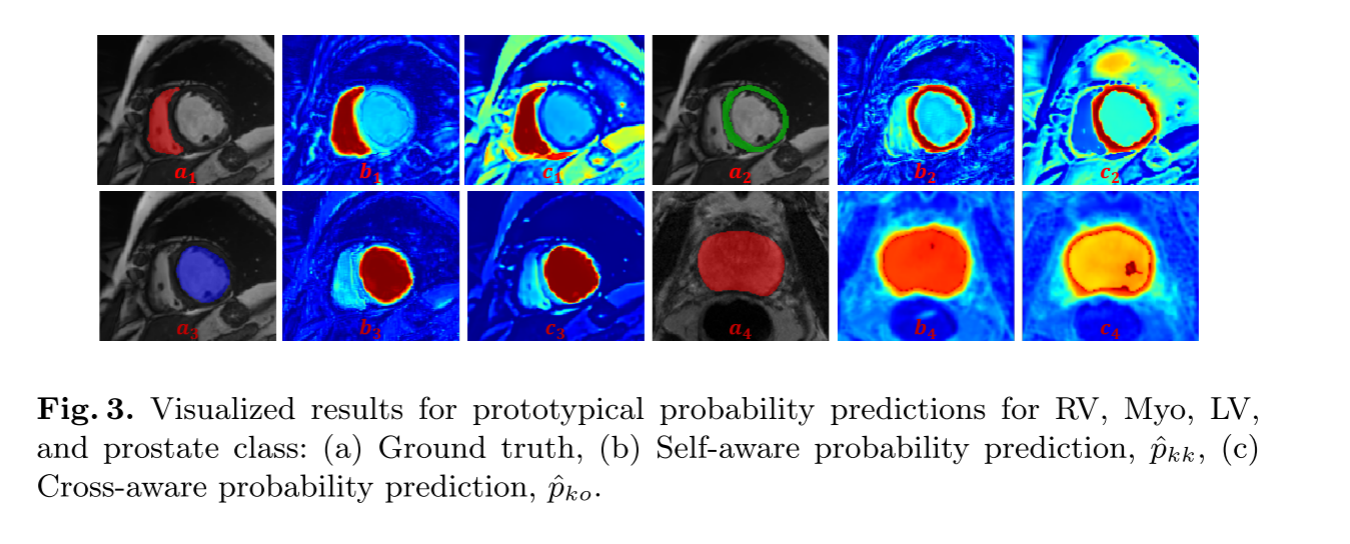
4. 总结
总之,我们提出的SCP-Net利用了自感知和交叉样本原型一致性学习,成功地解决了半监督一致性学习中预测多样性和训练有效性的挑战。 SPCC提高了伪标记的类内紧性。 CPCC的双损失重加权方法提高了模型的可靠性。 良好的分割性能表明,在有限的标注数据下,SCP-NET有效地利用了有用的未标记信息来提高分割性能。 展望未来,我们的重点将是研究学习可适应数量的原型的可行性,这些原型可以有效地处理不同级别的类别复杂度。 通过这样做,我们期望增强原型预测的质量并改善整体性能。
MICCAI 2023 | SCP-Net: 基于一致性学习的半监督医学图像分割方法 - 知乎 (zhihu.com)
![软件项目管理第4版课后习题[附解析]第一章](https://img-blog.csdnimg.cn/20210614233443926.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQ0MDg0Nzg0,size_16,color_FFFFFF,t_70#pic_center)