把一棵树转化成一个序列有三种方法：

dfs序

dfn序（时间戳）

欧拉序

关于这三者的区别，参考这篇博客，讲的超级好！

重谈DFS序、时间戳和欧拉序 - Seaway-Fu - 博客园 (cnblogs.com)

题意：

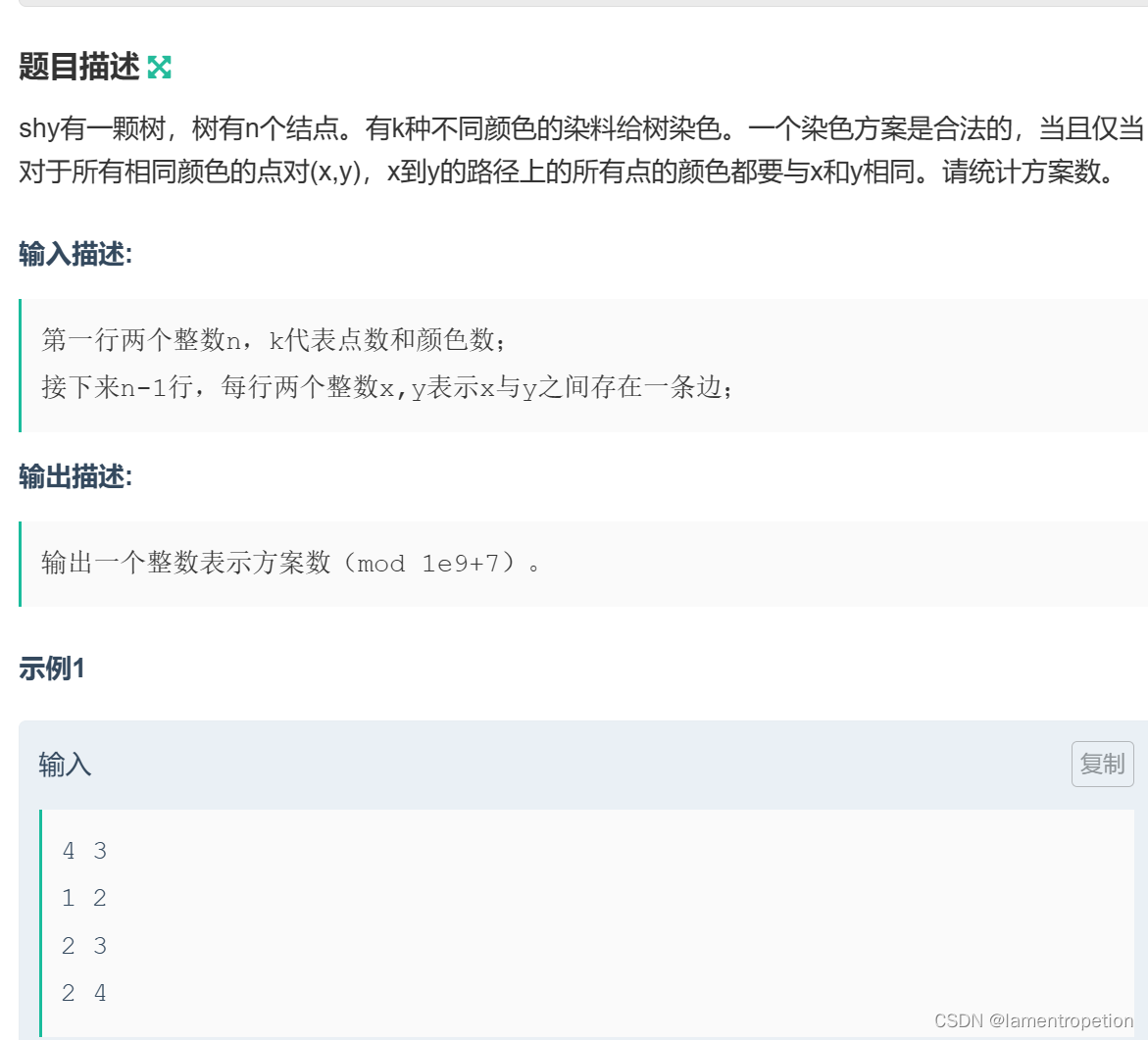
思路：

看起来是个树形DP，事实上并不是

考虑把整棵树转化成一个序列

为什么要这么转化：把一棵树转化为序列之后，树上很多东西都可以用DS维护了

如果我们用dfn序来表示这棵树，并且按dfn序来一个一个点涂色的话，我们就可以把问题从树上转化到链上，问题也许会简单许多。

我们会发现，如果我们按dfn序涂色，在涂每一个点之前，他的父亲祖父等祖先节点肯定都已经先涂过了（这些点的dfn序都比当前点小），他的兄弟节点（也包括各种或近或远的“堂兄弟”节点）和兄弟节点的子树也许也涂过一些。涂这个点无非是两种选择：涂一种新的颜色，或者涂一种已经用过的颜色。涂一种新的颜色自然是没用过的颜色都可以。而涂一种已经用过的颜色的话，这个点的颜色必须和他父亲的颜色一样，因为这个点到之前的所有点的路径都是要经过它父亲的，如果他和父亲不同色，他和他同色那个点的路径上就不可能所有点颜色都一样，至少他父亲就是不同的。也就是说涂一种已经用过的颜色其实只有一种方案——和父亲相同。

所以我们可以在它的dfn序上DP

由于有限制：只能用K种颜色

因此设dp[i][j]为前i个点，已经用了j种颜色的方案数

转移就很显然了：

Code：

#include <bits/stdc++.h>#define int long longusing namespace std;const int mxn=3e2+10;
const int mod=1e9+7;int N,K;
int dp[mxn][mxn];void solve(){cin>>N>>K;dp[1][1]=K;for(int i=2;i<=N;i++){for(int j=1;j<=K;j++){dp[i][j]=(dp[i-1][j]+dp[i-1][j-1]*(K-j+1)%mod)%mod;}}int ans=0;for(int j=1;j<=K;j++) ans=(ans+dp[N][j])%mod;cout<<ans<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;while(__--)solve();return 0;
}