对空气质量进行预测
我们可以通过对以往数据的分析,建立模型,然后将这种模式去应用于未知的数据,进而预测结果。
数据转换
因为对于模型来说,内部进行的都是数学运算,故在进行建模之前,我们需要将类别变量转换为离散变量。
data['Coastal'] = data['Coastal'].map({'是':1, '否':0})
基模型
首先建立一个不做任何处理的基模型,后续的操作,可以在此基础上进行改进。
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_splitx = data.drop(['City','AQI'], axis=1) #删除城市以及AQI两列
y = data['AQI']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random=0)lr = LinearRegression()
lr.fit(x_train, y_train)
print('训练集R^2值:', lr.score(x_train, y_train))
print('测试集R^2值:', lr.score(x_test, y_test))
训练集R^2值:0.4538897765064036
测试集R^2值:0.40407705623832957
线性回归预测结果
y_hat = lr.predict(x_test)
plt.figure(figsize=(15,5))
plt.plot(y_test.values, '-r', label='真实值', marker='o')
plt.plot(y_hat, '-g', label='预测值', marker='D')
plt.legend(loc='upper left')
plt.title('线性回归预测结果', fontsize=20)

特征选择
上面我们使用所有可能的原始数据作为特征,建立模型,然而,特征并非越多越好,有些对模型质量没有什么改善的特征,可以进行删除,以提高模型质量。
RFECV模型
from sklearn.feature_selection import RFECV#estimator:要操作的模型
#step:每次删除的变量数
#cv:使用的交叉验证折数(就是把数据分成几份)
#n_jobs:并发的数量
#scoring:评估方式rfecv = RFECV(estimator=lr, step=1, cv=5, n_job=1, scoring='r2')
rfecv.fit(x_train, y_train)
#返回经过选择之后,剩余的特征数量
print(rfecv.n_features_)
#返回经过特征选择后,使用缩减特征训练后的模型
print(rfecv.estimator_)
#返回每个特征的等级,数值越小,特征越重要
print(rfecv.ranking_)
#返回布尔数组,用来表示特征是否被选择
print(rfecv.support_)
#返回对应数量特征时,模型交叉验证的评分
print(rfecv.grid_scores_)

通过结果可知,我们可以删除两个特征
#绘制特征数量
plt.plot(range(1, len(rfecv.grid_scores_)+1), rfecv.grid_scores_, marker='o')
plt.xlabel('特征数量')
plt.ylabel('交叉验证R^2值')

对测试集应用这种特征选择,进行测试,获取测试结果。
print('剔除的变量:',x_train.columns[~rfecv.support_])
x_train_eli = rfecv.transform(x_train)
x_test_eli = rfecv.transform(x_test)
print(rfecv.estimator_.score(X_train_eli, y_train))
print(rfecv.estimator_.score(X_test_eli, y_test))

可以发现,经过特征选择后,使用剩余8个特征训练的模型,与之前模型表现上几乎没有变化,对拟合目标没有什么帮助。
异常值处理
如果数据中存在异常值,很有可能会影响模型的效果,因此在建模时,有必要对异常值进行处理。
使用临界值替换
可以依据箱线图判断离群点的原则探索异常值,使用临界值替换。
#Coastal是类别变量,映射为离散变量,不会有异常值.
for col in X.columns.drop('Coastal'):if pd.api.types.is_numeric_dtype(X_train[col]): #判断是否为数值类型quartile = np.quantile(X_train[col], [0.25, 0.75]) #取四分之一分位和四分之三分位IQR = quartile[1]-quartile[0] #四分之三分位数减去四分之一分位数lower = quartile[0]-1.5*IQRupper = quartile[1]+1.5*IQR#赋值X_train[col][X_train[col] < lower] = lower X_train[col][X_train[col] > upper] = upperX_test[col][X_test[col] < lower] = lowerX_test[col][X_test[col] > upper] = upper
去除异常值后,我们使用新的训练集与测试集来评估模型的效果
lr.fit(X_train,y_train)
print(lr.score(X_train,y_train))
print(lr.score(X_test,y_test))
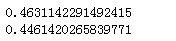
可以看出去除异常值后,结果有轻微的改进。
分箱操作
注意:分箱后,我们不能将每个区间映射为离散数值,而是应当使用One-Hot编码。
from sklearn.preprocessing import KBinsDiscretizer#KBinsDiscretizer K个分箱的离散器,用于将数值(通常是连续变量)变量进行区间离散化操作
#n_bin:分箱(区间)个数
#encode:离散化编码方式,分为:onehot、onehot-dense与ordinal
# onehot:使用独热编码,返回稀疏矩阵
# onehot-dense:使用独热编码,返回稠密矩阵
# ordinal:使用序数编码(0,1,2……)
#strategy:分箱的方式,分为:uniform、quantile、kmeans
# uniform:每个区间的长度范围大致相同
# quantile:每个区间包含的元素个数大致相同
# kmeans:使用一维kmeans方式进行分箱k = KBinsDiscretizer(n_bins=[4, 5, 14, 6], encode='onehot-dense', strategy='uniform')
#定义离散化的特征
discretize = ['Longitude', 'Temperature', 'Precipitation', 'Latitude']r = k.fit_transform(X_train_eli[discretize])
r = pd.DataFrame(r, index=X_train_eli.index)
#获取除离散化特征之外的其他特征
X_train_dis = X_train_eli.drop(discretize, axis=1)
#将离散化后的特征与其他特征进行重新组合
X_train_dis = pd.concat([X_train_dis, r], axis=1)
#对测试集进行同样的离散化操作
r = pd.DataFrame(k.transform(X_test_eli[discretize]), index=X_test_eli.index)
X_test_dis = X_test_eli.drop(discretize, axis=1)
X_test_dis = pd.concat([X_test_dis, r], axis=1)
#查看转换之后的格式
display(X_train_dis.head())

训练转换后的数据
lr.fit(x_train_dis, y_train)
print(lr.score(x_train_dis, y_train))
print(lr.score(x_test_dis, y_train))
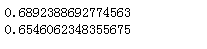
分箱操作后,可以看到模型效果有了进步。