使用python绘制任意函数图像
##原创文章不易,望点赞转发收藏三连
效果展示

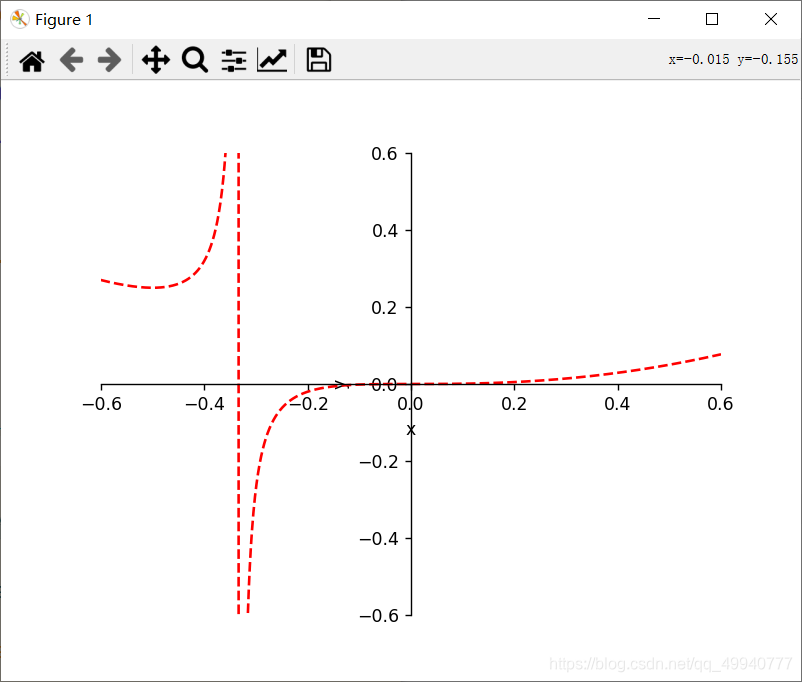
y = (sinx)/x
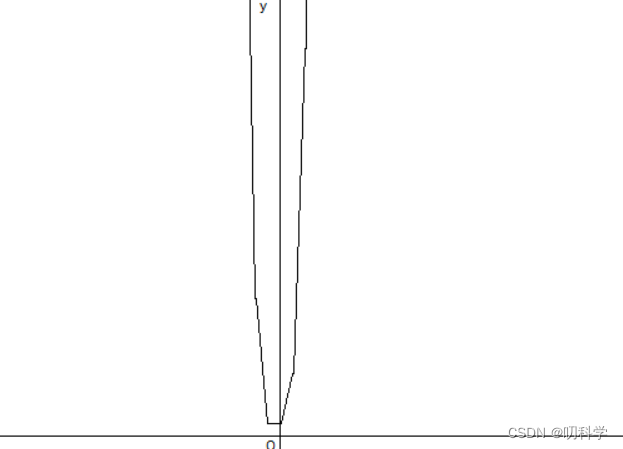
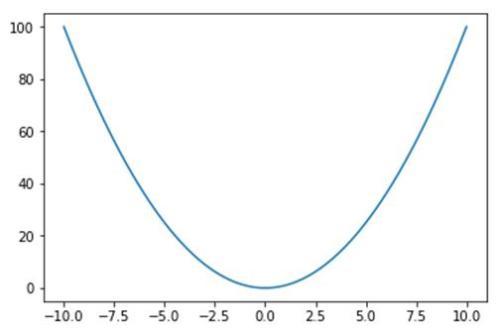
y = x4+x3+x^2+1


y=-x^2
文末还会展示一些实例图片
引入需要的库
我们使用如下库
import turtle as t
import math
这两个库的用法也是本项目的核心
其中基本语法不再赘述
大家可以网络搜索
核心算法
我们假设像素点为坐标点,通过goto(x,y)与y,x的函数关系进行找点
通过penup().pendown()连接个点,视觉上像素点的连线几乎为曲线
当然,可以通过仅仅画点保证准确度
绘画坐标系
坐标系的绘制不是难事,就是麻烦,我已经经过尝试,给出以下数据,方便大家使用
t.screensize(800,800,"white")
t.hideturtle()
t.speed(0)
t.pendown()
t.goto(0,0)
t.forward(800)
t.left(90)
t.goto(0,0)
t.forward(800)
t.left(90)
t.goto(0,0)
t.forward(800)
t.left(90)
t.goto(0,0)
t.forward(800)
t.left(90)
t.penup()
t.goto(-10,-15)
t.write("O")
t.goto(350,-15)
t.write("x")
t.goto(-15,337)
t.write("y")
基本设置
我们再画图像之前要初始化x的位置,避免画到画布外,否则会报错
之后处理y时,也要注意这一点
另外,可以设置曲线粗细和绘画速度
粗细1–>n变粗
速度1–>10->0变快
n = int(input(r"输入需要放大的倍数:"))
x = int((-350)/n)
t.pensize(1)
t.speed(10)
while pass:pass
处理函数关系
首先两个确定:
1.确定函数解析式,要符合python语法
2.确定定义域的补集合
然后避免两点:
1.避免x的取值超出定义域,出现MATHS ERROR
2.避免y超出范围,导致ERROE
再注意两个近似:
1.可以每个点向前画一个坐标,近似于点
2.pendown()下的goto()连接点,近似于曲线
还有两个选择:
1.penup()的注释取消后,将t.penup()加入代码,可以之画点不连线
2.math库可以丰富函数类型
while x <= int((350)/n):if x!=0: #定义域的反域y = m.sin(x)/x #函数解析式if y>=-350 and y<=350:t.goto(n*x,y*n)t.pendown()t.forward(1)#t.penup()x+=1
如果实在不清楚定义域或者表示起来不方便
也可以采用try-except结构自动处理
while pass:try:y = math.sin(x)/xexcept:#breakpass ###根据需要选择,建议直接passpass
最后别忘了title库结尾的title.done()
展示源代码
import turtle as t
import math as m
t.screensize(800,800,"white")
t.hideturtle()
t.speed(0)
t.pendown()
t.goto(0,0)
t.forward(800)
t.left(90)
t.goto(0,0)
t.forward(800)
t.left(90)
t.goto(0,0)
t.forward(800)
t.left(90)
t.goto(0,0)
t.forward(800)
t.left(90)
t.penup()
t.goto(-10,-15)
t.write("O")
t.goto(350,-15)
t.write("x")
t.goto(-15,337)
t.write("y")n = int(input(r"输入需要放大的倍数:"))
x = int((-350)/n)
t.pensize(1)
t.speed(10)
while x <= int((350)/n):if x!=0: #定义域的反域y = m.sin(x)/x #函数解析式if y>=-350 and y<=350:t.goto(n*x,y*n)t.pendown()t.forward(1)#t.penup()x+=1
t.down()图片展示
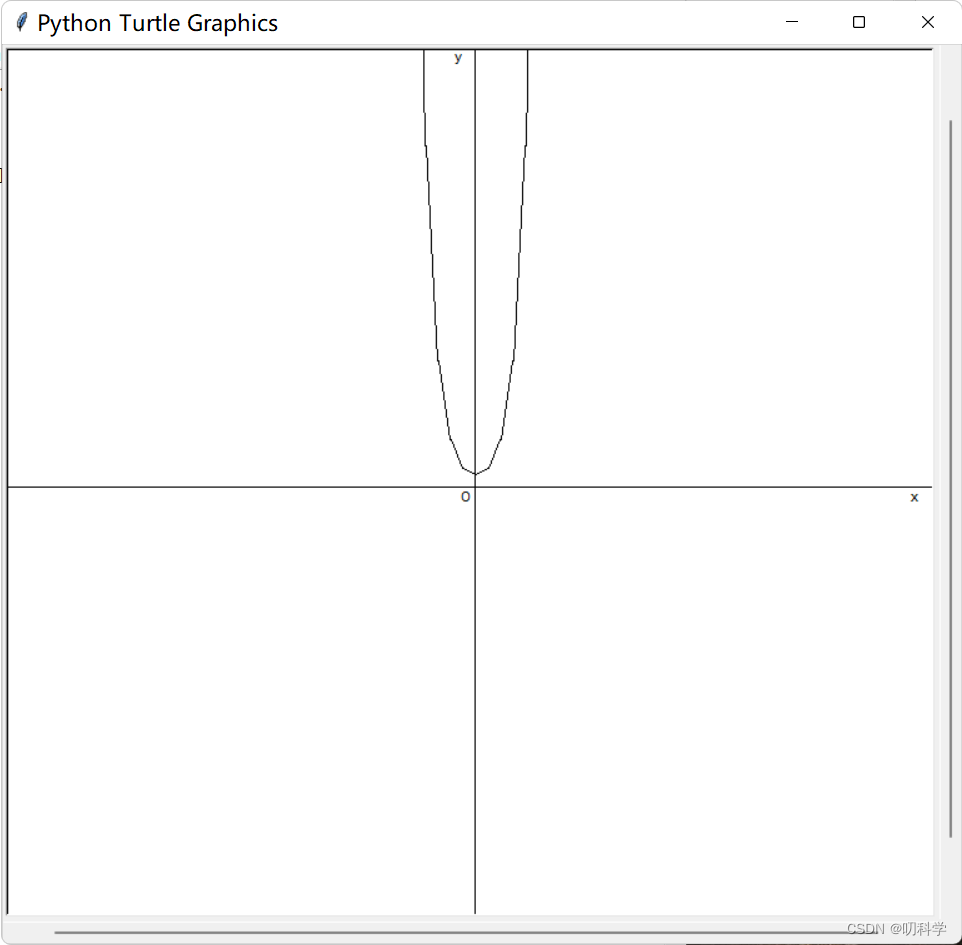
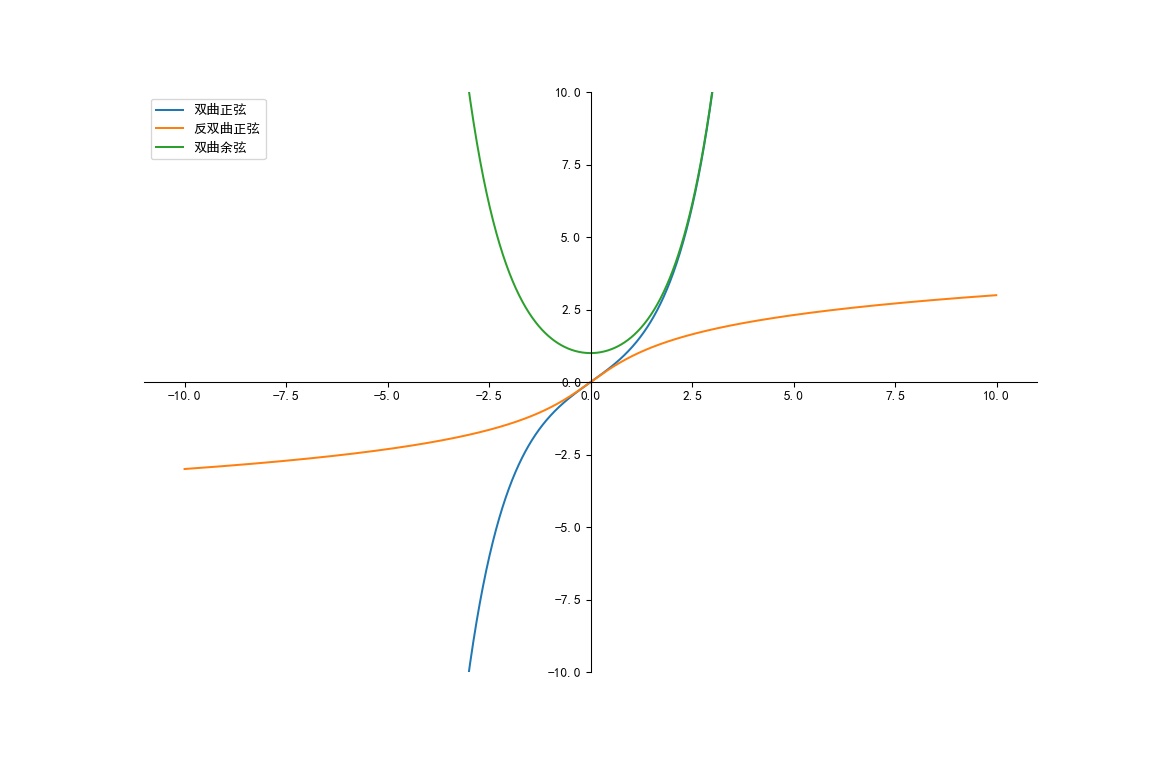
双曲正弦
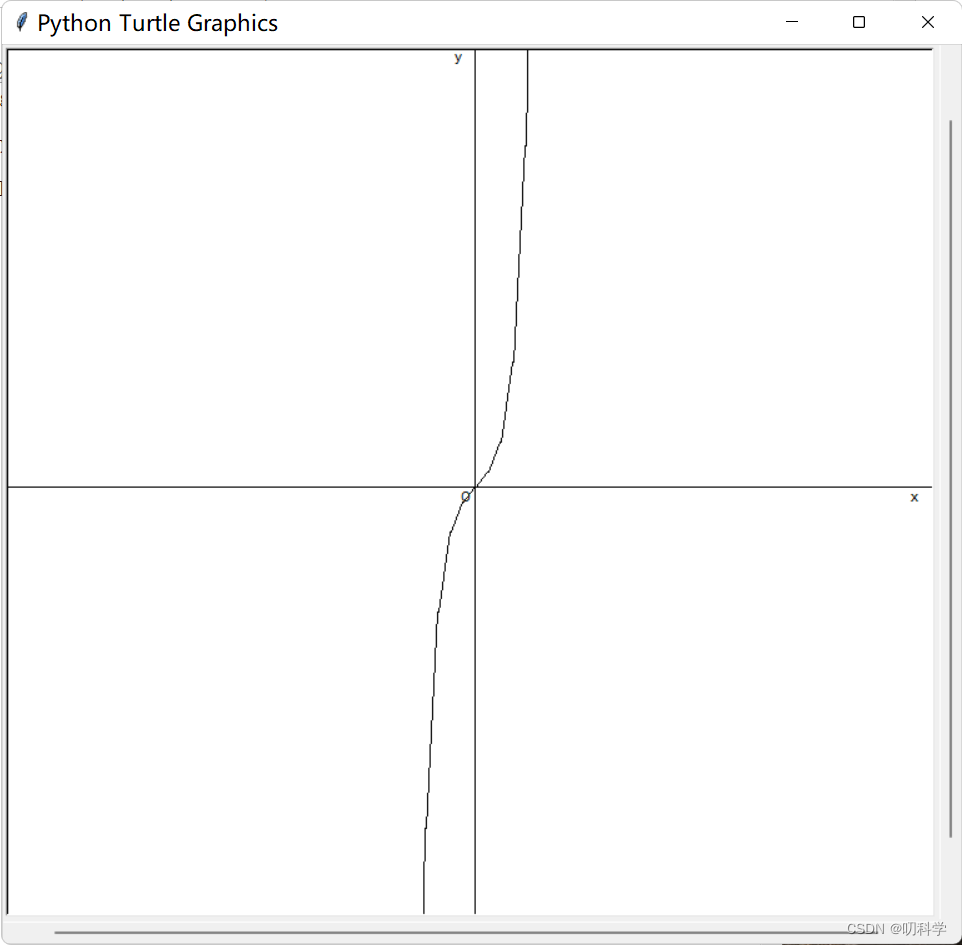
双曲余弦
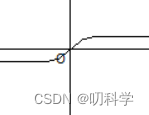
双曲正切(原点附近)
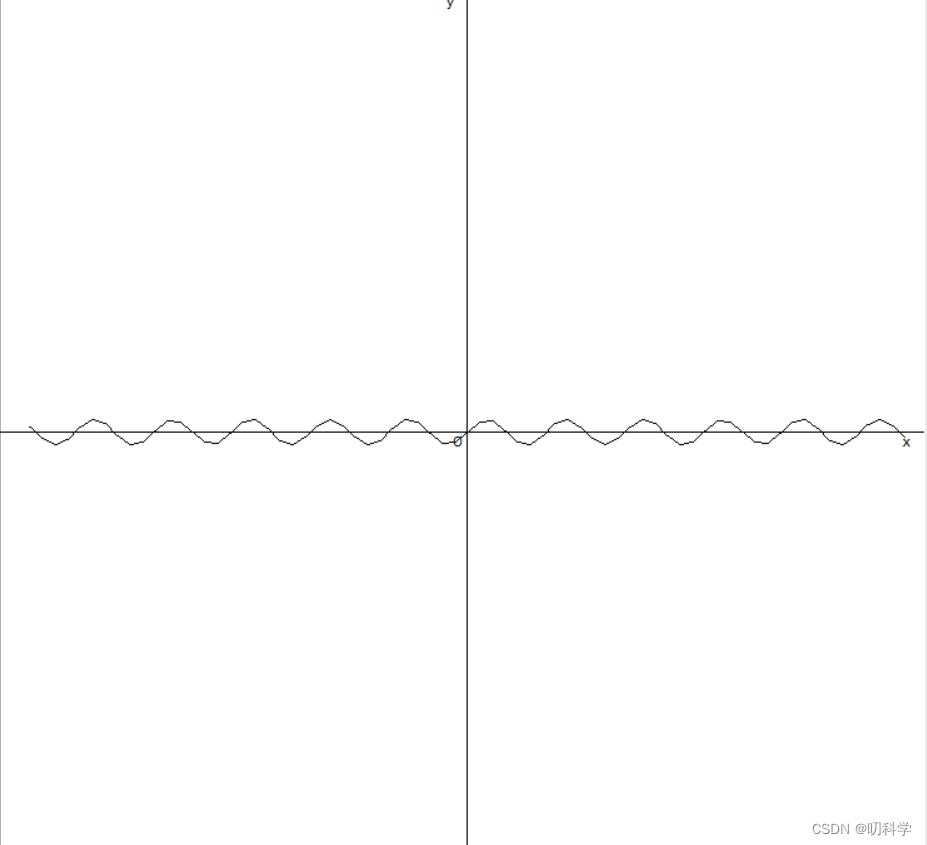
正弦
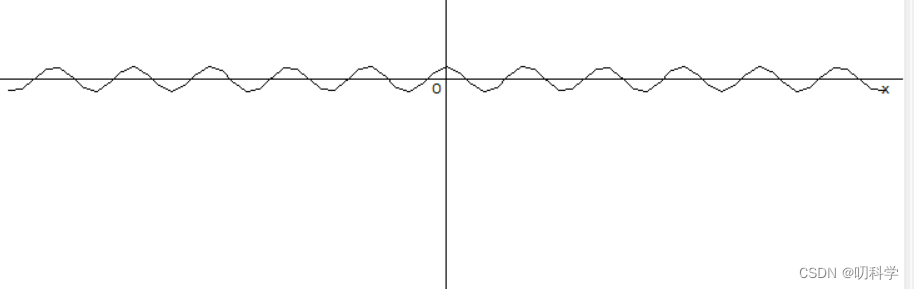
余弦