课程链接: 清华大学驭风计划
代码仓库:Victor94-king/MachineLearning: MachineLearning basic introduction (github.com)
驭风计划是由清华大学老师教授的,其分为四门课,包括: 机器学习(张敏教授) , 深度学习(胡晓林教授), 计算机语言(刘知远教授) 以及数据结构与算法(邓俊辉教授)。本人是综合成绩第一名,除了数据结构与算法其他单科均为第一名。代码和报告均为本人自己实现,由于篇幅限制,只展示任务布置以及关键代码,如果需要报告或者代码可以私聊博主
机器学习部分授课老师为胡晓林教授,主要主要通过介绍回归模型,多层感知机,CNN,优化器,图像分割,RNN & LSTM 以及生成式模型入门深度学习
有任何疑问或者问题,也欢迎私信博主,大家可以相互讨论交流哟~~
任务介绍
本次案例中,你需要用python实现Softmax回归方法,用于MNIST手写数字数据集分类任务。你需要完成前向计算loss和参数更新。
你需要首先实现Softmax函数和交叉熵损失函数的计算。
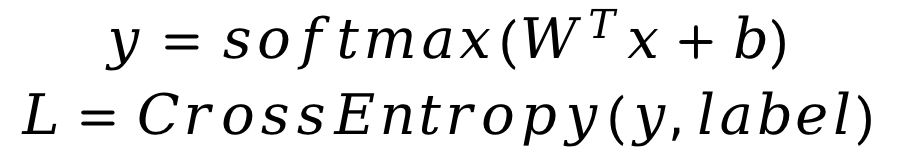
在更新参数的过程中,你需要实现参数梯度的计算,并按照随机梯度下降法来更新参数。
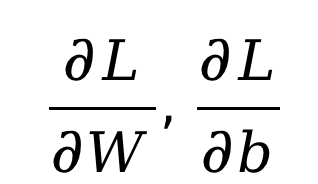
具体计算方法可自行推导,或参照第三章课件。
MNIST数据集
MNIST手写数字数据集是机器学习领域中广泛使用的图像分类数据集。它包含60,000个训练样本和10,000个测试样本。这些数字已进行尺寸规格化,并在固定尺寸的图像中居中。每个样本都是一个784×1的矩阵,是从原始的28×28灰度图像转换而来的。MNIST中的数字范围是0到9。下面显示了一些示例。 注意:在训练期间,切勿以任何形式使用有关测试样本的信息。

任务要求
- 代码清单
a) data/ 文件夹:存放MNIST数据集。你需要下载数据,解压后存放于该文件夹下。下载链接见文末,解压后的数据为 *ubyte 形式;
b) solver.py 这个文件中实现了训练和测试的流程。建议从这个文件开始阅读代码;
c) dataloader.py 实现了数据加载器,可用于准备数据以进行训练和测试;
d) visualize.py 实现了plot_loss_and_acc函数,该函数可用于绘制损失和准确率曲线;
e) optimizer.py 你需要实现带momentum的SGD优化器,可用于执行参数更新;
f) loss.py 你需要实现softmax_cross_entropy_loss,包含loss的计算和梯度计算;
g) runner.ipynb 完成所有代码后的执行文件,执行训练和测试过程。
- 要求
我们提供了完整的代码框架,你只需要完成optimizer.py,loss.py 中的 #TODO部分。你需要提交整个代码文件和带有结果的 runner.ipynb ( 不要提交数据集 ) 并且附一个pdf格式报告,内容包括:
a) 记录训练和测试的准确率。画出训练损失和准确率曲线;
b) 比较使用和不使用momentum结果的不同,可以从训练时间,收敛性和准确率等方面讨论差异;
c) 调整其他超参数,如学习率,Batchsize等,观察这些超参数如何影响分类性能。写下观察结果并将这些新结果记录在报告中。
3.其他
- 注意代码的执行效率,尽量不要使用for循环;
- 不要在pdf报告中粘贴很多代码(只能包含关键代码),对添加的代码作出解释;
- 不要使用任何深度学习框架,如TensorFlow,Pytorch等;
- 禁止抄袭。
4.参考
- 数据集下载:http://yann.lecun.com/exdb/mnist/
核心代码
optimizer.py
def step(self):"""One updating step, update weights"""layer = self.modelif layer.trainable:############################################################################# TODO: Put your code here# Calculate diff_W and diff_b using layer.grad_W and layer.grad_b.# You need to add momentum to this.# Weight update with momentumself.diff_W = self.momentum * self.diff_W - self.learning_rate * layer.grad_Wself.diff_b = self.momentum * self.diff_b - self.learning_rate * layer.grad_b# # Weight update without momentumlayer.W += self.diff_Wlayer.b += self.diff_b############################################################################
loss.py
class SoftmaxCrossEntropyLoss(object):def __init__(self, num_input, num_output, trainable=True):"""Apply a linear transformation to the incoming data: y = Wx + bArgs:num_input: size of each input samplenum_output: size of each output sampletrainable: whether if this layer is trainable"""self.num_input = num_inputself.num_output = num_outputself.trainable = trainableself.XavierInit()def onehot_labels(self , labels):'''one-hot lable'''lable_one = np.zeros((labels.shape[0],10))for i in range(len(labels)):lable_one[i,labels[i]] = 1 return lable_one def forward(self, Input, labels):"""Inputs: (minibatch)- Input: (batch_size, 784)- labels: the ground truth label, shape (batch_size, )"""############################################################################# TODO: Put your code here# Apply linear transformation (WX+b) to Input, and then# calculate the average accuracy and loss over the minibatch# Return the loss and acc, which will be used in solver.py# Hint: Maybe you need to save some arrays for gradient computing.self.z = np.exp(np.dot(Input, self.W) + self.b) # z = wx + b self.z = (self.z + EPS) / ((np.sum(self.z, axis = 1).reshape(-1,1)) + EPS) # z = exp(Zi) / sum(exp(Zi))self.lables = self.onehot_labels(labels)# onehot_labelsloss = np.mean(-np.log(np.sum( self.z * self.lables, axis=1))) # loss = - y lg(z)logit = np.nanargmax(self.z, axis=1) # outputacc = sum([ int(i == j) for (i ,j) in zip(logit, labels)]) / len(labels) # compute accself.Input , self.label = Input , labels #save arraysreturn loss, acc############################################################################def gradient_computing(self):############################################################################# TODO: Put your code here# Calculate the gradient of W and b.grad = self.z - self.lablesself.grad_b = np.nanmean( grad ,axis = 0) self.grad_W = np.dot(self.Input.T,grad) / self.Input.shape[0]############################################################################