题单介绍：

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。

题单介绍：

题目：560. 和为 K 的子数组 - 力扣（Leetcode）

题目的接口：

解题思路：

代码：

过过过过啦！！！！

题目：543. 二叉树的直径 - 力扣（Leetcode）

题目的接口：

解题思路：

代码：

过过过过啦！！！！

写在最后：

题目：560. 和为 K 的子数组 - 力扣（Leetcode）

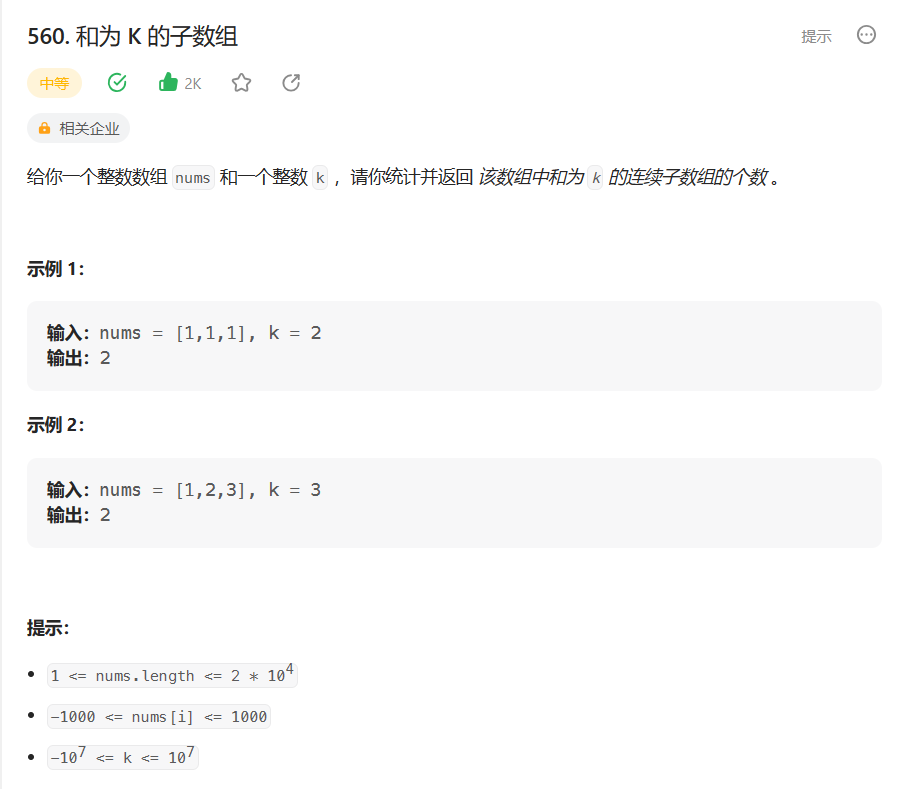
题目的接口：

class Solution {
public:int subarraySum(vector<int>& nums, int k) {}
};

解题思路：

遇到这种题目，

先不管三七二十一马上暴力试一下能不能过完样例：

class Solution {
public:int subarraySum(vector<int>& nums, int k) {int cnt = 0;for(int i = 0; i < nums.size(); i++) {int sum = 0;for(int j = i; j < nums.size(); j++) {sum += nums[j];if(sum == k) cnt++;}}return cnt;}
};

好的失败了：

那就没办法用暴力求解了，

老老实实想该怎么优化这个算法，

这道题可以用前缀和 + 哈希来做，

具体思路如下：

等等，官方题解有详细的视频解说，

解说是个小姐姐，声音非常好听，强烈建议自己去听一下，

那我这里就不讲解思路了，传送门：560. 和为 K 的子数组 - 力扣（Leetcode）

代码如下：

代码：

class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> mp;mp[0] = 1;int cnt = 0, preSum = 0;for(const auto& e : nums) {preSum += e;if(mp.find(preSum - k) != mp.end()) {cnt += mp[preSum - k];}mp[preSum]++;}return cnt;}
};

过过过过啦！！！！

题目：543. 二叉树的直径 - 力扣（Leetcode）

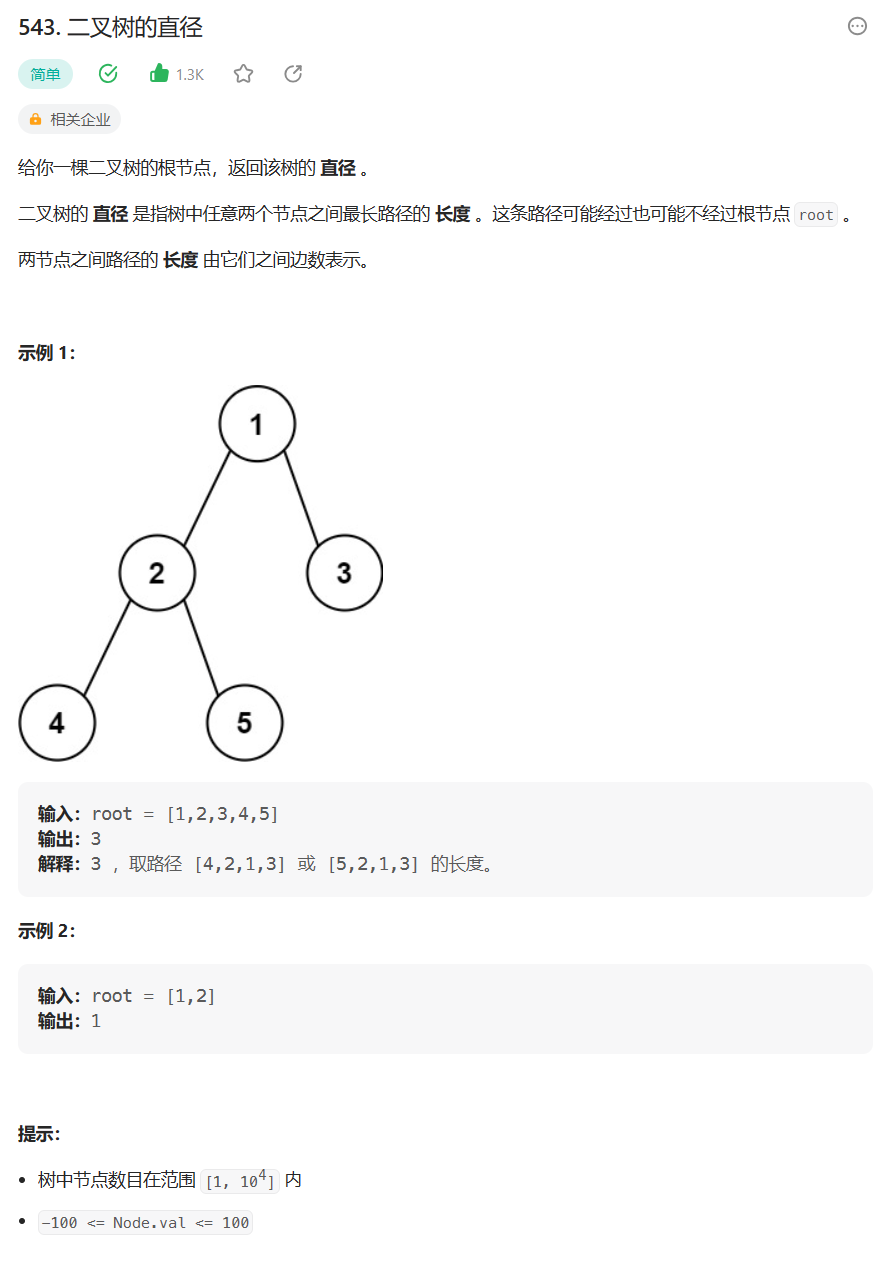
题目的接口：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int ans = 0;int diameterOfBinaryTree(TreeNode* root) {}
};

解题思路：

久违的简单题，

这道题的思路并不难，根据题意，

找最长的直径，不难想到，

找一棵树的最长直径其实就是找这个树中，

每一棵子树的左子树的最大深度 + 右子树的最大深度（当然你说最大高度也行）

然后他们之中的最大值其实就是树的最大直径，

来看代码：

代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int ans = 0;int diameterOfBinaryTree(TreeNode* root) {depth(root);return ans;}
private:int depth(TreeNode* root) {if(root == nullptr) return 0;int left = depth(root->left);  //左子树的最大深度int right = depth(root->right);//右子树的最大深度ans = max(ans, left + right);  //找出直径最长的子树return max(left, right) + 1;   //这个是查找最大深度}
};