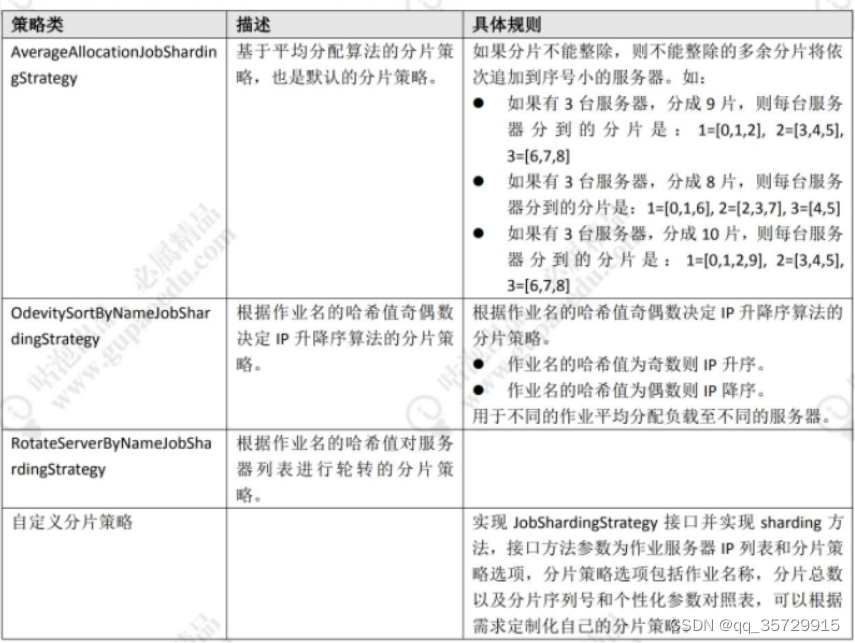
题目描述

 

大h喜欢玩游戏。有一天，他下载了一款名为“Bloxorz”的电脑游戏，令他兴奋不已。这是一个关于在地面上将盒子滚动到特定位置的游戏。确切地说，由许多1*1的地砖组成的平面矩形区域。盒子是一个底面为1*1，高为2的立方体，可以平放并占据两个相邻的地砖或竖放并占据一个地砖。人们可以通过在地面上挑选盒子的四个方向中的一个来移动盒子并且将盒子向该方向滚动90度，这被计为一次移动。有三种地砖，普通地砖，易碎地砖和空地砖。普通可以支撑盒子的全部重量，易碎地砖只能支撑盒子重量的一半，所以盒子不能竖放在它上面。空地砖不能承重，也就是盒子的任意部分不能在它上面。游戏的目标是以最少的移动次数将盒子竖放在上唯一的目标地砖上。

盒子竖放一个地砖上：

盒子水平放置在两个相邻的地砖上：

盒子垂直放置在两个相邻的地砖上：

大h在通过游戏的几个阶段后，他发现这游戏比他预期的要简单得多。所以他打算写一个游戏脚本来计算最少移动次数。

 

输入

 

 

输入包含多组数据。每组数据以两个整数R和C（3≤R，C≤500）开始，它代表地面面的行数和列数。接下来R行，每行C个字符，目标地砖为'O'，盒子的初始位置为'X'，'.'表示普通地砖，'#'表示空地砖，“E”表示易碎地砖。数据以两个零结尾。

输入保证：

地面上只有一个'O'。

在地面上有一个'X'或相邻的两个'X'。

第一行（列）和最后一行（列）一定是“＃”（空地砖）

 

 

输出

 

 

每组数据一行，若可以完成游戏，则输出最小移动次数，否则输出"Impossible"（不带引号）。

 

 

样例输入

<span style="color:#333333"><span style="color:#333333">7 7
#######
#..X###
#..##O#
#....E#
#....E#
#.....#
#######
0 0</span></span>

样例输出 

<span style="color:#333333"><span style="color:#333333">10</span></span>

题解：设计Dist[i][j][k]表示从起点出发到(i,j)，k表示不同的方法。

如0，1，2，3表示横放的四个方向，4表示竖放。

然后跑一遍最短路即可 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
struct Node
{int x,y,p,dis;//bool operator < (const Node &T) const {return dis>T.dis;}
};
queue<Node>que;
int n,m,sx,sy,sx1,sy1,Dist[505][505][6],zx,zy;char ch[505][505];
const int dx[4]={0,-1,0,1},dy[4]={1,0,-1,0};
bool pd(int x,int y)
{if(x>0&&x<=n&&y>0&&y<=m)return true;return false;
}
int main()
{while(1){scanf("%d%d",&n,&m);if(!n&&!m)break;for(int i=1;i<=n;++i)scanf(" %s",ch[i]+1);sx=sy=0;for(int i=1;i<=n;++i)for(int j=1;j<=m;++j){if(ch[i][j]=='X'){if(!sx)sx=i,sy=j;else sx1=i,sy1=j;}if(ch[i][j]=='O')zx=i,zy=j;}for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)for(int k=0;k<5;++k)Dist[i][j][k]=1e9;if(!sx1){Dist[sx][sy][4]=0;que.push((Node){sx,sy,4,0});}else {int t;for(t=0;t<4;t++){if(sx+dx[t]==sx1&&sy+dy[t]==sy1)break;}Dist[sx][sy][t]=0;que.push((Node){sx,sy,t,0});}while(!que.empty()){Node t=que.front();que.pop();//cout<<"aaa "<<t.x<<' '<<t.y<<' '<<t.p<<' '<<t.dis<<endl;if(Dist[t.x][t.y][t.p]!=t.dis)continue;if(t.p==4){for(int i=0;i<4;++i){int nx1=t.x+dx[i],ny1=t.y+dy[i],nx2=nx1+dx[i],ny2=ny1+dy[i];if(!pd(nx1,ny1)||!pd(nx2,ny2))continue;if(ch[nx1][ny1]=='#'||ch[nx2][ny2]=='#')continue;if(Dist[nx1][ny1][i]>Dist[t.x][t.y][4]+1){Dist[nx1][ny1][i]=Dist[t.x][t.y][4]+1;//Dist[nx2][ny2][(i+2)%4]=Dist[t.x][t.y][4]+1;que.push((Node){nx1,ny1,i,Dist[nx1][ny1][i]});}}continue;}int nx1=t.x+dx[(t.p+2)%4],ny1=t.y+dy[(t.p+2)%4],nx2,ny2,sum;if(pd(nx1,ny1)){if(Dist[nx1][ny1][4]>t.dis+1&&ch[nx1][ny1]!='#'&&ch[nx1][ny1]!='E'){Dist[nx1][ny1][4]=t.dis+1;que.push((Node){nx1,ny1,4,t.dis+1});}}nx1=t.x+2*dx[t.p],ny1=t.y+2*dy[t.p];if(pd(nx1,ny1)){if(Dist[nx1][ny1][4]>t.dis+1&&ch[nx1][ny1]!='#'&&ch[nx1][ny1]!='E'){Dist[nx1][ny1][4]=t.dis+1;que.push((Node){nx1,ny1,4,t.dis+1});}}if(!t.p||t.p==2){nx1=nx2=t.x+1;ny1=t.y;ny2=ny1+dy[t.p];if(pd(nx1,ny1)&&pd(nx2,ny2)){   if(Dist[nx1][ny1][t.p]>t.dis+1&&ch[nx1][ny1]!='#'&&ch[nx2][ny2]!='#'){Dist[nx1][ny1][t.p]=t.dis+1;Dist[nx2][ny2][(t.p+2)%4]=t.dis+1;que.push((Node){nx1,ny1,t.p,t.dis+1});}}nx1=nx2=t.x-1;ny1=t.y;ny2=ny1+dy[t.p];if(pd(nx1,ny1)&&pd(nx2,ny2)){if(Dist[nx1][ny1][t.p]>t.dis+1&&ch[nx1][ny1]!='#'&&ch[nx2][ny2]!='#'){Dist[nx1][ny1][t.p]=t.dis+1;Dist[nx2][ny2][(t.p+2)%4]=t.dis+1;que.push((Node){nx1,ny1,t.p,t.dis+1});}}}if(t.p==1||t.p==3){ny1=ny2=t.y+1;nx1=t.x;nx2=t.x+dx[t.p];if(pd(nx1,ny1)&&pd(nx2,ny2)){if(Dist[nx1][ny1][t.p]>t.dis+1&&ch[nx1][ny1]!='#'&&ch[nx2][ny2]!='#'){Dist[nx1][ny1][t.p]=t.dis+1;Dist[nx2][ny2][(t.p+2)%4]=t.dis+1;que.push((Node){nx1,ny1,t.p,t.dis+1});}}ny1=ny2=t.y-1;nx1=t.x;nx2=t.x+dx[t.p];if(pd(nx1,ny1)&&pd(nx2,ny2)){if(Dist[nx1][ny1][t.p]>t.dis+1&&ch[nx1][ny1]!='#'&&ch[nx2][ny2]!='#'){Dist[nx1][ny1][t.p]=t.dis+1;Dist[nx2][ny2][(t.p+2)%4]=t.dis+1;que.push((Node){nx1,ny1,t.p,t.dis+1});}}}}if(Dist[zx][zy][4]==1e9)puts("Impossible");else printf("%d\n",Dist[zx][zy][4]);}
}