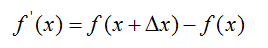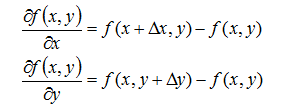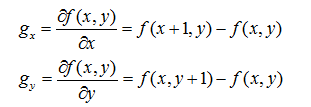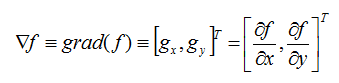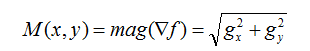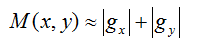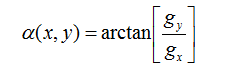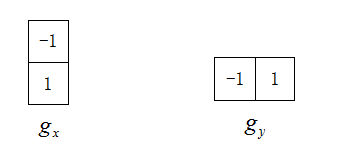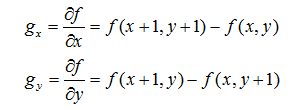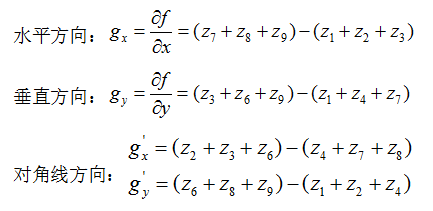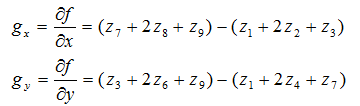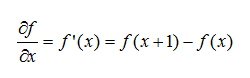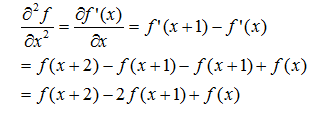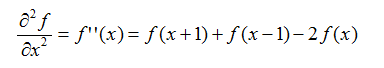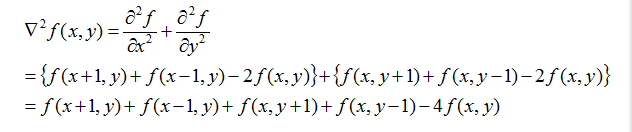算子推导过程
1、知识引入:
在一维连续数集上有函数f(x),我们可以通过求导获得该函数在任一点的斜率,根据导数的定义有:
在二维连续数集上有函数f(x,y),我们也可以通过求导获得该函数在x和y分量的偏导数,根据定义有:
2、梯度和Roberts算子:
对于图像来说,是一个二维的离散型数集,通过推广二维连续型求函数偏导的方法,来求得图像的偏导数,即在(x,y)处的最大变化率,也就是这里的梯度:
梯度是一个矢量,则(x,y)处的梯度表示为:
其大小为:
因为平方和平方根需要大量的计算开销,所以使用绝对值来近似梯度幅值:
方向与α(x,y)正交:
其对应的模板为:
上面是图像的垂直和水平梯度,但我们有时候也需要对角线方向的梯度,定义如下:
对应模板为:
上述模板就是Roberts交叉梯度算子。
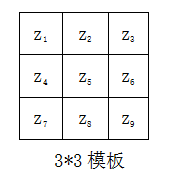
2*2大小的模板在概念上很简单,但是他们对于用关于中心点对称的模板来计算边缘方向不是很有用,其最小模板大小为3*3。3*3模板考虑了中心点对段数据的性质,并携带有关于边缘方向的更多信息。
3、Prewitt和Sobel算子:
在3*3模板中:
如下定义水平、垂直和两对角线方向的梯度:
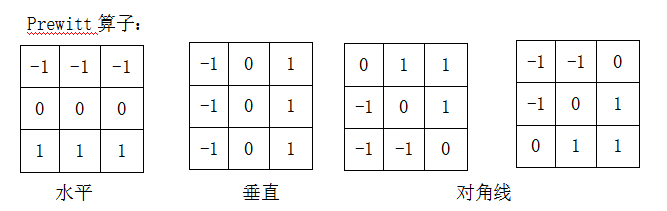
该定义下的算子称之为Prewitt算子:
Sobel算子是在Prewitt算子的基础上改进的,在中心系数上使用一个权值2,相比较Prewitt算子,Sobel模板能够较好的抑制(平滑)噪声。
计算公式为:
Sobel算子: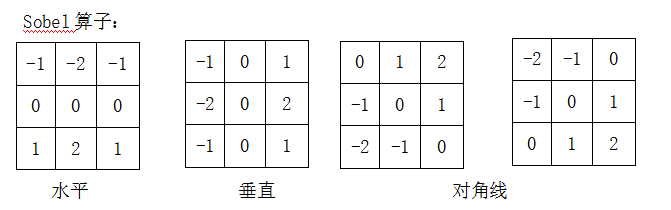
上述所有算子都是通过求一阶导数来计算梯度的,用于线的检测,在图像处理中,通常用于边缘检测。在图像处理过程中,除了检测线,有时候也需要检测特殊点,这就需要用二阶导数进行检测。
4、Lapacian算子:
一阶导数:
二阶导数:
我们感兴趣的是关于点x的二阶导数,故将上式中的变量减1后,得到:
在图像处理中通过拉普拉斯模板求二阶导数,其定义如下:
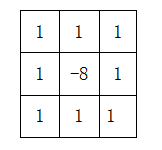
对应模板为:
模板中心位置的数字是-8而不是-4,是因为要使这些系数之和为0,当遇到恒定湖对区域时,模板响应应将0。
在用lapacian算子图像进行卷积运算时,当响应的绝对值超过指定阈值时,那么该点就是被检测出来的孤立点,具体输出如下: