目录

快速排序

 并查集

亲戚

 新二叉树

 美国血统

求先序排列

 遍历问题

 二叉树深度

搭配购买

​

朋友

   修复公路

刻录光盘

---

快速排序

题目描述

利用快速排序算法将读入的 NN 个数从小到大排序后输出。

快速排序是信息学竞赛的必备算法之一。对于快速排序不是很了解的同学可以自行上网查询相关资料，掌握后独立完成。（C++ 选手请不要试图使用 STL，虽然你可以使用 sort 一遍过，但是你并没有掌握快速排序算法的精髓。）

输入格式

第 11 行为一个正整数 NN，第 22 行包含 NN 个空格隔开的正整数 a_iai​，为你需要进行排序的数，数据保证了 A_iAi​ 不超过 10^9109。

输出格式

将给定的 NN 个数从小到大输出，数之间空格隔开，行末换行且无空格。

输入输出样例

输入 #1复制

5
4 2 4 5 1

输出 #1复制

1 2 4 4 5

说明/提示

对于 20\%20% 的数据，有 N\leq 10^3N≤103；

对于 100\%100% 的数据，有 N\leq 10^5N≤105。

思路分析：

  这道题刚开始用的是常规的快排，但是超时了两个点，然后一直在缩短代码，但一直都是超时。后来换了一种思路，常规思路是把每一次要排序的第一个数当成关键数，可是由于会有特殊情况例如数组本来就有序，或者是有大量的重复数字。为了提高程序的效率，这里把每次要排序的最中间的数字当成关键数字，然后其他的和常规快排是一样的，唯一不同的就是在递归的时候，常规快排是直接分两部分开始递归，可这里由于是从中间开始的，所以会存在有一边已经排好序的情况，因此需要判断两端搜索的变量是否到底。

代码实现： 

#include<stdio.h>
int n,a[1000001];
void swap(int *a,int *b)//利用指针交换两个数
{int k;k=*a;*a=*b;*b=k;
}
void quick(int begin,int end)
{int mid=a[(begin+end)/2];//取每次要排序的最中间那个数int left=begin,right=end;do{while(a[left]<mid) left++;while(a[right]>mid) right--;if(left<=right){swap(&a[left],&a[right]);left++;right--;}}while(left<=right);if(begin<right) quick(begin,right);//如果右探测器还没到达最左端，即部分还需要继续排序if(left<end) quick(left,end);//同上反之
}
int main()
{    scanf("%d",&n);for(int i=0;i<n;i++) scanf("%d",&a[i]);quick(0,n-1);for(int i=0;i<n;i++) printf("%d ",a[i]);return 0;
}

 并查集

题目描述

如题，现在有一个并查集，你需要完成合并和查询操作。

输入格式

第一行包含两个整数 N,MN,M ,表示共有 NN 个元素和 MM 个操作。

接下来 MM 行，每行包含三个整数 Z_i,X_i,Y_iZi​,Xi​,Yi​ 。

当 Z_i=1Zi​=1 时，将 X_iXi​ 与 Y_iYi​ 所在的集合合并。

当 Z_i=2Zi​=2 时，输出 X_iXi​ 与 Y_iYi​ 是否在同一集合内，是的输出 Y ；否则输出 N 。

输出格式

对于每一个 Z_i=2Zi​=2 的操作，都有一行输出，每行包含一个大写字母，为 Y 或者 N 。

输入输出样例

输入 #1复制

4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4

输出 #1复制

N
Y
N
Y

说明/提示

对于 30\%30% 的数据，N \le 10N≤10，M \le 20M≤20。

对于 70\%70% 的数据，N \le 100N≤100，M \le 10^3M≤103。

对于 100\%100% 的数据，1\le N \le 10^41≤N≤104，1\le M \le 2\times 10^51≤M≤2×105，1 \le X_i, Y_i \le N1≤Xi​,Yi​≤N，Z_i \in \{ 1, 2 \}Zi​∈{1,2}。

思路分析：

  这道题主要就是并查集的查询和合并操作。然后我们把每个节点的上一个节点成为父亲，每个节点的最顶端节点称为祖先。刚开始把每个节点的父亲都设为本身（因为还没有开始合并，都是独立的节点）。然后如果输入的z如果是1的话，就合并x和y两个节点，这里采用的方法是，将x节点的祖先指向y节点的祖先，这样他们就算合并了。那么找寻祖先的方法就是判断如果当前节点的父亲就是其本身，那么证明其就是祖先，如果不是的话，就把当前节点的的祖先等于上一个节点的祖先，这样的同一集合中的节点的祖先就都是相同的。

  当输入的z等于2时，就判断x的祖先和y的祖先是否相同，如果相同就代表两个结点属于同一集合，输出"Y"，反之。

代码实现： 

#include<stdio.h>
int n;
long long m;
int f[10010];//存放每个节点的足祖先
int z,x,y;
int find(int a)//寻找当前节点的祖先
{if(f[a]==a)//如果当前节点的祖先等于本身，那么证明该节点就是当前集合的祖先return a; else{f[a]=find(f[a]);//当前节点的祖先等于父亲节点的祖先return f[a];}
}
void combine(int x,int y)//合并两个节点
{   int f1,f2;f1=find(x);f2=find(y);f[f1]=f2;//x节点的祖先等于Y节点的祖先
}
int main()
{scanf("%d %d",&n,&m);for(int i=1;i<=n;i++)f[i]=i;for(long long i=1;i<=m;i++){scanf("%d %d %d",&z,&x,&y);if(z==1){  combine(x,y); }else if(z==2){if(find(x)==find(y))//判断两个节点的祖先是否相同printf("Y\n");else printf("N\n");}}return 0;
}

亲戚

题目背景

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

题目描述

规定：xx 和 yy 是亲戚，yy 和 zz 是亲戚，那么 xx 和 zz 也是亲戚。如果 xx，yy 是亲戚，那么 xx 的亲戚都是 yy 的亲戚，yy 的亲戚也都是 xx 的亲戚。

输入格式

第一行：三个整数 n,m,pn,m,p，（n,m,p \le 5000n,m,p≤5000），分别表示有 nn 个人，mm 个亲戚关系，询问 pp 对亲戚关系。

以下 mm 行：每行两个数 M_iMi​，M_jMj​，1 \le M_i,~M_j\le N1≤Mi​, Mj​≤N，表示 M_iMi​ 和 M_jMj​ 具有亲戚关系。

接下来 pp 行：每行两个数 P_i,P_jPi​,Pj​，询问 P_iPi​ 和 P_jPj​ 是否具有亲戚关系。

输出格式

pp 行，每行一个 Yes 或 No。表示第 ii 个询问的答案为“具有”或“不具有”亲戚关系。

输入输出样例

输入 #1复制

6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6

输出 #1复制

Yes
Yes
No

 思路分析：

  这道题和并查集模板那道题的思路是一模一样的，只不过这里输入亲戚关系和输入判断是否有亲戚关系是分开输入的。前面输入亲戚关系的时候直接调用合并函数就行。后面判断亲戚关系的时候就是判断两个人是否有共同的亲戚，也就是判断祖先是否相同。

代码实现： 

#include<stdio.h>
int n,m,p;
int f[5010];
int find(int x)
{if(f[x]==x)return x;else{f[x]=find(f[x]);return f[x];}
}
void combine(int x,int y)
{f[find(x)]=find(y);
}
int main()
{    int mi,mj,pi,pj;scanf("%lld %lld %lld",&n,&m,&p);for(int i=1;i<=n;i++)f[i]=i;for(int i=1;i<=m;i++){scanf("%d %d",&mi,&mj);combine(mi,mj);}for(int i=1;i<=p;i++){scanf("%d %d",&pi,&pj);if(find(pi)==find(pj))printf("Yes\n");else printf("No\n");}return 0;
}

 新二叉树

题目描述

输入一串二叉树，输出其前序遍历。

输入格式

第一行为二叉树的节点数 nn。(1 \leq n \leq 261≤n≤26)

后面 nn 行，每一个字母为节点，后两个字母分别为其左右儿子。

空节点用 * 表示

输出格式

二叉树的前序遍历。

输入输出样例

输入 #1复制

6
abc
bdi
cj*
d**
i**
j**

输出 #1复制

abdicj

思路分析： 

  这道题比较简单，这里我没用才用建树的方法，直接用的递归。因为每次输入的第一个字母就是根节点，因此每次进入函数的时候输出根节点，然后递归其子节点即可。这里需要找到根节点在输入的时候所对应的那一串，只要不是'#'，就开始继续向下遍历。由于前序遍历的顺序是：根左右，因此每次在函数中输出根之后，就是先遍历左儿子再遍历右儿子。

代码实现：

#include<bits/stdc++.h>
using namespace std;
struct node//定义一个结构体包括当前节点以及其左右两个儿子
{char fa;char left;char right;
}a[100];
int n;
void bian(char c)
{cout<<c;//输出节点for(int i=0;i<n;i++){if(a[i].fa==c){if(a[i].left!='*')bian(a[i].left);//遍历左儿子if(a[i].right!='*')bian(a[i].right);//遍历右儿子}}
}
int main()
{cin>>n;    for(int i=0;i<n;i++){cin>>a[i].fa>>a[i].left>>a[i].right;}bian(a[0].fa);//从最开始的根节点开始遍历return 0;
}

 美国血统

题目描述

农夫约翰非常认真地对待他的奶牛们的血统。然而他不是一个真正优秀的记帐员。他把他的奶牛 们的家谱作成二叉树，并且把二叉树以更线性的“树的中序遍历”和“树的前序遍历”的符号加以记录而 不是用图形的方法。

你的任务是在被给予奶牛家谱的“树中序遍历”和“树前序遍历”的符号后，创建奶牛家谱的“树的 后序遍历”的符号。每一头奶牛的姓名被译为一个唯一的字母。（你可能已经知道你可以在知道树的两 种遍历以后可以经常地重建这棵树。）显然，这里的树不会有多于 26 个的顶点。 这是在样例输入和 样例输出中的树的图形表达方式：

　　　　　　　　 C/  \/　　\B　　  G/ \　　/A   D  H/ \E   F

树的中序遍历是按照左子树，根，右子树的顺序访问节点。

树的前序遍历是按照根，左子树，右子树的顺序访问节点。

树的后序遍历是按照左子树，右子树，根的顺序访问节点。

输入格式

第一行： 树的中序遍历

第二行： 同样的树的前序遍历

输出格式

单独的一行表示该树的后序遍历。

输入输出样例

输入 #1复制

ABEDFCHG
CBADEFGH 

输出 #1复制

AEFDBHGC

 思路分析：

  首先根据观察我们可以发现前序遍历的第一个节点就是总的根节点，然后在中序遍历中找到总根节点的位置，由于中序遍历是左根右，因此中序遍历中最左边就是左子树的左边界，总根节点的左边就是左子树的右边界，总根节点的右边就是右子树的左边界，中序遍历的最右边就是右子树的右边界。依次类推，分为左右子树递归，求各自的次根节点。然后由于后序遍历是左右根，因此在每次递归完当前左右子树之后就输出根节点的值。

代码实现：

#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
char mid[100];
char fir[100];
int i,j;
void dian(int fl,int fr,int ml,int mr)//前序遍历的左右边界，中序遍历的左右边界
{int gen,llen,rlen;for(i=0;strlen(mid);i++)if(mid[i]==fir[fl])//找到根节点在中序遍历中的位置break;gen=i;llen=gen-ml;//记录左子树中节点的数量rlen=mr-gen;//记录右子树中节点的数量if(llen>0){dian(fl+1,fl+llen,ml,ml+llen-1);//递归前序和中序的左子树}if(rlen>0){dian(fr-rlen+1,fr,gen+1,gen+rlen);//递归前序和中序的右子树}cout<<fir[fl];//输出根节点
}
int main()
{cin>>mid>>fir;dian(0,strlen(fir)-1,0,strlen(mid)-1);return 0;
}

求先序排列

题目描述

给出一棵二叉树的中序与后序排列。求出它的先序排列。（约定树结点用不同的大写字母表示，长度\le 8≤8）。

输入格式

22行，均为大写字母组成的字符串，表示一棵二叉树的中序与后序排列。

输出格式

11行，表示一棵二叉树的先序。

输入输出样例

输入 #1复制

BADC
BDCA

输出 #1复制

ABCD

 思路分析：

  通过观察我们可以得出，后序排列的最后一个节点就是根节点，然后我们在中序排列中找到根节点的位置，然后左边就是左子树，右边就是右子树。求出左右子树的大小，如果存在的话就开始递归，左子树的左边界就是中序遍历的第一个节点，左子树的有边界就是根节点的左边一个节点。右子树的左边界就是根节点的右边一个节点，右边界就是中序遍历的最后一个节点，以此类推，递归两个子树。由于前序遍历是根左右，因此在递归两个子树之前输出根节点的值。

代码实现： 

#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
char mid[100];//中序遍历
char las[100];//后序遍历
int i,j;
void bian(int ml,int mr,int ll,int lr)
{int gen;for(i=0;strlen(mid);i++)if(mid[i]==las[lr])//找到根节点在中序遍历中的位置break;gen=i;int ln,rn;ln=gen-ml;rn=mr-gen;cout<<las[lr];if(ln>0){bian(ml,ml+ln-1,ll,ll+ln-1);//递归左子树}if(rn>0){bian(gen+1,gen+rn,lr-rn,lr-1);//递归右子树}
}
int main()
{cin>>mid;cin>>las;bian(0,strlen(mid)-1,0,strlen(las)-1);return 0;
}

 遍历问题

 

题目描述

我们都很熟悉二叉树的前序、中序、后序遍历，在数据结构中常提出这样的问题：已知一棵二叉树的前序和中序遍历，求它的后序遍历，相应的，已知一棵二叉树的后序遍历和中序遍历序列你也能求出它的前序遍历。然而给定一棵二叉树的前序和后序遍历，你却不能确定其中序遍历序列，考虑如下图中的几棵二叉树：

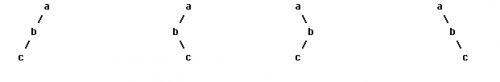
所有这些二叉树都有着相同的前序遍历和后序遍历，但中序遍历却不相同。

输入格式

输A数据共两行，第一行表示该二叉树的前序遍历结果s1，第二行表示该二叉树的后序遍历结果s2。

输出格式

输出可能的中序遍历序列的总数，结果不超过长整型数。

输入输出样例

输入 #1复制

abc                           
cba

输出 #1复制

4

思路分析

   这里考察的是，当二叉树中每个根只有一个结点时，有多少种情况。通过观察我们可以发现，当两个结点在前序遍历中的顺序和在后序遍历中的逆序相同时，就代表只有一个结点，不确定子结点属于左子树还是右子树，因此中序遍历中这一段就存在两种情况，然后总的情况是2的指数增长的。

代码实现： 

#include<iostream>
#include<algorithm>
using namespace std;
char fir[1000];
char las[1000];
int sum=1;
int main()
{     cin>>fir>>las;for(int i=0;fir[i];i++)for(int j=1;las[j];j++)if(fir[i]==las[j]&&fir[i+1]==las[j-1])//判断两个结点在前序编列中的顺序和后序遍历中的逆序是否相同sum*=2;//2的倍数增加cout<<sum;return 0;
}

 二叉树深度

题目描述

给出每个节点的两个儿子节点，建立一棵二叉树（根节点为 11），如果是叶子节点，则输入0 0。建好树后希望知道这棵二叉树的深度。二叉树的深度是指从根节点到叶子结点时，最多经过了几层。

最多有 10^6106 个结点。

输入格式

无

输出格式

无

输入输出样例

输入 #1复制

7
2 7
3 6
4 5
0 0
0 0
0 0
0 0

输出 #1复制

4

 思路分析：

  输入时的每一行（第一行除外）代表的就是该结点的两个子树。因此这里是一个简单的递归操作，递归的参数是当前结点序号和当前的层数（从第一层开始），然后递归左右两个子树。递归结束的条件就是遇到0的时候，就代表没有子结点了。每次调用递归函数，不断更新层数的最大值，最后直接输出最大值即可。

 代码实现：

#include<bits/stdc++.h>
using namespace std;
struct node//定义一个结构题存储当前结点的左右两个子树
{int left;int right;
}a[1000010];
int n;//结点个数
int maxd;
void depth(int n,int dep)
{if(n==0)return;maxd=maxd>dep?maxd:dep;//更新层数的最大值depth(a[n].left,dep+1);//递归左子树depth(a[n].right,dep+1);//递归右子树
}
int main()
{cin>>n;for(int i=1;i<=n;i++)cin>>a[i].left>>a[i].right;depth(1,1);cout<<maxd;return 0;
}

搭配购买

题目描述

明天就是母亲节了，电脑组的小朋友们在忙碌的课业之余挖空心思想着该送什么礼物来表达自己的心意呢？听说在某个网站上有卖云朵的，小朋友们决定一同前往去看看这种神奇的商品，这个店里有 nn 朵云，云朵已经被老板编号为 1,2,3,...,n1,2,3,...,n，并且每朵云都有一个价值，但是商店的老板是个很奇怪的人，他会告诉你一些云朵要搭配起来买才卖，也就是说买一朵云则与这朵云有搭配的云都要买，电脑组的你觉得这礼物实在是太新奇了，但是你的钱是有限的，所以你肯定是想用现有的钱买到尽量多价值的云。

输入格式

第一行输入三个整数，n,m,wn,m,w，表示有 nn 朵云，mm 个搭配和你现有的钱的数目。

第二行至 n+1n+1 行，每行有两个整数， c_i,d_ici​,di​，表示第 ii 朵云的价钱和价值。

第 n+2n+2 至 n+1+mn+1+m 行 ，每行有两个整数 u_i,v_iui​,vi​。表示买第 u_iui​ 朵云就必须买第 v_ivi​ 朵云,同理，如果买第 v_ivi​ 朵就必须买第 u_iui​ 朵。

输出格式

一行，表示可以获得的最大价值。

输入输出样例

输入 #1复制

5 3 10
3 10
3 10
3 10
5 100
10 1
1 3
3 2
4 2

输出 #1复制

1

思路分析： 

    这里相当于是把具有捆绑关系的云看成一个整体，然后利用背包问题的做法，求出可以获得的最大价值。在输入云朵的捆绑关系时，定义两个变量存储两个云朵当前的祖先，然后判断如果祖先相同的话，就直接跳到输入下一组捆绑关系，如果不相同，就将其中一个云朵的祖先指向另一个云朵的祖先，这样他们的祖先就相同了，并且还需要将他们的价钱和价值累加起来，注意：这里累加的应该是需要合并云朵的前祖先，因为现祖先已经改变了。

  然后就是利用背包问题的思想，行是每一个云朵，列是当前的钱。然后依次枚举云朵，如果当前云朵的父亲是本身代表它是这个整体的祖先，然后就开始循环从最大价钱到该祖先的价钱，取放与不放的较大值。最后直接输出用最多价钱时的价值就是最大价值。

 代码实现：

#include<stdio.h>
int n,m,wi,w[5000000],v[5000000],f[5000000],dp[500000];
int max(int a,int b)
{if(a>b)return a;return b;
}
int find(int n)//返回当前云朵的祖先
{if(f[n]==n)return n;f[n]=find(f[n]);return f[n];
}
void combine(int a,int b)//合并两个云朵
{f[find(b)]=find(a);
}
int main()
{scanf("%d %d %d",&n,&m,&wi);for(int i=1;i<=n;i++)scanf("%d %d",w+i,v+i),f[i]=i;for(int i=1;i<=m;i++){   int a,b,A,B;scanf("%d %d",&a,&b);A=find(a);B=find(b);if(find(a)==find(b))continue;combine(a,b);v[A]+=v[B];//累加操作都是祖先之间的，因为祖先代表整体的价钱和价值w[A]+=w[B];}for(int i=1;i<=n;i++)if(f[i]==i)//找到整体的祖先{for(int j=wi;j>=w[i];j--)dp[j]=max(dp[j],dp[j-w[i]]+v[i]);//取较大值}printf("%d",dp[wi]);return 0;
}

朋友

题目背景

小明在 A 公司工作，小红在 B 公司工作。

题目描述

这两个公司的员工有一个特点：一个公司的员工都是同性。

A 公司有 NN 名员工，其中有 PP 对朋友关系。B 公司有 MM 名员工，其中有 QQ 对朋友关系。朋友的朋友一定还是朋友。

每对朋友关系用两个整数 (X_i,Y_i)(Xi​,Yi​) 组成，表示朋友的编号分别为 X_i,Y_iXi​,Yi​。男人的编号是正数，女人的编号是负数。小明的编号是 11，小红的编号是 -1−1。

大家都知道，小明和小红是朋友，那么，请你写一个程序求出两公司之间，通过小明和小红认识的人最多一共能配成多少对情侣（包括他们自己）。

输入格式

输入的第一行，包含 44 个空格隔开的正整数 N,M,P,QN,M,P,Q。

之后 PP 行，每行两个正整数 X_i,Y_iXi​,Yi​。

之后 QQ 行，每行两个负整数 X_i,Y_iXi​,Yi​。

输出格式

输出一行一个正整数，表示通过小明和小红认识的人最多一共能配成多少对情侣（包括他们自己）。

输入输出样例

输入 #1复制

4 3 4 2
1 1
1 2
2 3
1 3
-1 -2
-3 -3

输出 #1复制

2

 

 思路分析：

  这道题就是把小明和小红的认识的人分为两个集体，然后取较少的那个（因为是两两配对）。依次枚举输入的关系，然后进行合并，注意在判断有多少认识的人时，不一定所有人的祖先都得是小明或者小红，因为他们也可能只是集体中的一个结点，因此只需判断同属一个祖先即可。

代码实现： 

#include<iostream>
#include<algorithm>
using namespace std;
int n,m,p,q;
int a,b;
int f1[1000000];
int f2[1000000];
int sum1=0,sum2=0;
int find(int *f,int n)
{ if(f[n]==n)return n;f[n]=find(f,f[n]);return f[n];
}
void combine(int *f,int a,int b)
{f[find(f,b)]=find(f,a);
}
int main()
{cin>>n>>m>>p>>q;int length=max(m,n);for(int i=1;i<=length;i++)//对数组进行初始化{f1[i]=i;f2[i]=i;}for(int i=1;i<=p;i++){cin>>a>>b;if(find(f1,a)==find(f1,b))continue;combine(f1,a,b);}for(int i=1;i<=q;i++){cin>>a>>b;a*=-1;b*=-1;if(find(f2,a)==find(f2,b))continue;combine(f2,a,b);}for(int i=1;i<=n;i++)if(find(f1,i)==find(f1,1))//如果当前结点与小明的祖先相同，代表他们是互相认识的sum1++;for(int i=1;i<=m;i++)if(find(f2,i)==find(f2,1))//如果当前结点与小红的祖先相同，代表他们是互相认识的sum2++;cout<<min(sum1,sum2);//取两人朋友数量较小者return 0;
}

   修复公路

题目背景

AA地区在地震过后，连接所有村庄的公路都造成了损坏而无法通车。政府派人修复这些公路。

题目描述

给出A地区的村庄数NN，和公路数MM，公路是双向的。并告诉你每条公路的连着哪两个村庄，并告诉你什么时候能修完这条公路。问最早什么时候任意两个村庄能够通车，即最早什么时候任意两条村庄都存在至少一条修复完成的道路（可以由多条公路连成一条道路）

输入格式

第11行两个正整数N,MN,M

下面MM行，每行33个正整数x, y, tx,y,t，告诉你这条公路连着x,yx,y两个村庄，在时间t时能修复完成这条公路。

输出格式

如果全部公路修复完毕仍然存在两个村庄无法通车，则输出-1−1，否则输出最早什么时候任意两个村庄能够通车。

输入输出样例

输入 #1复制

4 4
1 2 6
1 3 4
1 4 5
4 2 3

输出 #1复制

5

 思路分析：

   这道题的思路就是，先将输入的公路连着的两个村庄和时间点存储到结构体数组中，再用快速排序按照时间的先后进行排序（用其他排序会超时）。然后再按照时间的顺序，依次合并两个村庄，并设置一个变量等于原本的村庄数，每合并两个村庄，该变量就-1，直到等于1的时候就代表任意两个村庄都通车了，然后输出当前的时间即可。

 代码实现：

#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
long long n,m;
struct node
{long long x;long long y;long long t;
}a[1000010],k;
int f[10000010];
void quick(int begin,int end)//快速排序函数
{int mid=a[(begin+end)/2].t;//取每次要排序的最中间那个数int left=begin,right=end;do{while(a[left].t<mid) left++;while(a[right].t>mid) right--;if(left<=right){k=a[left];a[left]=a[right];a[right]=k;left++;right--;}}while(left<=right);if(begin<right) quick(begin,right);//如果右探测器还没到达最左端，即部分还需要继续排序if(left<end) quick(left,end);//同上反之
}
long long find(long long n)
{if(f[n]==n)return n;f[n]=find(f[n]);return f[n];
}
void combine(long long a,long long b)
{f[find(b)]=find(a);
}
int main()
{  scanf("%d %d",&n,&m);for(long long i=1;i<=n;i++)f[i]=i;for(long long i=1;i<=m;i++){cin>>a[i].x>>a[i].y>>a[i].t;//将输入的两两村庄的连通情况存储到结构体数组中}quick(1,m);for(long long i=1;i<=m;i++){if(find(a[i].x)==find(a[i].y))//如果两个村庄的祖先相同，证明他们就是连通的continue;combine(a[i].x,a[i].y);//连通两个村庄n--;if(n==1){cout<<a[i].t;return 0;}}cout<<-1;return 0;}

刻录光盘

题目描述

在JSOI2005夏令营快要结束的时候，很多营员提出来要把整个夏令营期间的资料刻录成一张光盘给大家，以便大家回去后继续学习。组委会觉得这个主意不错！可是组委会一时没有足够的空光盘，没法保证每个人都能拿到刻录上资料的光盘，又来不及去买了，怎么办呢？！

组委会把这个难题交给了LHC，LHC分析了一下所有营员的地域关系，发现有些营员是一个城市的，其实他们只需要一张就可以了，因为一个人拿到光盘后，其他人可以带着U盘之类的东西去拷贝啊！

可是，LHC调查后发现，由于种种原因，有些营员并不是那么的合作，他们愿意某一些人到他那儿拷贝资料，当然也可能不愿意让另外一些人到他那儿拷贝资料，这与我们JSOI宣扬的团队合作精神格格不入！！！

现在假设总共有N个营员（2<=N<=200），每个营员的编号为1~N。LHC给每个人发了一张调查表，让每个营员填上自己愿意让哪些人到他那儿拷贝资料。当然，如果A愿意把资料拷贝给B，而B又愿意把资料拷贝给C，则一旦A获得了资料，则B，C都会获得资料。

现在，请你编写一个程序，根据回收上来的调查表，帮助LHC计算出组委会至少要刻录多少张光盘，才能保证所有营员回去后都能得到夏令营资料？

输入格式

先是一个数N，接下来的N行，分别表示各个营员愿意把自己获得的资料拷贝给其他哪些营员。即输入数据的第i+1行表示第i个营员愿意把资料拷贝给那些营员的编号，以一个0结束。如果一个营员不愿意拷贝资料给任何人，则相应的行只有1个0，一行中的若干数之间用一个空格隔开。

输出格式

一个正整数，表示最少要刻录的光盘数。

输入输出样例

输入 #1复制

5
2 3 4 0
4 5 0
0
0
1 0

输出 #1复制

1

思路分析： 

  这道题一开始用并查集做的，只对了28，想了很久才发现不能用并查集做。因为并查集的两个结点之间是双向的，但这道题的意思是单向的。例如在并查集中，A愿意分给B，那么他们就可以互相分享，但在这道题中B就不能分给A。因此这里需要先记录下来输入的所有传递关系，再利用一个三层循环，枚举每个点当中间点，找出传递关系，这样就可以枚举出所有的传递关系。最后只需判断有多少个结点的父亲为本身，就代表有多少个集体，等于需要刻录多少光盘。

代码实现：

#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
int n;
int sum;
int f[10000];
int map[1000][1000];//记录下传递关系
int find(int n)
{if(f[n]==n)return n;f[n]=find(f[n]);return f[n];
}
void combine(int x, int y) {f[y] = find(x); 
} 
int main()
{cin>>n;for(int i=1;i<=n;i++)f[i]=i;for(int i=1;i<=n;i++){    int k;cin>>k;while(k!=0){map[i][k]=1;//标记已有的传递关系cin>>k;}}               for(int k=1;k<=n;++k)//枚举每个点作为中间点，标记新增的传递关系for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)if(map[i][j]||(map[i][k]&&map[k][j]))map[i][j]=1;     for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)if(map[i][j])//合并结点combine(i,j);for(int i=1;i<=n;++i)if(f[i]==i)//判断有多少个团体sum++;                     cout<<sum;return 0;
}