【MR】现代机器人学-UR5机械臂正向动力学仿真-2(零外力、零关节力矩、初始J2=-1rad)...

news/2024/11/25 15:49:06/

Python计算仿真生成路径点csv文件，coppeliasim加载路径点进行可视化演示。

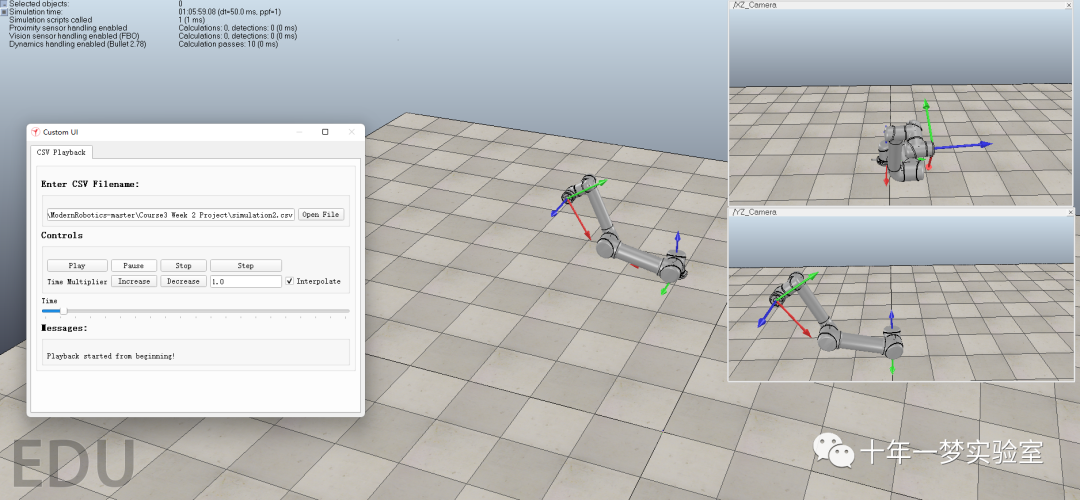仿真截图

Coppeliasim加载仿真结果视频演示

Python程序：基于MR算法库的正向动力学仿真

import numpy as np
import modern_robotics as mr
from pprint import pprintnp.set_printoptions(formatter={'float': lambda x: "{0:0.3f}".format(x)})M01 = [[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0.089159], [0, 0, 0, 1]]
M12 = [[0, 0, 1, 0.28], [0, 1, 0, 0.13585], [-1, 0, 0, 0], [0, 0, 0, 1]]
M23 = [[1, 0, 0, 0], [0, 1, 0, -0.1197], [0, 0, 1, 0.395], [0, 0, 0, 1]]
M34 = [[0, 0, 1, 0], [0, 1, 0, 0], [-1, 0, 0, 0.14225], [0, 0, 0, 1]]
M45 = [[1, 0, 0, 0], [0, 1, 0, 0.093], [0, 0, 1, 0], [0, 0, 0, 1]]
M56 = [[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0.09465], [0, 0, 0, 1]]
M67 = [[1, 0, 0, 0], [0, 0, 1, 0.0823], [0, -1, 0, 0], [0, 0, 0, 1]]
G1 = np.diag([0.010267495893, 0.010267495893,  0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689067591, 0.22689067591, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.049443313556, 0.049443313556, 0.004095, 2.275, 2.275, 2.275])
G4 = np.diag([0.111172755531, 0.111172755531, 0.21942, 1.219, 1.219, 1.219])
G5 = np.diag([0.111172755531, 0.111172755531, 0.21942, 1.219, 1.219, 1.219])
G6 = np.diag([0.0171364731454, 0.0171364731454, 0.033822, 0.1879, 0.1879, 0.1879])
Glist = [G1, G2, G3, G4, G5, G6]
Mlist = [M01, M12, M23, M34, M45, M56, M67] 
Slist = [[0,         0,         0,         0,        0,        0],[0,         1,         1,         1,        0,        1],[1,         0,         0,         0,       -1,        0],[0, -0.089159, -0.089159, -0.089159, -0.10915, 0.005491],[0,         0,         0,         0,  0.81725,        0],[0,         0,     0.425,   0.81725,        0,  0.81725]]
#关节初始配置  J2=-1 rad
thetalist = np.array([0.0, -1, 0.0, 0.0, 0.0, 0.0])
dthetalist = np.zeros((6,))
taulist = np.zeros((6,))
g = np.array([0.0, 0.0, -9.81])
Ftip = np.zeros((6,))
dt = 0.005thetamat = thetalist.copy()for i in range(1000):ddthetalist = mr.ForwardDynamics(thetalist, dthetalist, taulist, g, Ftip, Mlist, Glist, Slist)[thetalist, dthetalist] = mr.EulerStep(thetalist, dthetalist, ddthetalist, dt)thetamat = np.vstack((thetamat, thetalist))np.savetxt("simulation2.csv", thetamat, delimiter=",")

输出结果：