【dfs解决分组问题-两道例题——供佬学会！】（A元素是放在已经存在的组别中，还是再创建一个更好？--小孩子才做选择，dfs直接两种情况都试试）

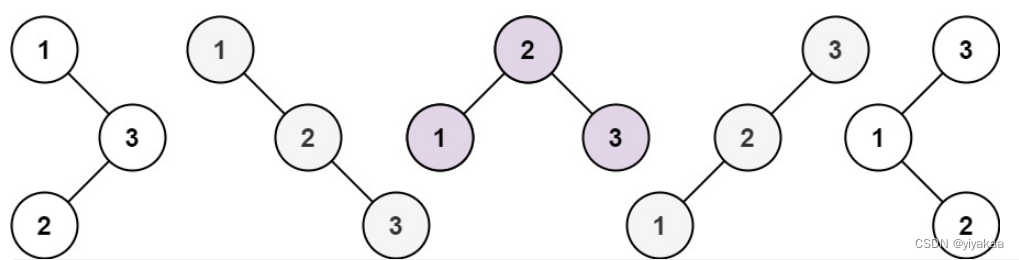
问题关键就是：
一个点，可能
新开一个组
比
放到已经存在的组
更划算
因为后面的数据，我们遍历之前的点时，并不知道
所以我们应该针对每个点，都应该做出一个选择就是
新开一个元组或者放到之前的元组中，都尝试一次(截取重点内容，继续往下看)

我们发现这道题目有两个可以剪枝的部分,
一个是如果当前的答案已经大于了我们已知的最小答案,不用说直接return返回即可.
第二个剪枝则是,我们可以将小猫的体重从大到小排序,这样我们的搜索树就会缩短许多,至于为什么,因为我们的剩余空间就变小了,然后可选择的猫也就少了
(截取重点内容，继续往下看)

欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
　
文章字体风格：
红色文字表示：重难点★✔
蓝色文字表示：思路以及想法★✔
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！

dfs解决分组问题

- 分成互质组
- - - 错误想法：从头遍历，如果不匹配，则开新组
    - 正确想法：小孩子才做选择，dfs直接两种情况都试试
- 小猫爬山
- - - 减枝思想！！！

分成互质组

在这里插入图片描述
首先什么是互质？

互质就是彼此的最大公约数是 1

求a，b的最大公约数

int gcd(int a,int b)
{while(b){int c = a % b;a = b;b = c;}return a;
}

错误想法：从头遍历，如果不匹配，则开新组

本题，我的想法是：
从头遍历，如果不匹配，则开新组

用样例说就是

6
14 20 33 117 143 175选择20看之前已经开辟的 组别如果已经存在的 组别中的元素
和当前的不符合，那么换另一个组别再次尝试
如果都不合适，那么直接创建新组

错误代码
#include<iostream>
#include<vector>using namespace std;const int N = 11;int n;
int a[N];
vector<int> g[N];int gcd(int a,int b)
{while(b){int c = a % b;a = b;b = c;}return a;
}
int g_size;
void dfs(int u)
{if(u>n)return;for(int i = 1; i <= g_size; i++){int flag = 1;for(int j = 0; j < g[i].size(); j++){if(gcd(a[u],g[i][j])!=1){flag = 0;}}if(flag==1){// cout << a[u] << ' ';g[i].push_back(a[u]);dfs(u+1);return;}}g_size+=1;g[g_size].push_back(a[u]);dfs(u+1);return;
}int main()
{cin >> n;for(int i = 1; i <= n; i++)cin >> a[i];dfs(1);cout << g_size << endl;return 0;
}

正确想法：小孩子才做选择，dfs直接两种情况都试试

但是出现问题了

4
3 7 6 14这个样例 安上述思想 分组
3 7
6
14

分出3个组
但是

如果按着 正常分组
应该是 
3
7 6 14
这样更好

问题关键就是：
一个点，可能
新开一个组
比
放到已经存在的组
更划算
因为后面的数据，我们遍历之前的点时，并不知道
所以我们应该针对每个点，都应该做出一个选择就是
新开一个元组或者放到之前的元组中，都尝试一次

//正确代码
#include<iostream>
#include<vector>using namespace std;const int N = 11;int n;
int a[N];int gcd(int a,int b)
{while(b){int c = a % b;a = b;b = c;}return a;
}
int ans = 0x3f3f3f3f;
void dfs(int g_size,vector<int> g[N],int u)
{if(u>n){ans = min(g_size,ans);return;}for(int i = 1; i <= g_size; i++){int flag = 1;for(int j = 0; j < g[i].size(); j++){if(gcd(a[u],g[i][j])!=1){flag = 0;}}if(flag==1){// cout << a[u] << ' ';g[i].push_back(a[u]);dfs(g_size,g,u+1);g[i].pop_back();}}g[g_size+1].push_back(a[u]);dfs(g_size+1,g,u+1);g[g_size+1].pop_back();
}int main()
{cin >> n;for(int i = 1; i <= n; i++)cin >> a[i];vector<int> g[N];dfs(0,g,1);cout << ans << endl;return 0;
}

小猫爬山

在这里插入图片描述

减枝思想！！！

本题思路和上题一样，
但关键一点是，咱们可以借助本题，学会剪枝思想

当我们按某一种方案遍历过程时，发现走到一半发现这个方案，走到了一半已经比我之前走过的方案更费时费力，那么就直接不走这个方案了，减枝
或者走的过程中，按着从大到小或者从小到大走，这样说不定也会省时省力，也是减枝
或者就是我们知道了可实现的最坏情况
那么超过可实现的最坏情况，一定是不对的，直接不需要继续dfs了，也是剪枝

我们发现这道题目有两个可以剪枝的部分,
一个是如果当前的答案已经大于了我们已知的最小答案,不用说直接return返回即可.
第二个剪枝则是,我们可以将小猫的体重从大到小排序,这样我们的搜索树就会缩短许多,至于为什么,因为我们的剩余空间就变小了,然后可选择的猫也就少了

/** Project: 0x22_深度优先搜索* File Created:Sunday, January 24th 2021, 11:31:12 am* Author: Bug-Free* Problem:AcWing 165. 小猫爬山*/
#include <algorithm>
#include <iostream>using namespace std;const int N = 2e1;int cat[N], cab[N];
int n, w;
int ans;bool cmp(int a, int b) {return a > b;
}void dfs(int now, int cnt) {if (cnt >= ans) {return;}if (now == n + 1) {ans = min(ans, cnt);return;}//尝试分配到已经租用的缆车上for (int i = 1; i <= cnt; i++) {  //分配到已租用缆车if (cab[i] + cat[now] <= w) {cab[i] += cat[now];dfs(now + 1, cnt);cab[i] -= cat[now];  //还原}}// 新开一辆缆车cab[cnt + 1] = cat[now];dfs(now + 1, cnt + 1);cab[cnt + 1] = 0;
}int main() {cin >> n >> w;for (int i = 1; i <= n; i++) {cin >> cat[i];}sort(cat + 1, cat + 1 + n, cmp);ans = n;dfs(1, 0);cout << ans << endl;return 0;
}