1、从现实对象到数学模型
我们常见的模型
- 玩具、照片......~实物模型
- 水箱中的舰艇、风洞中的飞机......~物理模型
- 地图、电路图、分子结构图......~符号模型
模型是为了一定目的,对客观事物的一部分进行简缩、抽象、提炼出来的原型的替代物,集中反映了原型中人们需要的那一部分特征
数学模型和数学建模
数学模型:
对于一个现实对象,为了一个特定目的, 根据其内在规律,作出必要的简化假设, 运用适当的数学工具,得到的一个数学结构。
数学建模:
建立数学模型的全过程 (包括表述、求解、解释、检验等)
2、数学建模的重要意义
随着电子计算机的出现及飞速发展,数学以空前的广度和深度向一切领域渗透,数学建模作为用数学方法解决实际问题的第一步, 越来越受到人们的重视。在一般工程技术领域数学建模仍然大有用武之地,在高新技术领域数学建模几乎是必不可少的工具,数学进入一些新领域,为数学建模开辟了许多用武之地地
数学建模的具体应用
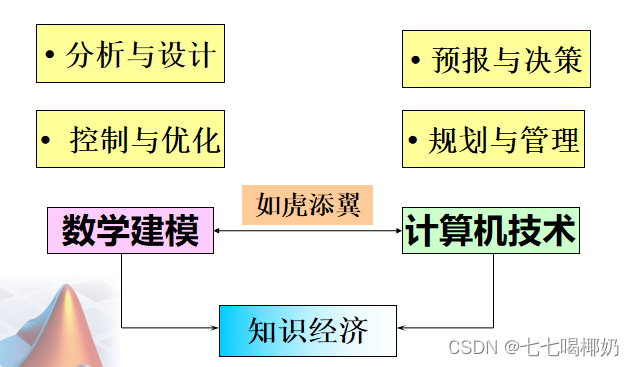
3、数学建模的方法和步骤
数学建模的基本方法:
- 机理分析:根据对客观事物特性的认识, 找出反映内部机理的数量规律
- 测试分析:将对象看作“黑箱”,通过对量测数据的 统计分析,找出与数据拟合最好的模型
而我们就是要结合二者,用机理分析建立模型结构, 用测试分析确定模型参数。
一般步骤:
数学建模的全过程:
4、 数学模型的特点
- 模型的逼真性和可行性
- 模型的渐进性
- 模型的强健性
- 模型的可转移性
- 模型的非预制性
- 模型的条理性
- 模型的技艺性
- 模型的局限性





