2023年5月17日
先回顾一下昨天的算法题,及答案
题目:寻找两个有序数组的中位数
给定两个大小分别为 m 和 n 的有序数组 nums1 和 nums2。请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例 1:
nums1 = [1, 3] nums2 = [2]
则中位数是 2.0
示例 2:
nums1 = [1, 2] nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
解答:
这道题可以使用二分查找的思想来解决,具体做法如下:
将两个有序数组合并为一个有序数组,这可以通过双指针法来实现,具体做法是维护两个指针 i 和 j,分别指向 nums1 和 nums2 的开头,每次比较两个指针所指的元素的大小,将较小的那个放入结果数组中,并将对应指针向后移动一位,直到遍历完两个数组为止。
如果数组的长度为奇数,则中位数是合并后数组的中间元素;如果数组的长度为偶数,则中位数是合并后数组中间两个元素的平均值。
具体实现代码如下:
function findMedianSortedArrays(nums1, nums2) {const len1 = nums1.length, len2 = nums2.length;const len = len1 + len2;const nums = new Array(len);let i = 0, j = 0, k = 0;while (i < len1 && j < len2) {if (nums1[i] <= nums2[j]) {nums[k++] = nums1[i++];} else {nums[k++] = nums2[j++];}}while (i < len1) {nums[k++] = nums1[i++];}while (j < len2) {nums[k++] = nums2[j++];}if (len % 2 === 0) {return (nums[len / 2 - 1] + nums[len / 2]) / 2;} else {return nums[Math.floor(len / 2)];}
}这个算法的时间复杂度为 O(m+n),并不满足题目要求,但是这里只是为了简化代码实现,如果要达到题目要求的时间复杂度 O(log(m+n)),可以使用类似二分查找的方法来优化代码实现。
2023年5月18日
题目:如何用一个数组来实现一个队列? 上面问题的答案会在第二天的公众号推文中公布,大家可以关注公众号,第一时间获得推送内容。
学习不打烊,充电加油只为遇到更好的自己,每天早上9点纯手工发布面试题(死磕自己,愉悦大家) 希望大家在这浮夸的程序员圈里保持冷静,每天坚持花20分钟来学习与思考,在千变万化,类库层出不穷的今天,不要等到找工作时才狂刷题,提倡每日学习。


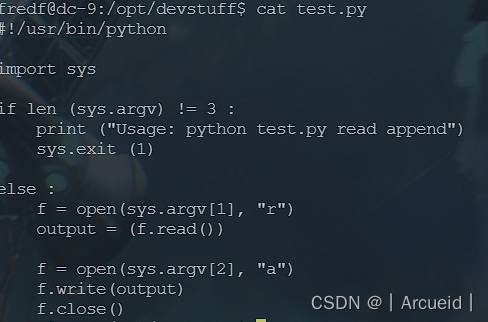

![C嘎嘎~~[类 下篇 之 日期类的实现]](https://img-blog.csdnimg.cn/8bf584c321634ba5ba6db3df84900e01.png)