【动态规划】子数组系列（上）

news/2024/11/24 6:56:17/

子数组问题

在这里插入图片描述

文章目录

  • 【动态规划】子数组系列（上）
    • 1. 最大子数组和
      • 1.1 题目解析
      • 1.2 算法原理
        • 1.2.1 状态表示
        • 1.2.2 状态转移方程
        • 1.2.3 初始化
        • 1.2.4 填表顺序
        • 1.2.5 返回值
      • 1.3 代码实现
    • 2. 环形子数组的最大和
      • 2.1 题目解析
      • 2.2 算法原理
        • 2.2.1 状态表示
        • 2.2.2 状态转移方程
        • 2.2.3 初始化
        • 2.2.4 填表顺序
        • 2.2.5 返回值
      • 3. 代码实现
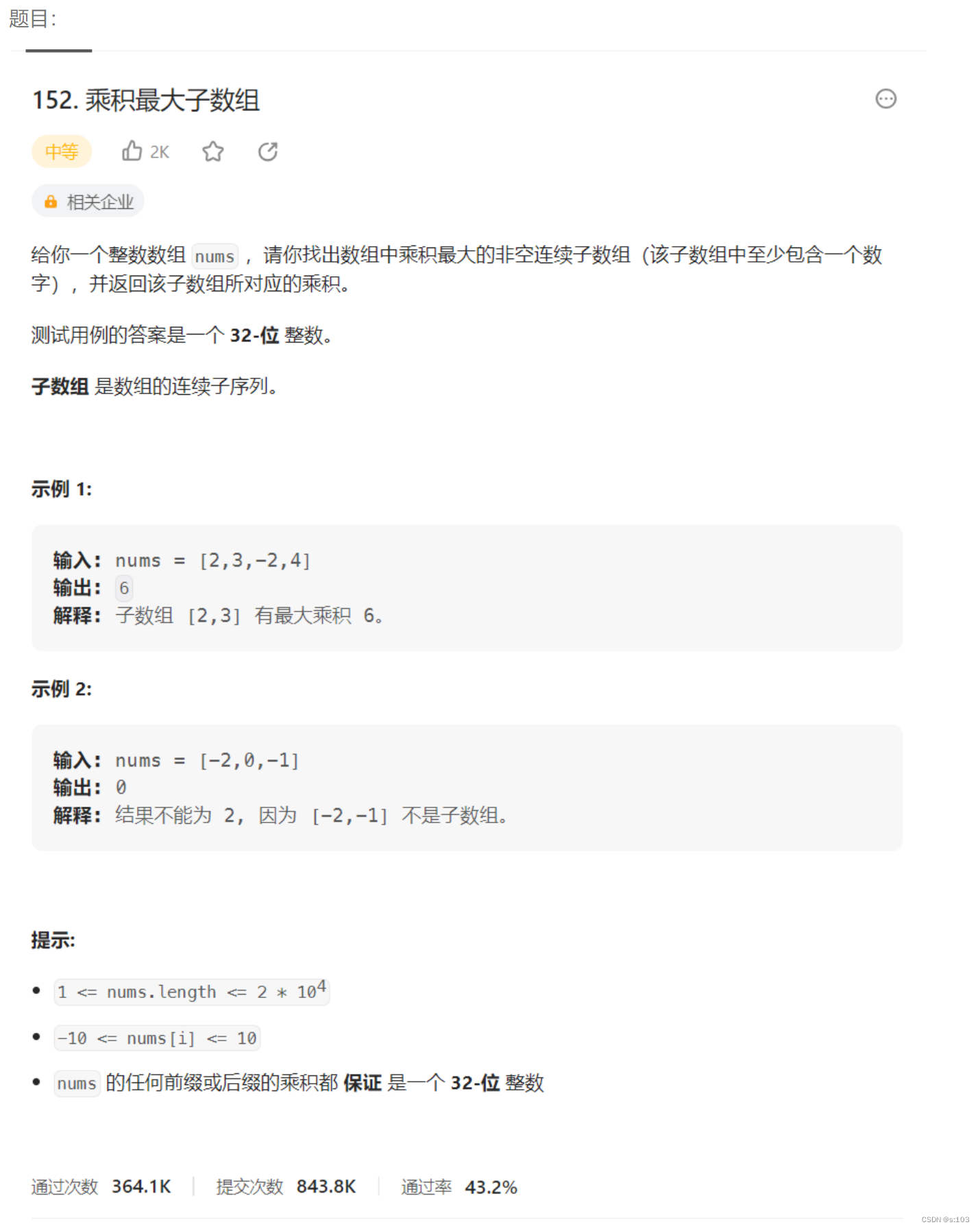
    • 3. 乘积最大子数组
      • 3.1 题目解析
      • 3.2 算法原理
        • 3.2.1 状态表示
        • 3.2.2 状态转移方程
        • 3.2.3 初始化
        • 3.2.4 填表顺序
        • 3.2.5 返回值
      • 3.3 编写代码
    • 4. 乘积为整数的最长子数组长度
      • 4.1 题目解析
      • 4.2 算法原理
        • 4.2.1 状态表示
        • 4.2.2 状态转移方程
        • 4.2.3 初始化
        • 4.2.4 填表顺序
        • 4.2.5 返回值
      • 4.3 代码实现

【动态规划】子数组系列（上）

1. 最大子数组和

传送门：力扣53最大子数组和

题目：

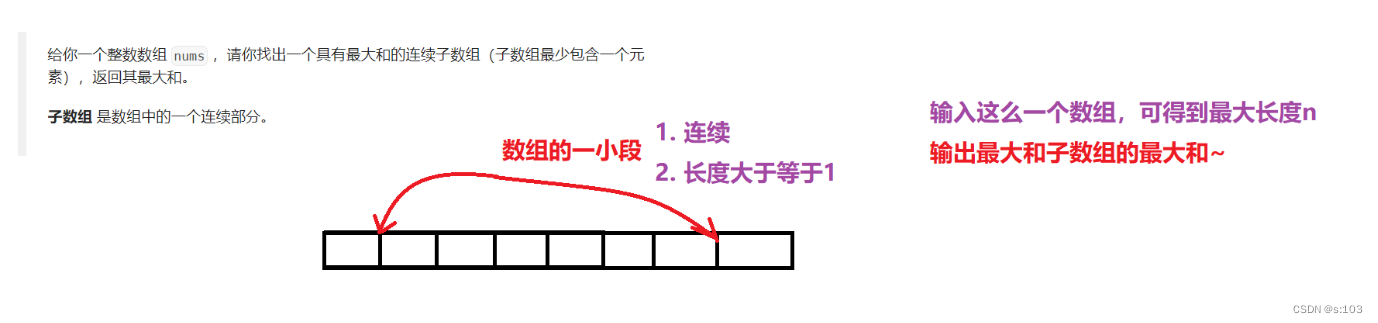
在这里插入图片描述

1.1 题目解析

在这里插入图片描述

示例：

在这里插入图片描述

1.2 算法原理

在没有学动态规划之前，我们的做法可能就是暴力得到所有子数组，求其中子数组和最大是多少~

  • 这里将以动态规划的方法去解决问题！

1.2.1 状态表示

这里的状态表示也是通过“经验 + 题目要求”

  • 题目要求：返回最大和，一维数组
    • 建立一维dp表，大小为n
    • 一维解决不了再上升二维
  • 经验：以什么为结尾 / 以什么为起点
    • 这里以…为结尾即可

得到状态表示：

  • dp[i]表示，以nums[i]为结尾的子数组中的最大和

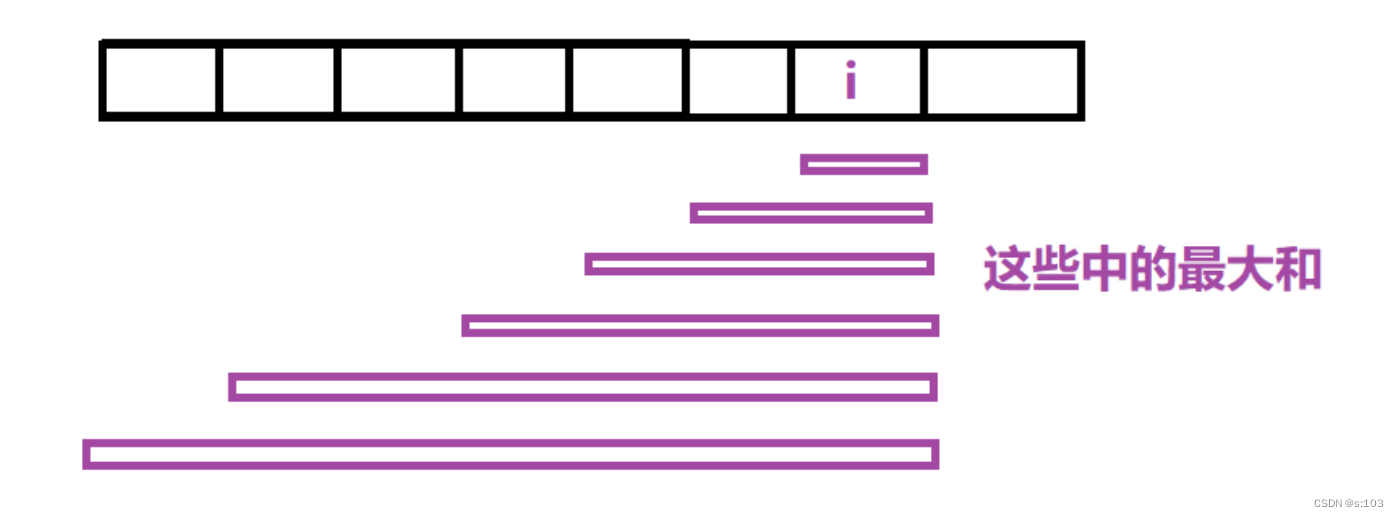
在这里插入图片描述

1.2.2 状态转移方程

得到状态转移方程的重点就是：

  1. 理清楚逻辑

    • 本题要分为两种情况：
    1. 一个元素的子数组
    2. 大于1个元素的子数组

  2. 理所当然地把dp表已填的数据当成绝对正确的值

以i为结尾，有两种情况：

  1. 子数组长度为1：nums[i]
  2. 子数组长度大于1：
    • 那么这个子数组至少有nums[i - 1]为结尾的子数组 + nums[i]
    • 所以就是max{nums[i - 1]为结尾的子数组和} + nums[i]
    • 即dp[i - 1] + nums[i]
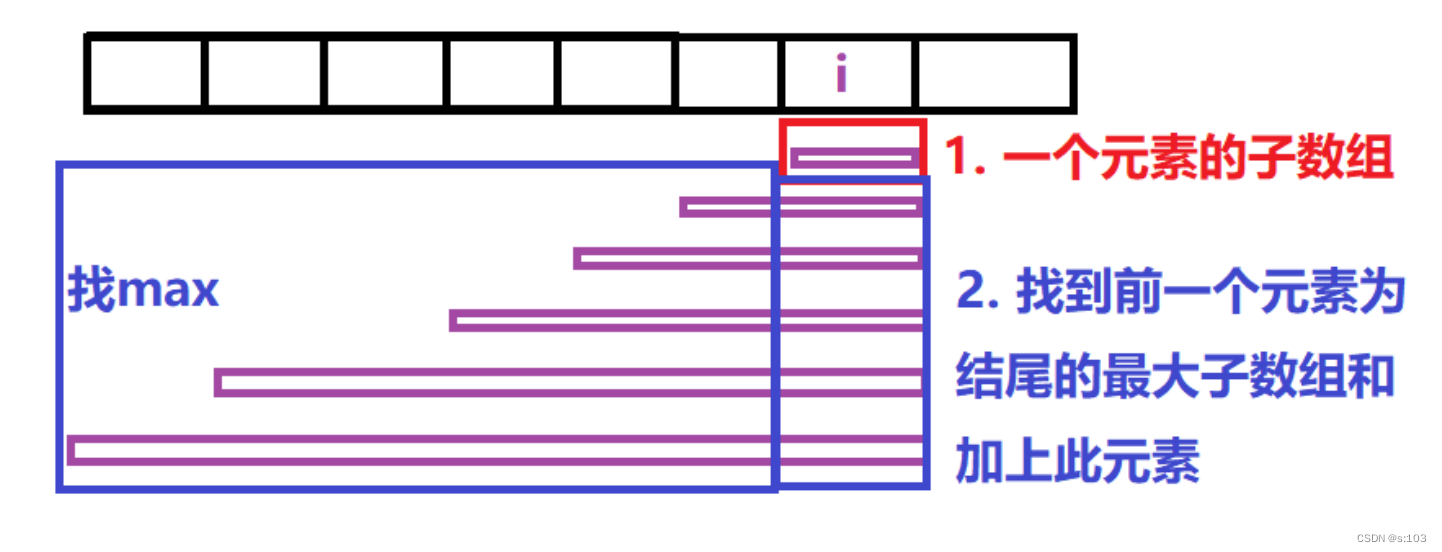
      在这里插入图片描述

得到状态转移方程：

dp[i] = nums[i] + max{0, dp[i - 1]};

1.2.3 初始化

对于第一个节点，需要规避一下越界问题~

  • 很明显，应该dp[0] = nums[0]

或者加虚拟节点 => 大小为（n+1），结合状态转移方程，dp[0] = 0不会影响dp表原有值

  • 注意：下标对应问题

在这里插入图片描述

1.2.4 填表顺序

从左往右填表，保证dp[i - 1]已填写

1.2.5 返回值

并不是返回最后一个节点的值哦，因为最大子数组和不一定以最后一个节点为结尾，而是求dp表的最大值

  • 不要算虚拟节点，因为这个数组全是负的的话，那么虚拟节点就为最大值了~

1.3 代码实现

class Solution {public int maxSubArray(int[] nums) {//1. 创建dp表//2. 初始化//3. 填表//4. 返回值int n = nums.length;int[] dp = new int[n + 1];int max = Integer.MIN_VALUE;for(int i = 1; i < n + 1; i++) {dp[i] = Math.max(0, dp[i - 1]) + nums[i - 1];max = Math.max(dp[i], max);}return max;}
}
  • 可以边填表边判断最大值
  • +nums[i - 1]哦，因为我们多加了个虚拟节点
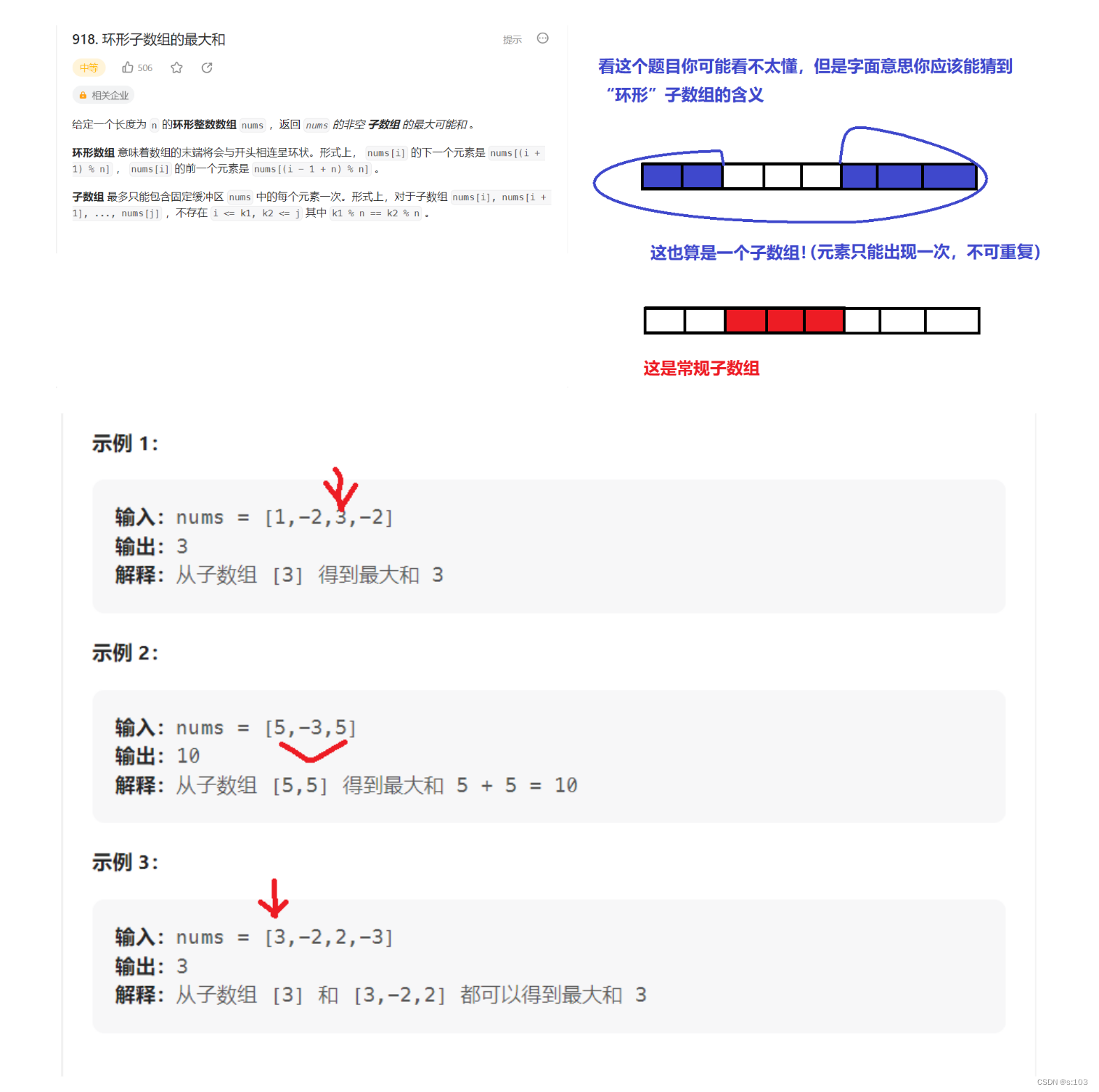
    在这里插入图片描述

2. 环形子数组的最大和

传送门：力扣918

题目：

在这里插入图片描述

2.1 题目解析

在这里插入图片描述

2.2 算法原理

2.2.1 状态表示

与前一道题一致：

在这里插入图片描述

但是我们可以注意到，如果这样的话，我们在填第一个数据的时候，dp[0]是填不出来的，并且dp[i - 1]可能包括了nums[i]这个点（由于环形）

所以在状态表示的时候就要进行逻辑的分析：

  • 我们可以分为两个情况：
  1. 常规子数组
  2. 环型子数组

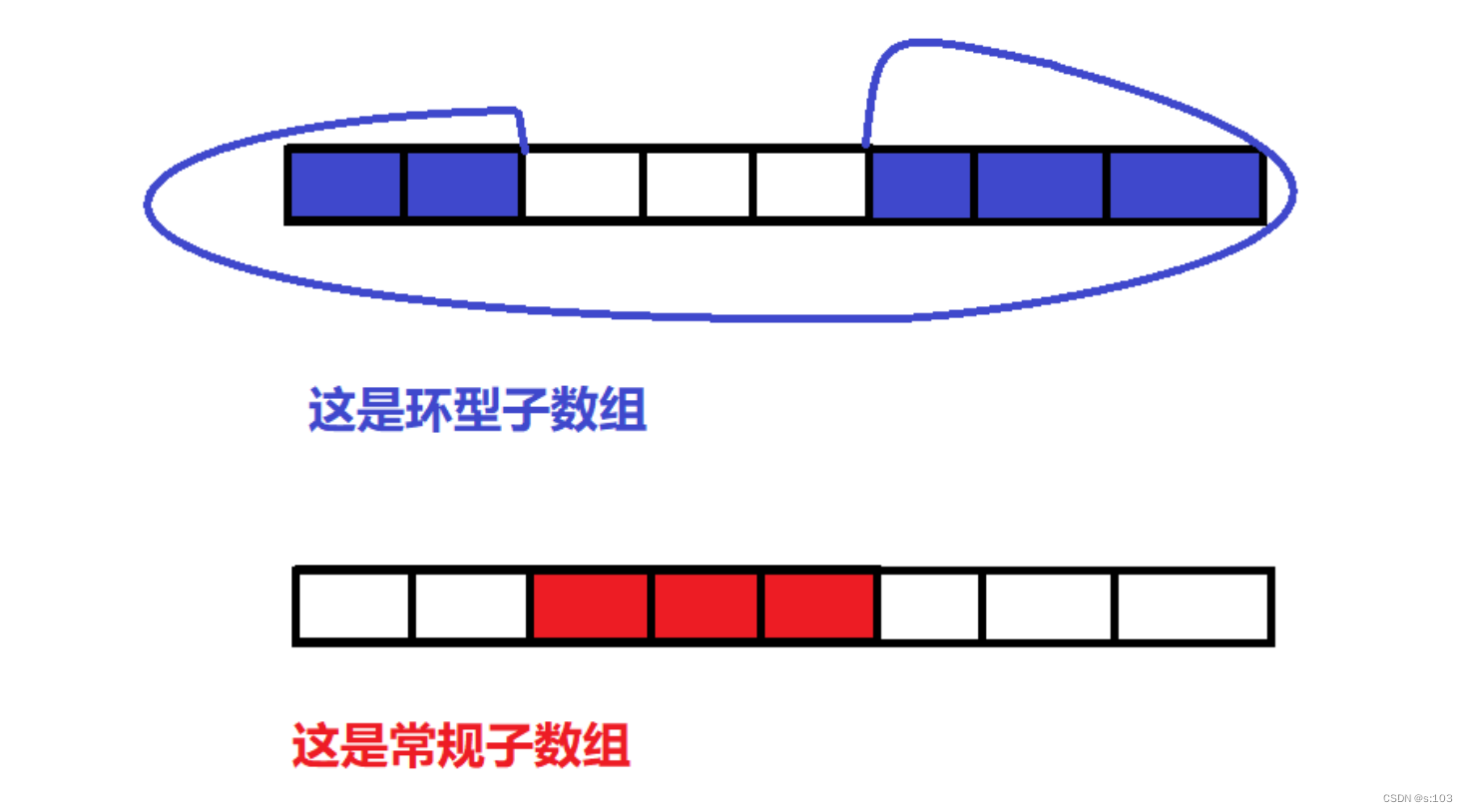
在这里插入图片描述

  • 而后者的求法是和常规的一样

前者则可以看成一下理解方式：

在这里插入图片描述

所以环形子数组的最大化就是紫色的最小化

  • 所以我们还需要知道“最小数组和”！
  • 这也演变成了多状态问题！

f[i]代表已i为结尾的子数组的最大和

g[i]代表已i为结尾的子数组的最小和

而这两个都不考虑“环”的存在！

2.2.2 状态转移方程

f，g表两者类似：

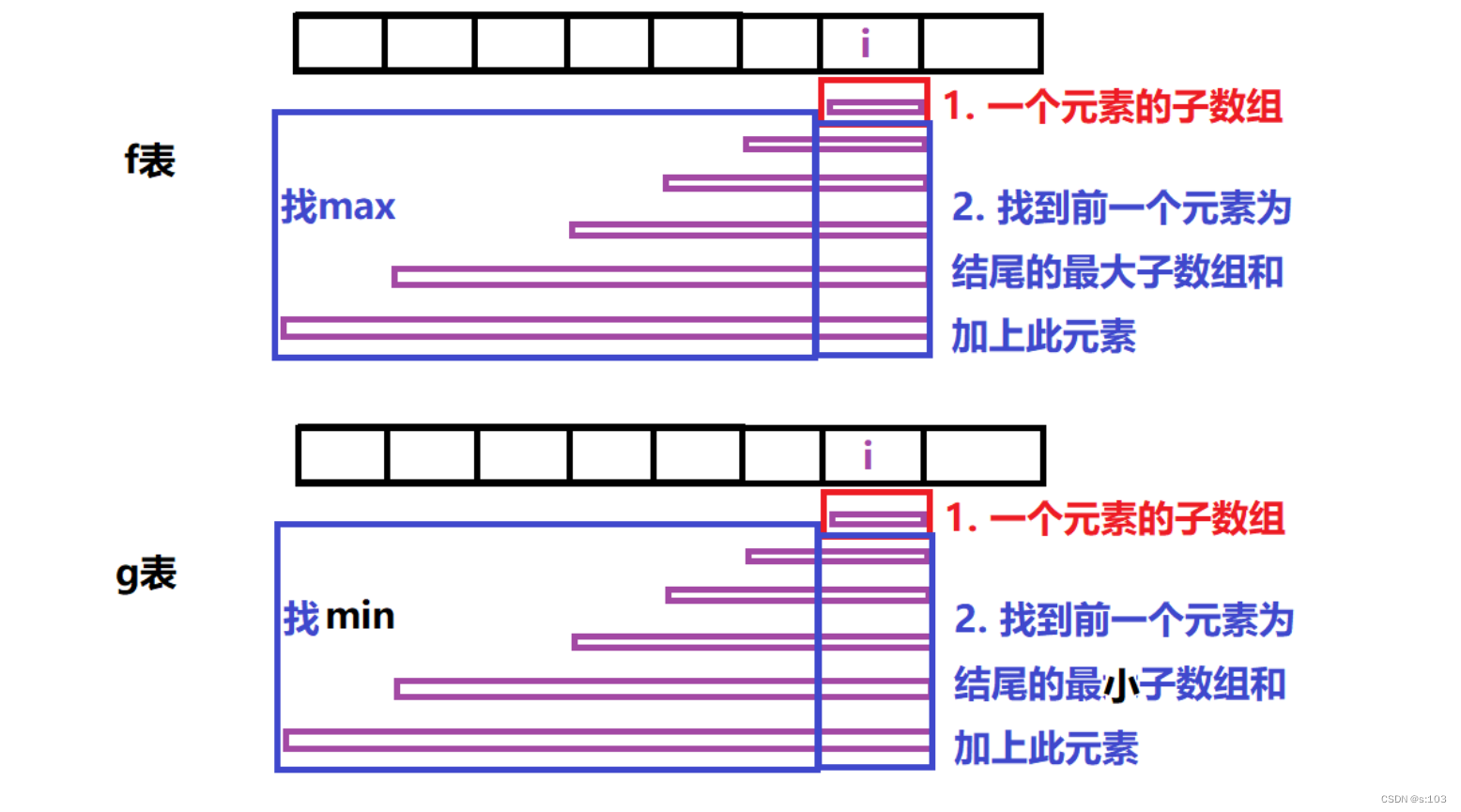
在这里插入图片描述

有：

f[i] = nums[i] + max{0, f[i - 1]}

g[i] = nums[i] + min{0, g[i - 1]}

2.2.3 初始化

虚拟节点法

  1. 不影响原dp值
  2. 下标对应问题

在这里插入图片描述

2.2.4 填表顺序

从左往右两个表一起填

2.2.5 返回值

在f表中找到最大值 => max{f[ ]} => 常规子数组的最大和

在g表中找到最小值 => sum - min{g[ ]} => 环形子数组的最大和

注意，还有一个细节！

  • 如果sum == min{g[ ]}，那么最大和就为0了？
  • 并不是，因为环形子数组也至少要有一个元素！所以这里应该是负无穷大
  • 这样则代表的是环形子数组无可能为最大和

3. 代码实现

class Solution {public int maxSubarraySumCircular(int[] nums) {//1. 创建dp表//2. 初始化//3. 填表//4. 返回值int n = nums.length;int[] f = new int[n + 1];int[] g = new int[n + 1];int max = Integer.MIN_VALUE;int min = Integer.MAX_VALUE;int sum = 0;for(int i = 1; i < n + 1; i++) {f[i] = Math.max(0, f[i - 1]) + nums[i - 1];g[i] = Math.min(0, g[i - 1]) + nums[i - 1];max = Math.max(max, f[i]);min = Math.min(min, g[i]);sum += nums[i - 1];}return sum == min ? max : Math.max(max, sum - min);}
}

在这里插入图片描述

  1. 下标对应！
  2. 特殊情况处理！

在这里插入图片描述

3. 乘积最大子数组

传送门：力扣152

题目：

在这里插入图片描述

3.1 题目解析

在这里插入图片描述

3.2 算法原理

3.2.1 状态表示

根据经验 + 题目要求，我们可以快速得到，一维dp表（大小为n），dp[i]代表以i为结尾的子数组的乘积最大值~

但是我们稍微想一想状态转移方程（这些步骤其实在做题过程中，是没有明显的分割的）

  • 如果nums[i]为负数，那么我们要得到dp[i]，用到dp[i - 1]（到i - 1的子数组的最大乘积），nums[i] * dp[i - 1]反而成为了最小值~

所以一个dp表是解决不了问题的！

刚才我们得到了最小值，那么反着看，如果我们要得到最大值，那么就需要前者的最小值

  • 则得出，我们是需要知道“乘积最小值”

故，演变成了多状态问题

f[i]代表i为结尾的子数组的乘积最大值

g[i]代表i为结尾的子数组的乘积最小值

3.2.2 状态转移方程

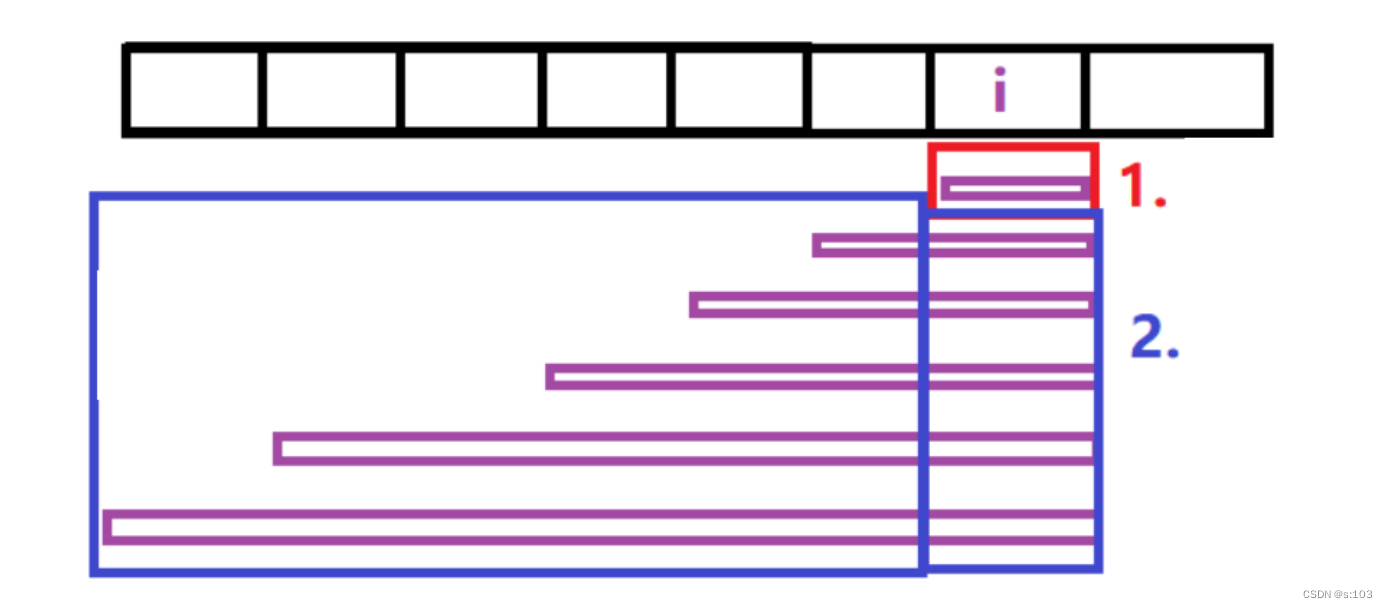
在这里插入图片描述

对于f表：

  1. 子数组大小为1，f[i] = nums[i];
  2. 子数组大小大于1
    1. nums[i] < 0, f[i] = nums[i] * g[i - 1]
    2. nums[i] > 0, f[i] = nums[i] * f[i - 1]（由于nums为整数数组，所以没有乘积后变小的情况）
    3. nums[i] == 0, f[i] = 0

对于g表：

  1. 子数组大小为1，g[i] = nums[i];
  2. 子数组大小大于1
    1. nums[i] < 0, g[i] = nums[i] * f[i - 1]
    2. nums[i] > 0, g[i] = nums[i] * g[i - 1]（由于nums为整数数组，所以没有乘积后变大的情况）
    3. nums[i] == 0, f[i] = 0

所以得到状态转移方程：

f[i] = max{nums[i], nums[i] * f[i - 1], nums[i] * g[i - 1]};

  • 0可以省去，因为有一个大于等于0的数

g[i] = min{nums[i], nums[i] * f[i - 1], nums[i] * g[i - 1]};

  • 0可以省去，因为有一个小于等于0的数

这样写就无需判断nums[i]正负~

3.2.3 初始化

虚拟节点法：

  1. 不影响原有值
  2. 下标对应问题

1乘以任何值都不会改变其值，所以两个表前添加一个1的节点即可

3.2.4 填表顺序

从左往右，两个表一起填

3.2.5 返回值

返回f表中的最大值（不包含虚拟节点）

3.3 编写代码

class Solution {public int maxProduct(int[] nums) {//1. 创建dp表//2. 初始化//3. 填表//4. 返回值int n = nums.length;int[] f = new int[n + 1];int[] g = new int[n + 1];f[0] = 1;g[0] = 1;int max = Integer.MIN_VALUE;for(int i = 1; i < n + 1; i++) {int number = nums[i - 1];f[i] = Math.max(number, Math.max(number * f[i - 1], number * g[i -1]));g[i] = Math.min(number, Math.min(number * f[i - 1], number * g[i -1]));max = Math.max(max, f[i]);}return max;}
}

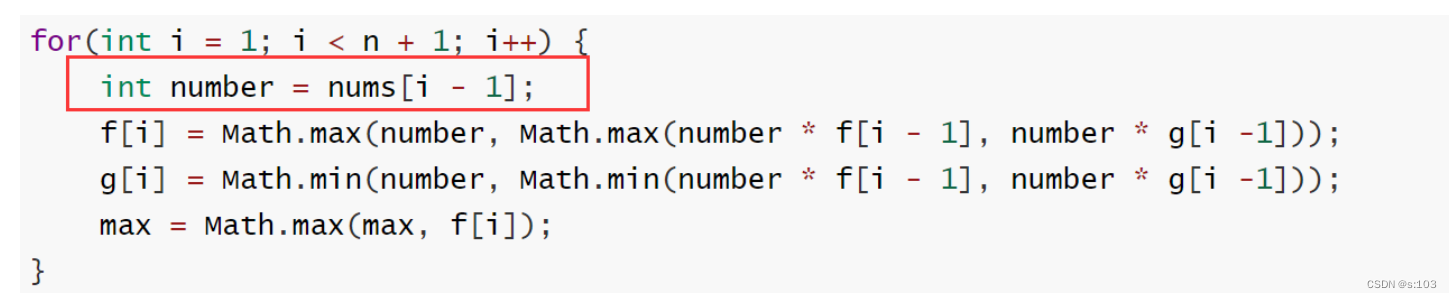
在这里插入图片描述

  • 注意下标对应！

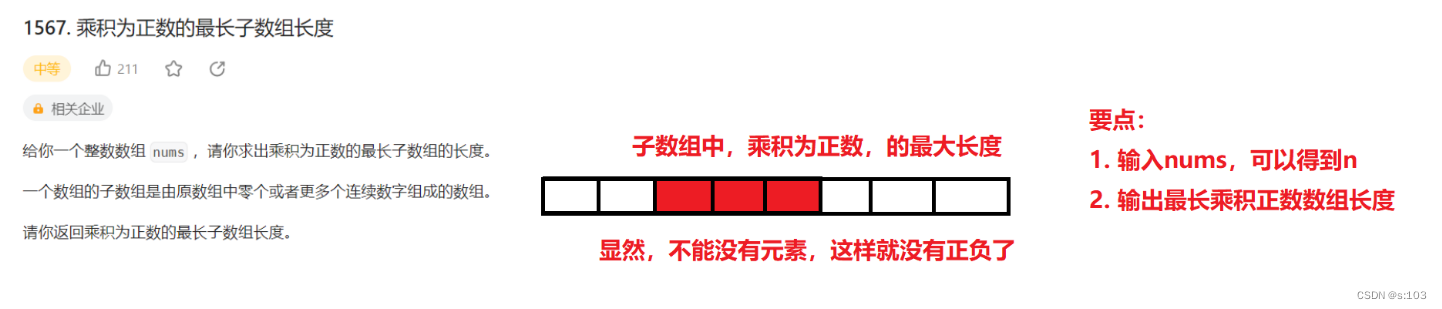
在这里插入图片描述

4. 乘积为整数的最长子数组长度

传送门：力扣1567

题目：

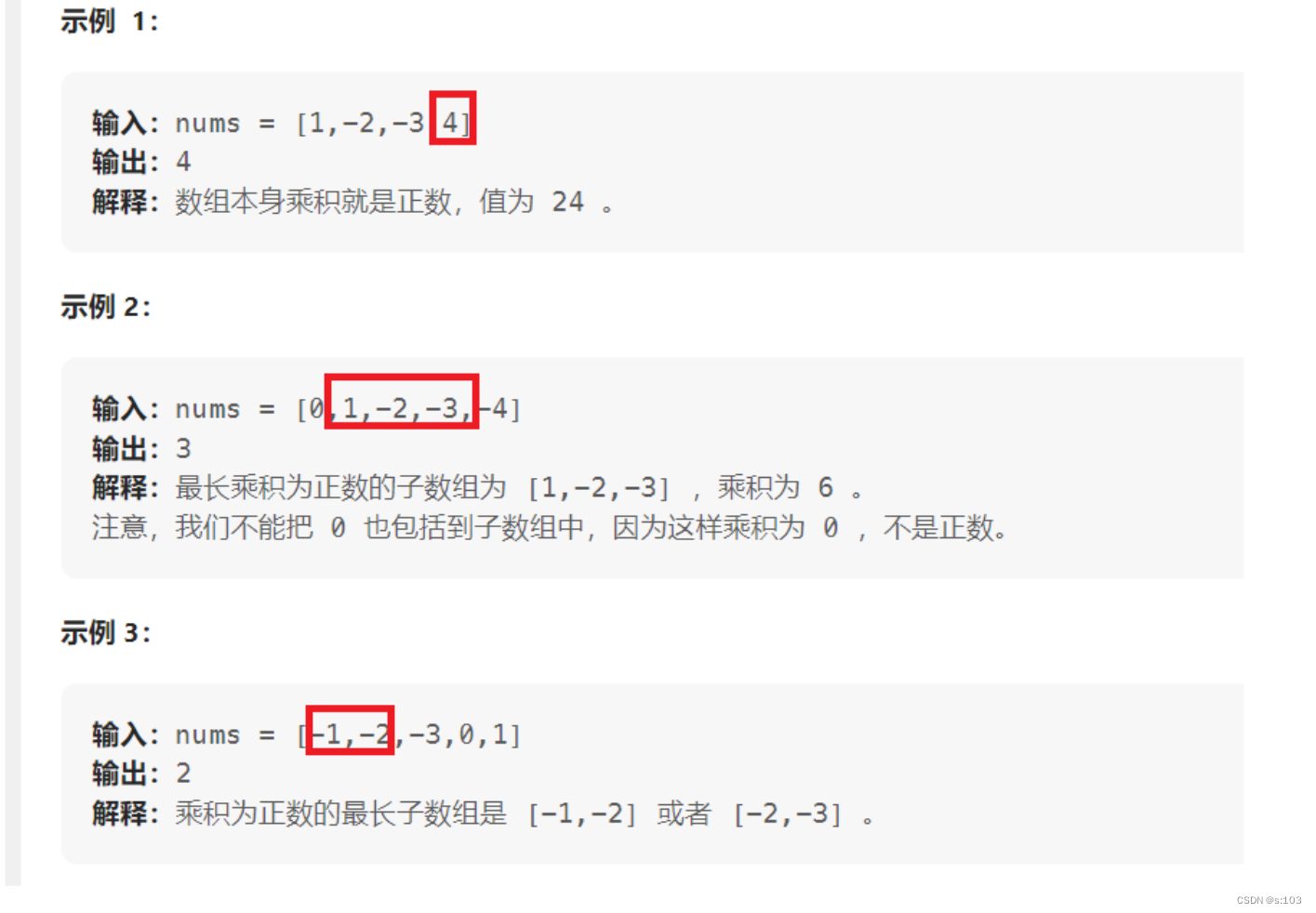
在这里插入图片描述

4.1 题目解析

在这里插入图片描述

在这里插入图片描述

4.2 算法原理

4.2.1 状态表示

根据“经验 + 题目要求”快速得到，一维dp表，大小为n，dp[i]代表“乘积正数子数组最长长度”

  • 同样的，如果只是正数的最长长度，是不能解决问题的，因为nums[i]小于0，dp[i]，无法用dp[i - 1]去表示！

而nums[i]小于0，我们需要“负数”去负负得正

  • 所以我们还需要“乘积负数子数组最长长度”

所以演变成多状态问题：

f[i]代表乘积正数子数组最长长度

g[i]代表乘积负数子数组最长长度

4.2.2 状态转移方程

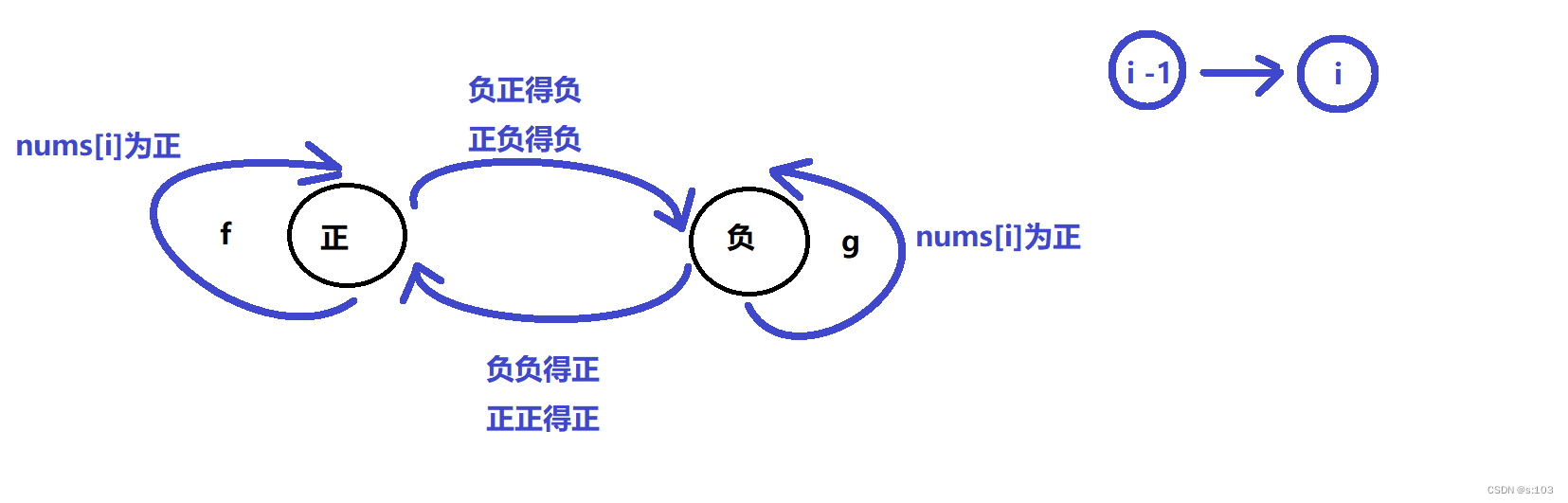
在这里插入图片描述

对于f表：

  1. 子数组长度为1
    1. nums[i] > 0, f[i] = 1
    2. nums[i] <= 0, f[i] = 0
  2. 子数组长度大于1
    1. nums[i] > 0, f[i] = 1 + f[i - 1]（正数延续）
    2. nums[i] < 0, f[i] = 1 + g[i - 1]（负负得正）
    3. nums[i] = 0, f[i] = 0

nums[i] = 0，前功尽弃~

细节：

nums[i] < 0, g[i - 1] == 0，则f[i] = 0！

对于g表：

  1. 子数组长度为1
    1. nums[i] < 0, g[i] = 1
    2. nums[i] >= 0, g[i] = 0
  2. 子数组长度大于1
    1. nums[i] > 0, g[i] = 1 + g[i - 1]（负数延续）
    2. nums[i] < 0, g[i] = 1 + f[i - 1]（正负得负）
    3. nums[i] = 0, g[i] = 0

nums[i] = 0，前功尽弃~

细节：

nums[i] > 0, g[i - 1] == 0，则g[i] = 0！

所以得到状态转移方程：

  1. nums[i] == 0时，f[i] = 0, g[i] = 0，java数组本身就是0~

  2. nums[i] < 0 时

    • f[i] = g[i - 1] == 0 ? 0 : 1 + g[i - 1]
    • g[i] = 1 + f[i - 1]

  3. nums[i] > 0时

    • f[i] = 1 + f[i - 1]
    • g[i] = g[i - 1] == 0 ? 0 : 1 + g[i - 1]

4.2.3 初始化

用假数据法，f表和g表前面加一个值为0的假节点

  1. 不影响原值
  2. 下标对应问题

4.2.4 填表顺序

从左往右，两个表一起填

4.2.5 返回值

f表最大值（不包含假节点）

4.3 代码实现

class Solution {public int getMaxLen(int[] nums) {//1. 创建dp表//2. 初始化//3. 填表//4. 返回值int n = nums.length;int[] f = new int[n + 1];int[] g = new int[n + 1];int max = 0;for(int i = 1; i < n + 1; i++) {if(nums[i - 1] > 0) {f[i] = 1 + f[i - 1];g[i] = g[i - 1] == 0 ? 0 : 1 + g[i - 1];}else if(nums[i - 1] < 0) {f[i] = g[i - 1] == 0 ? 0 : 1 + g[i - 1];g[i] = 1 + f[i - 1];}max = Math.max(max, f[i]);}return max;}
}

在这里插入图片描述

  • 注意下标对应！

在这里插入图片描述

文章到此结束！谢谢观看
可以叫我 小马，我可能写的不好或者有错误，但是一起加油鸭🦆！

代码位置：DP05 · 游离态/马拉圈2023年7月 - 码云 - 开源中国 (gitee.com)

还有下集~


http://www.ppmy.cn/news/696684.html

相关文章

Mdk4

Mdk4

攻击模式b&#xff1a;信标泛化 发送信标帧&#xff0c;在客户端显示假的AP。 这有时会使网络扫描器甚至是驱动程序崩溃 攻击模式a:拒绝认证服务 向在范围内发现的所有AP发送认证帧。 太多的客户可以冻结或重置几个AP。 攻击模式p:SSID探测和强制攻击 探测AP并检查回答&#…
阅读更多...
【HTML-5】小米耳机产品模块

【HTML-5】小米耳机产品模块

1. 以下为效果图 2.以下为源代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"…
阅读更多...
仿效小米商城静态页码html+css

仿效小米商城静态页码html+css

目录 一 实现效果 完整代码 1 HTML 2 CSS 一 实现效果 完整代码 1 HTML <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta …
阅读更多...
仿作小米商城页面

仿作小米商城页面

历时一周半的时间&#xff0c;终于在我的不懈努力下&#xff0c;完成了小米商城页面的静态仿作。真的&#xff0c;这个过程我觉得极其漫长&#xff0c;到最后也不敢相信自己能够完成。因为自己距上一次html和css的学习已经有好久了。好多好多的知识都已经忘记了&#xff0c;以至…
阅读更多...
小米官网页面（附带源码）

小米官网页面（附带源码）

https://gitee.com/panyi_blog/xiaomi-static-page-html-csshttps://gitee.com/panyi_blog/xiaomi-static-page-html-css 需要的小伙伴们可以去gitee上下载呀
阅读更多...
小米商品详情HTML +CSS +JS

小米商品详情HTML +CSS +JS

总体效果图展示&#xff1a; 中间内容展示&#xff1a; 大盒子套小盒子&#xff0c;进行css添加属性进行区分开来 HTML: CSS: 轮播图js代码&#xff1a; HTML: css:
阅读更多...
模拟静态小米商城官网html+css

模拟静态小米商城官网html+css

静态仿小米官网&#xff08;htmlcss&#xff09; 目录 项目结构页面截图部分功能完整代码下载 项目结构 mi.html 小米官网的首页 mi.css 小米官网首页样式表 base.css 公共样式表&#xff08;存放如clearfix&#xff0c;默认字体&#xff0c;和页面大小等代码&#xff09; f…
阅读更多...
使用HTML+CSS仿写小米官网首页

使用HTML+CSS仿写小米官网首页

通过学习&#xff0c;仅使用HTMLCSS仿写小米首页&#xff0c;以下是我的制作过程。 一.项目准备 1.使用sublime编辑器 2.下载素材 二.页面结构 三.效果图 四.具体实现 1&#xff09;.HTML部分 1.通过外链样式将创建好的 index.css文件导入到html文件中 <link rel"st…
阅读更多...
最新文章

Copyright @ 2022~2023