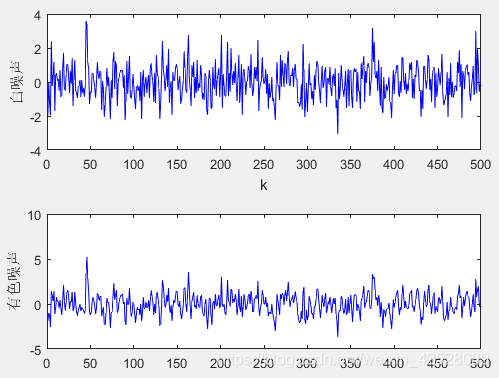
在论文去噪算法的比较过程中，我们通常加入高斯白噪声来模拟现实世界中的噪声。但是真实世界中属于有色噪声。

1： 白噪声  

      高斯白噪声是指信号的幅度分布服从高斯分布，而它的功率谱又是均匀分布的（是一个常数），从工程角度出发，一种噪声往往可视作具有有理谱密度的平稳随机过程，白噪声是一种最简单的随机过程，是由一些列不相关的随机变量组成的理想化随机过程。

2： 有色噪声：

    理想的白噪声是一种理论上的抽样，在物理上是很难实现的，但工程实际中测量的数据所包含的噪声都是有色噪声。所谓有色噪声就是说序列每一时刻都是相关的。

3： 两者的区别：

   （1）： 有定义可知，白噪声在不同时刻是不相关的，自相关函数为脉冲函数，有色噪声则是相关的。

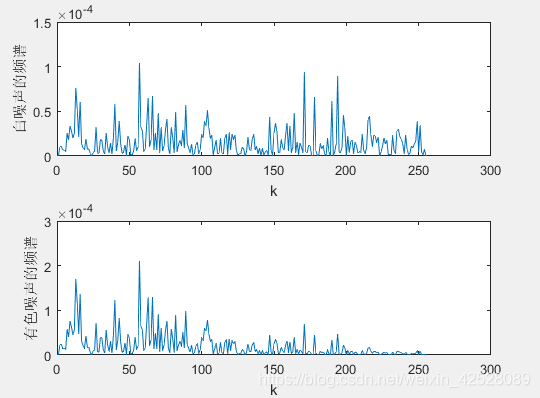
   （2）： 实际测试中可以通过测试功率谱来区分，白噪声的功率谱在各频率的指比较平均，有色噪声则会表现出明显的峰值。

 

N=500;MEAN=0;VAR=1;X=MEAN+VAR*randn(1,N);Y=zeros(1,N);
Y(1)=X(1);
for k=2:NY(k)=X(k)+0.5*X(k-1);
end[Fx fx]=myFFT(X',512);
Zx=1/N*Fx.*conj(Fx);[Fy fy]=myFFT(Y',512);
Zy=1/N*Fy.*conj(Fy);figure
subplot(2,1,1)
plot(X,'-b');
xlabel('k');
ylabel('白噪声')
subplot(2,1,2)
plot(Y,'-b','MarkerFace','g');
xlabel('k');
ylabel('有色噪声')figure
subplot(2,1,1);
plot(fx,Zx);
xlabel('k');
ylabel('白噪声的频谱')subplot(2,1,2);
plot(fy,Zy);
xlabel('k');
ylabel('有色噪声的频谱')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

运行结果：图1幅值  图2 频谱  图一的幅值不能明显识别。