0.前言
您好这里是limou3434的一篇博文,感兴趣可以看看我的其他内容。
排序算法简单理解就是:一串数组经过排序算法后得到有序的数组。排序算法在不同应用场景有不同的效果,因此我们有必要了解一些基础的排序算法。
而本次我给您带来的是一些基础的排序算法,主要涉及四种排序算法:插入排序、选择排序、交换排序、归并排序。
1.插入排序
1.1.直接插入排序
1.1.1.排序思想
在[0,end]有序的前提下,保证插入tmp后依旧有序。
1.1.2.具体code与test用例
#include <stdio.h>
void InsertSort(int* arr, int arrSize)
{for(int i = 0; i < arrSize; i++){int end = i-1;int tmp = arr[i];while (end >= 0){if (tmp < arr[end]){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}
void test(void)
{int arr[10];srand((unsigned)time(0));printf("排序前:");for (int i = 0; i < 10; i++){arr[i] = rand() % 10;printf("%d ", arr[i]);}printf("\n排序后:");InsertSort(arr, 10);for (int i = 0; i < 10; i++){printf("%d ", arr[i]);}
}
int main()
{test();return 0;
}
1.1.3.算法复杂度分析
在最坏情况下,每次tmp进来都需要把索引[0,end]的数据往后挪动,总共挪动的次数是“0+1+2+…+(n-1)=((0+n-1)*(n))/2”,即时间复杂度为O(n^2)。
1.2.希尔排序
1.2.1.排序思想
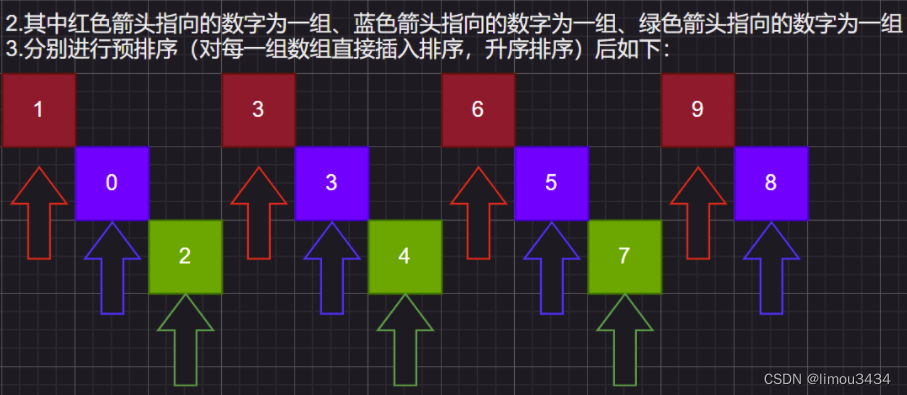
希尔排序的思想就是:先对数据进行预排序,然后进行直接插入排序。
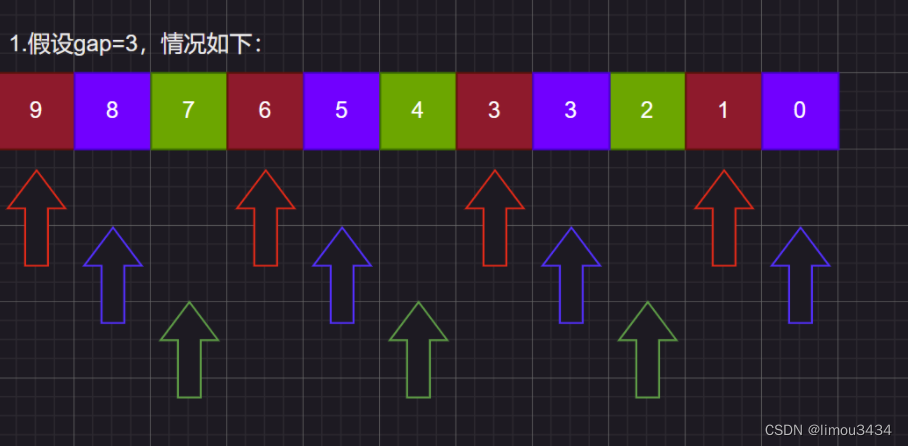
详细的思路就是:假设有一个值gap,将数据间隔gap分为一组,然后对每一组分别进行直接插入排序,因此这里可以复用之前的直接插入排序代码。
写希尔排序最好先写直接插入排序,然后改写为希尔排序(就是把1改成gap),最后得到预排序数组。

1.2.2.具体code与test用例
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <time.h>
#include <stdio.h>
#define SIZE 100
void InsertSort(int* arr, int arrSize)//插入排序的实现
{for (int i = 0; i < arrSize; i++){int end = i - 1;int tmp = arr[i];while (end >= 0){if (tmp < arr[end]){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}
void ShellSort(int* arr, int arrSize)//希尔排序的实现
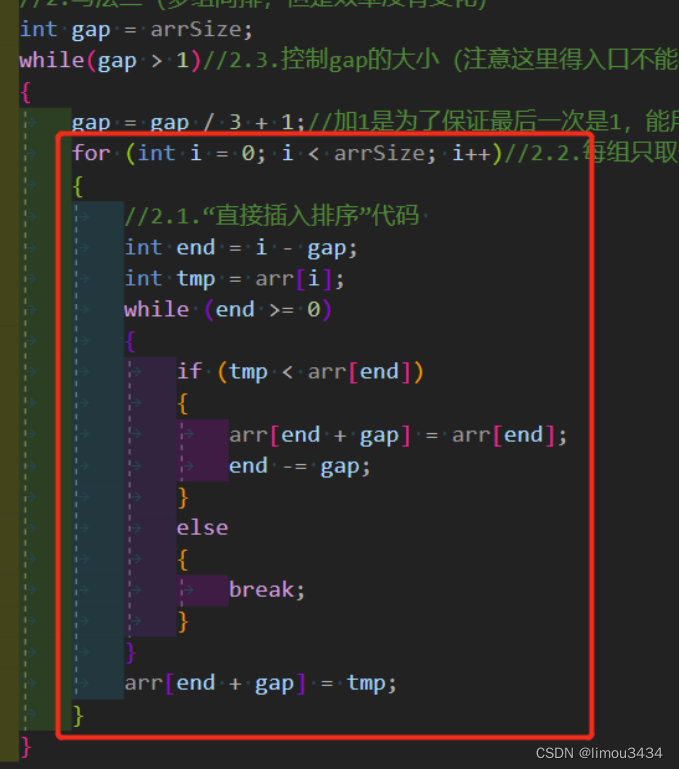
{//0.gap的最大意义在于:让最大的数更快跳到后面,让更小的数更快跳到前面//0.1.gap越大越不接近有序,但是跳得快//0.2.gap越小越接近有序,特别当gap=1时,其效果等价于直接插入排序//1.写法一(单组单排)//for (int gap = arrSize/2; gap >= 1; gap /= 2)//1.3.控制gap的大小//{// for (int j = 0; j < gap; j++)//1.2.分别使用“直接插入排序”排序gap组个数组// {// for (int i = j; i < arrSize; i += gap)// {// //1.1.某一次一组的“直接插入排序”// int end = i - gap;// int tmp = arr[i];// while (end >= 0)// {// if (tmp < arr[end])// {// arr[end + gap] = arr[end];// end -= gap;// }// else// {// break;// }// }// arr[end + gap] = tmp;// }// }//}//2.写法二(多组同排,但是效率没有变化)int gap = arrSize;while(gap > 1)//2.3.控制gap的大小(注意这里得入口不能写等于,会因为条件“gap=gap/3+1”而死循环,这是代码设计导致的){gap = gap / 3 + 1;//加1是为了保证最后一次是1,能用上gap=1的直接插入排序for (int i = 0; i < arrSize; i++)//2.2.每组只取一个元素排序{//2.1.“直接插入排序”代码 int end = i - gap;int tmp = arr[i];while (end >= 0){if (tmp < arr[end]){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}
}
void Test1()
{int arr[SIZE] = { 0 };for (int i = 0; i < SIZE; i++){arr[i] = rand() % 10;}for (int i = 0; i < SIZE; i++){printf("%d ", arr[i]);}printf("\n");printf("InsertSort() :");InsertSort(arr, SIZE);for (int i = 0; i < SIZE; i++){printf("%d ", arr[i]);}printf("\n\n");
}
void Test2()
{int arr[SIZE] = { 0 };for (int i = 0; i < SIZE; i++){arr[i] = rand() % 10;}for (int i = 0; i < SIZE; i++){printf("%d ", arr[i]);}printf("\n");printf("ShellSort() :");ShellSort(arr, SIZE);for (int i = 0; i < SIZE; i++){printf("%d ", arr[i]);}printf("\n\n");
}
int main()
{Test1();Test2();return 0;
}
1.2.3.算法复杂度分析
希尔排序的算法复杂度分析不能只看for循环,这是极其错误的,一个典型的例子就是:我们在写希尔排序的时候,写了“四层循环”和“三层循环”的方法,但是两种方法的效果是一样的。
以博主的数学知识是没有办法进行计算的(貌似在数学界也有些问题没有被解决),所以暂时跳过吧。我们只需要记住希尔排序的时间复杂度范围在[O(N*(log(2)(N))2),O(N2)]之间即可,整体认为希尔排序的时间复杂度是O(N^1.3)即可。
2.选择排序
2.1.直接选择排序
2.1.1.排序思想
从一个待排序列中选出最小/最大的数,然后将最小/最大的数和待排序列中的第一个数/最后一个数交换,不断重复。
但是这样效率太低,可以优化一下:从一个待排序列中选出最小的数和最大的数,然后将最小的数和最大的数分别和待排序列中的第一个数和最后一个数交换,不断重复,效率好了一倍。
2.1.2.具体code与test样例
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <time.h>
#include <stdio.h>
#define SIZE 10
void _Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}
void SelectSort(int* arr, int arrSize)
{int begin = 0, end = arrSize - 1;while (begin < end){int maxi = begin;int mini = end;for (int i = begin; i <= end; i++){if (arr[i] > arr[maxi])//选出最大数的下标{maxi = i;}if (arr[i] < arr[mini])//选出最小数的下标{mini = i;}}_Swap(&arr[begin], &arr[mini]);if (begin == maxi)//处理特殊情况{maxi = mini;}_Swap(&arr[end], &arr[maxi]);begin++;end--;}
}
int main()
{int arr[SIZE] = { 0 };for (int i = 0; i < SIZE; i++){arr[i] = rand() % 10;}for (int i = 0; i < SIZE; i++){printf("%d ", arr[i]);}printf("\n");printf("SelectSort() :");SelectSort(arr, SIZE);for (int i = 0; i < SIZE; i++){printf("%d ", arr[i]);}printf("\n\n");return 0;
}