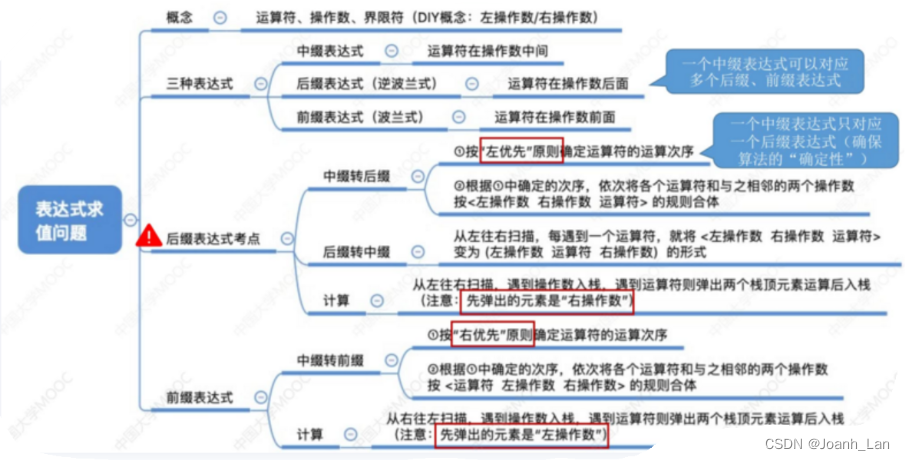
数据结构–栈的引用–前中后缀表达式(前部分)
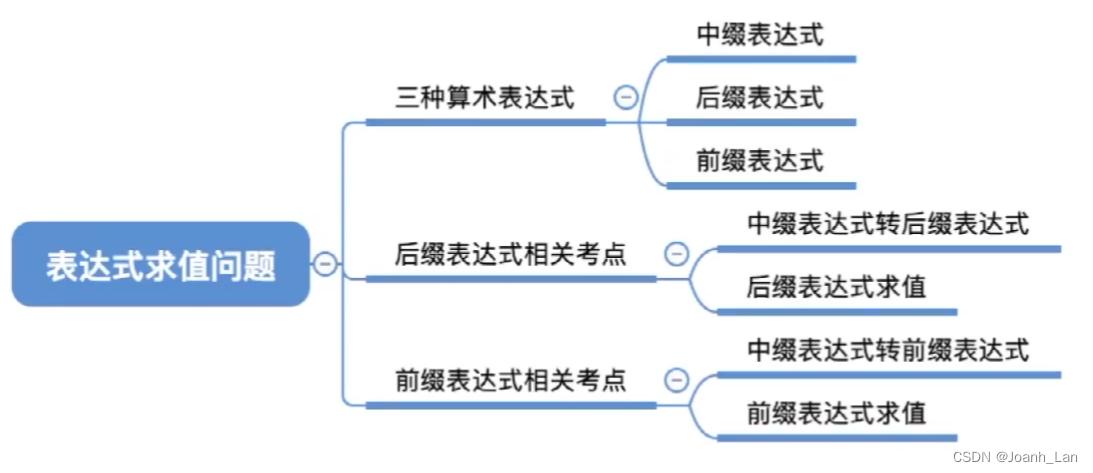
常见的算数表达式

由三个部分组成: 操作数、运算符、界限符 \color{red}操作数、运算符、界限符 操作数、运算符、界限符
ps:界限符是必不可少的,反映了计算的先后顺序
波兰表达式(让计算机更容易识别的算数表达式)
Reverse Polish notation(逆波兰表达式=后缀表达式)
Polish notation(波兰表达式=前缀表达式)
中缀 \color{red}中缀 中缀表达式:
运算符在两个操作数中间
a+b
a +b - c
a+b - c * d
后缀 \color{red}后缀 后缀表达式:
规则:运算符在两个操作数后面
a b +
a b+ c-
a b +cd *-
前缀 \color{red}前缀 前缀表达式:
规则:运算符在两个操作数前面
+a b
-+a b c
-+a b * c d
后缀表达式
后缀表达式的计算(手算)
中缀转后缀 \color{red}中缀转后缀 中缀转后缀的 手算方法 \color{green}手算方法 手算方法:
①确定中缀表达式中 各个运算符的运算顺序 \color{red}各个运算符的运算顺序 各个运算符的运算顺序
②选择下一个运算符,按照 「左操作数右操作数运算符」 \color{purple}「左操作数右操作数运算符」 「左操作数右操作数运算符」的方式组合成一个新的操作数
③如果还有运算符没被处理,就继续②

我们发现对于同一个中缀表达式按这个方法可能会有多个后缀表达式
原因:
运算顺序不唯一,因此对应的后缀表达式也不唯一
一:
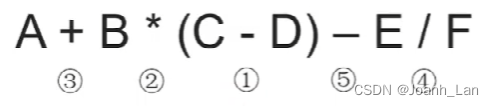

二:
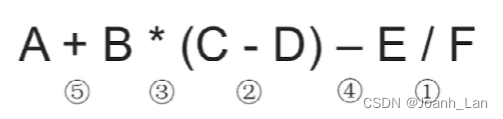
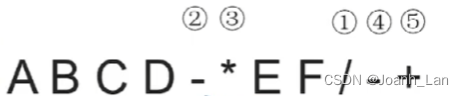
客观来看两种都正确,只是“机算”结果是前者
所以我们可以规定一个原则:
“左优先”原则 \color{red}“左优先”原则 “左优先”原则,这样可以保证结果的唯一性

后缀表达式的手算方法:
从左往右扫描,每遇到一个运算符,就让 运算符前面最近的两个操作数 \color{red}运算符前面最近的两个操作数 运算符前面最近的两个操作数执行对应运算, 合体为一个操作数 \color{red}合体为一个操作数 合体为一个操作数
注意:两个操作数的左右顺序

特点:
最后出现的操作数先被运算
LIFO(后进先出) → \to → 栈
后缀表达式的计算(机算)
用栈实现后缀表达式的计算:
①从左往右扫描下一个元素,直到处理完所有元素②若扫描到操作数则压入栈,并回到①;否则执③
③若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶,回到①
注意:先出栈的是“右操作数” \color{pink}注意:先出栈的是“右操作数” 注意:先出栈的是“右操作数”
若表达式合法 , 则最后栈中只会留下一个元素,就是最终结果 \color{pink}若表达式合法,则最后栈中只会留下一个元素,就是最终结果 若表达式合法,则最后栈中只会留下一个元素,就是最终结果
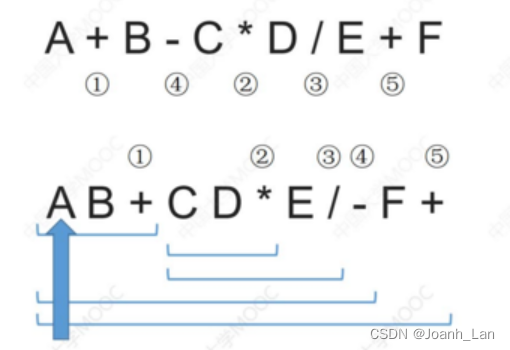
根据给定的中缀表达式"AB+CD*E/-F+",我们可以逐步生成后缀表达式,并记录每一步栈的情况。下面是每一步的栈情况:
- 初始时,栈为空。
- 遇到’A’,将其入栈。栈:A
- 遇到’B’,将其入栈。栈:AB
- 遇到’+‘,由于栈顶是运算符’+',优先级相同,所以将栈顶元素出栈并加入后缀表达式中。栈:A,后缀表达式:AB+
- 遇到’C’,将其入栈。栈:AC,后缀表达式:AB+
- 遇到’D’,将其入栈。栈:ACD,后缀表达式:AB+
- 遇到’‘,由于栈顶是运算符’‘,优先级高于’',所以将栈顶元素出栈并加入后缀表达式中。栈:AC,后缀表达式:AB+CD
- 遇到’E’,将其入栈。栈:ACE,后缀表达式:AB+CD*
- 遇到’/‘,由于栈顶是运算符’‘,优先级高于’/',所以将栈顶元素出栈并加入后缀表达式中。栈:AC,后缀表达式:AB+CDE/
- 遇到’-‘,由于栈顶是运算符’/‘,优先级低于’-‘,所以将’-'入栈。栈:AC-,后缀表达式:AB+CD*E/
- 遇到’F’,将其入栈。栈:AC-F,后缀表达式:AB+CD*E/
- 遇到’+‘,由于栈顶是运算符’-',优先级相同,所以将栈顶元素出栈并加入后缀表达式中。栈:AC,后缀表达式:AB+CD*E/-F+
- 遍历完中缀表达式,将栈中剩余的运算符全部出栈并加入后缀表达式中。栈:空,后缀表达式:AB+CD*E/-F+
最终得到的后缀表达式为"AB+CD*E/-F+",栈为空。
注意:上述过程中,我们使用了一个栈来辅助转换为后缀表达式。当遇到运算符时,我们需要判断栈顶元素与当前运算符的优先级,根据优先级决定是否出栈并加入后缀表达式中。
前缀表达式
中缀表达式转前缀表达式(手算)
中缀转前缀的手算方法:
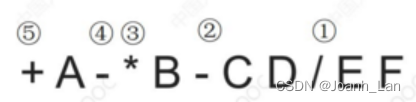
①确定中缀表达式中 各个运算符的运算顺序 \color{red}各个运算符的运算顺序 各个运算符的运算顺序
②选择下一个运算符,按照 「运算符左操作数右操作数」 \color{red}「运算符左操作数右操作数」 「运算符左操作数右操作数」的方式组合成一个新的操作数
③如果还有运算符没被处理,就继续②
“右优先”原则 \color{red}“右优先”原则 “右优先”原则:只要右边的运算符能先计算,就优先算 右边 \color{red}右边 右边的

中缀表达式转前缀表达式(计算)
用栈实现前缀表达式的计算:
① 从右往左 \color{red}从右往左 从右往左扫描下一个元素,直到处理完所有元素
注意 : 先出栈的是“左操作数” \color{pink}注意:先出栈的是“左操作数” 注意:先出栈的是“左操作数”
②若扫描到操作数则压入栈,并回到①;否则执行③
③若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶,回到①
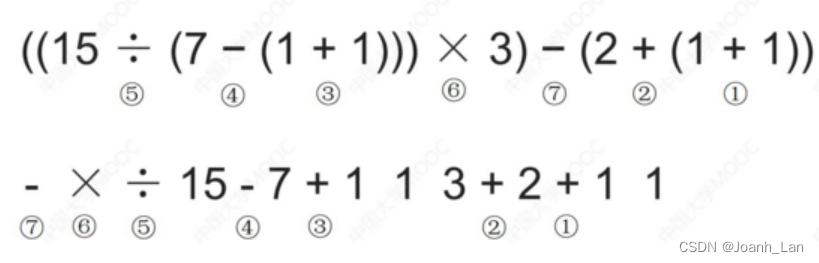
首先,我们需要理解前缀表达式的计算过程。前缀表达式是一种将运算符放在操作数之前的表达式表示方法。计算前缀表达式时,我们从右到左遍历表达式,遇到操作数则将其入栈,遇到运算符则从栈中取出两个操作数进行运算,并将运算结果再次入栈。最后,栈中只剩下一个结果,即为表达式的计算结果。
根据题目给出的前缀表达式:/ 15 -7 + 1 1 3 + 2 + 1 1
我们按照计算过程来模拟每一步栈的情况:
- 遇到15,入栈:[15]
- 遇到-7,入栈:[-7, 15]
- 遇到+,从栈中取出两个操作数-7和15,计算结果为8,将结果入栈:[8]
- 遇到1,入栈:[1, 8]
- 遇到1,入栈:[1, 1, 8]
- 遇到3,入栈:[3, 1, 1, 8]
- 遇到+,从栈中取出两个操作数3和1,计算结果为4,将结果入栈:[4, 1, 8]
- 遇到2,入栈:[2, 4, 1, 8]
- 遇到+,从栈中取出两个操作数2和4,计算结果为6,将结果入栈:[6, 1, 8]
- 遇到1,入栈:[1, 6, 1, 8]
- 遇到1,入栈:[1, 1, 6, 1, 8]
- 遇到+,从栈中取出两个操作数1和1,计算结果为2,将结果入栈:[2, 6, 1, 8]
- 遇到/,从栈中取出两个操作数2和6,计算结果为3,将结果入栈:[3, 1, 8]
- 遇到+,从栈中取出两个操作数3和1,计算结果为4,将结果入栈:[4, 8]
- 遇到/,从栈中取出两个操作数4和8,计算结果为0.5,将结果入栈:[0.5]
最终栈中只剩下一个结果0.5,即为表达式的计算结果。
每一步栈的情况如下:
- [15]
- [-7, 15]
- [8]
- [1, 8]
- [1, 1, 8]
- [3, 1, 1, 8]
- [4, 1, 8]
- [2, 4, 1, 8]
- [6, 1, 8]
- [1, 6, 1, 8]
- [1, 1, 6, 1, 8]
- [2, 6, 1, 8]
- [3, 1, 8]
- [4, 8]
- [0.5]
知识点回顾与重要考点