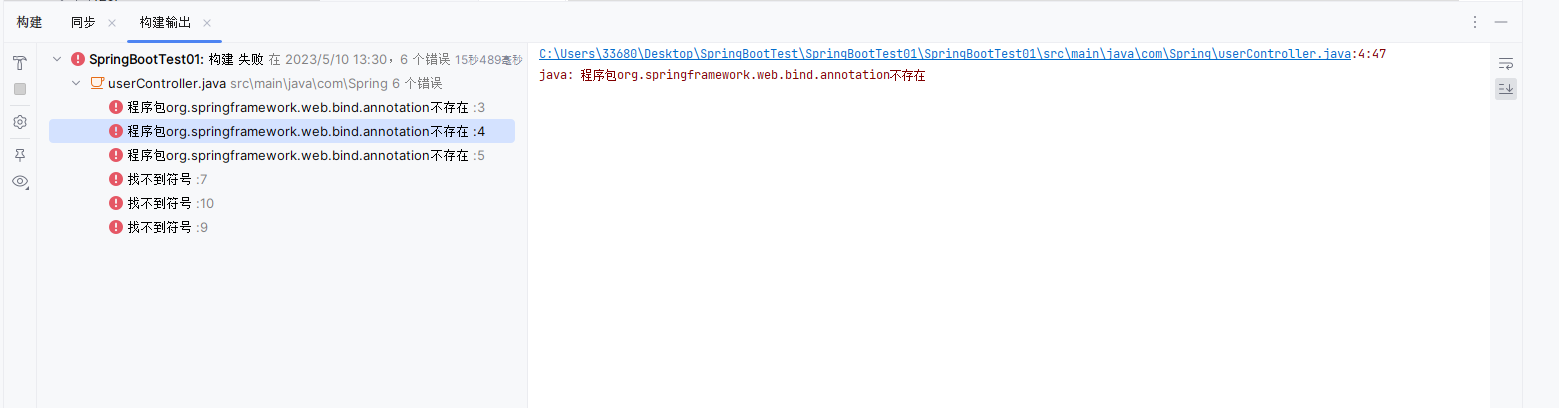
前置知识
欧拉函数 ϕ ( n ) \phi(n) ϕ(n)
欧拉函数简介
阶
若 g g g和 n n n互质,则令 g x % n = 1 g^x\%n=1 gx%n=1的最小正整数 x x x称为 g g g模 n n n的阶。
原根
对于互质的两个正整数 g g g和 n n n,如果 g g g模 n n n的阶为 ϕ ( n ) \phi(n) ϕ(n),则称 g g g为 n n n的原根。
求原根
一般的原根都比较小,暴力枚举即可。
离散对数
设 g g g为 m m m的原根,则当
g k ≡ x ( m o d m ) g^{k}\equiv x\pmod m gk≡x(modm)
时,有
Ind g x ≡ k ( m o d ϕ ( m ) ) \text{Ind}_gx\equiv k\pmod{\phi(m)} Indgx≡k(modϕ(m))
而且能保证 ∀ x ∈ [ 1 , m − 1 ] \forall x\in[1,m-1] ∀x∈[1,m−1],都存在 k ∈ [ 1 , m − 1 ] k\in[1,m-1] k∈[1,m−1]使得 g k = x g^k=x gk=x。
证明
若 ∃ x ∈ [ 1 , m − 1 ] \exist x\in[1,m-1] ∃x∈[1,m−1],不存在 k k k使得 g k = x g^k=x gk=x
则 ∃ y ∈ [ 1 , m − 1 ] \exist y\in[1,m-1] ∃y∈[1,m−1],存在至少两个 k ∈ [ 1 , m − 1 ] k\in[1,m-1] k∈[1,m−1]使得 g k = y g^k=y gk=y
设满足条件的 k k k中不同的两个为 k 1 k_1 k1和 k 2 k_2 k2且 k 1 < k 2 k_1<k_2 k1<k2
则 g k 1 ≡ g k 2 ( m o d m ) g^{k_1}\equiv g^{k_2}\pmod m gk1≡gk2(modm)
得 g k 2 − k 1 ≡ 1 ( m o d m ) g^{k_2-k_1}\equiv 1\pmod m gk2−k1≡1(modm)
所以 g g g不为 m m m的原根,矛盾
由此即可得证
离散对数的性质
离散对数的性质与对数函数的性质相似
Ind g ( x y ) = Ind g ( x ) + Ind g ( y ) ( m o d ϕ ( m ) ) \text{Ind}_g(xy)=\text{Ind}_g(x)+\text{Ind}_g(y)\pmod{\phi(m)} Indg(xy)=Indg(x)+Indg(y)(modϕ(m))
Ind g ( x y ) = y ⋅ Ind g ( x ) ( m o d ϕ ( m ) ) \text{Ind}_g(x^y)=y\cdot \text{Ind}_g(x)\pmod{\phi(m)} Indg(xy)=y⋅Indg(x)(modϕ(m))
离散对数的作用
可以将模 m m m意义下的乘法转换为模 ϕ ( m ) \phi(m) ϕ(m)意义下的加法,从而更方便地解决问题。
code
int find(int e){for(int i=2;i<=e;i++){for(int j=1,l=i;j<=e;j++,l=l*i%e){if(l==1){if(j==e-1) return i;break;}}}
}//找原根
void init(){int gt=find(m);for(int i=0,l=1;i<m-1;i++){ind[l]=i;l=l*gt%m;}
}//求离散对数