原文地址:
BWT (Burrows–Wheeler_transform)数据转换算法
原文讲解十分详细,但关键地方有点绕,故作分析注释
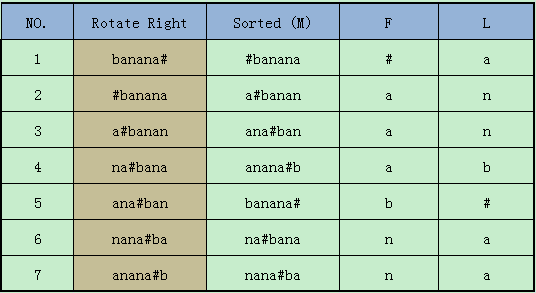
因为进行的是循环移位,且是循环左移注意下面的性质:
1、L的第一个元素是Text中的最后一个元素
2、对于M中的每一行(第一行除外)第一个元素都是最后一个元素的下一个元素。
也就是说,对于文本块而言,同一行中F是L的下一个元素,L是F的前一个元素。
这里就是说:F列和L列,相同次序的元素,是相邻关系
具体是:相同次序时,L列的元素是F列的前一个
例如:
F[1] == ‘#’ L[1] == ‘a’ , ‘a’在’#’的前面(循环来看)
F[5] == ‘b’ L[5] == ‘#’ , ‘#’在’b’的前面
这样,就需要
(1)通过”F”列中的元素,找到他前面的字符,就是对应的同一行“L”列;
因为F列是按字母序排列的,而我们的标记字符“#”又小于所有的文本字符,所以:F[1]一定是我们的标记字符“#”
这样,根据上面的结论:相同次序时,L列的元素是F列的前一个,可以得到:L[1] == ‘a’就是原字符串的最后一个字符
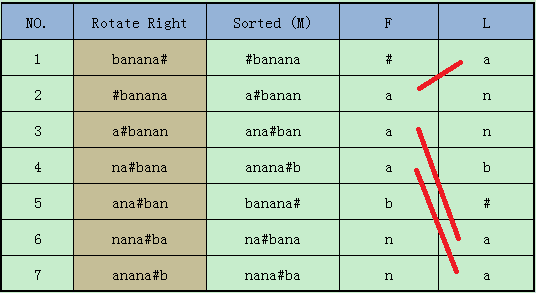
(2)通过“L”列中的元素,找到他在“F”列中的对应字符位置。但是“L”中有3个字符a,如何对应F中的3个a呢?因为L是F的前一个元素,多个具有相同前缀的字符串排序,去掉共同前缀后相对次序没有变化。所有遇到多个相同的字符,相对位置不变;
上一步我们找到了原字符串的最后一个字符,就是L[1] == ‘a’,那么下一步呢?
既然我们刚刚根据字符串的第一个字符找到了它的前一个字符(通过“#”找到了“a”),那么我们就可以继续找“a”的前一个字符,如此重复,就完成了解码的任务。
如何找“a”的前一个字符?还是继续利用我们最开始的结论:相同次序时,L列的元素是F列的前一个,只要找到“a”在F列中的位置x,就可以知道“a”的前一个元素为L[x]
但问题是,F中有多个“a”,如何确定哪一个“a”对应的是我们现在的“a”?
即:是否可以找到 L和F中重复元素的对应关系
这句话很关键:
因为L是F的前一个元素,多个具有相同前缀的字符串排序,去掉共同前缀后相对次序没有变化。
先来看L列的排列方式。
因为我们知道:相同次序时,L列的元素是F列的前一个 (又是这个),而F列是循环右移得到的字符串,按字母序排列后,每个串的第一个字母。
换句话说就是:
L列按每个元素后面的字符串的字母序排列再来看F列的排列方式。
F列按字母序排列,而我们可以把字母序排列这样描述:- 当首字母不同时,按首字母的字母序排列;
- 当首字母相同时,按后面的字符串的字母序排列
这里我们就能发现,当首字母相同时,为得到L列和F列而使用的排列方式是相同的,而首字母相同就是L列和F列中的重复元素。
换句话说,我们把L列中的“a”和F列中的“a”按从前往后或者从后往前的顺序取出,他们本就是一一对应的。
整个解码的问题到这里就结束了。